SGD（Stochastic Gradient Descent）的损失函数（Loss Function）

最新推荐文章于 2024-11-23 18:12:29 发布
翻译 最新推荐文章于 2024-11-23 18:12:29 发布 · 2.5k 阅读 · 1

博客介绍了二分类的损失函数，还提及sklearn中的随机梯度下降。随机梯度下降是一种以随机方式最小化损失函数的优化技术，逐样本进行梯度下降步骤，是拟合线性模型的高效方法。

二分类的损失函数

sklearn：

Stochastic Gradient Descent is an optimization technique which minimizes a loss function in a stochastic fashion, performing a gradient descent step sample by sample. In particular, it is a very efficient method to fit linear models.

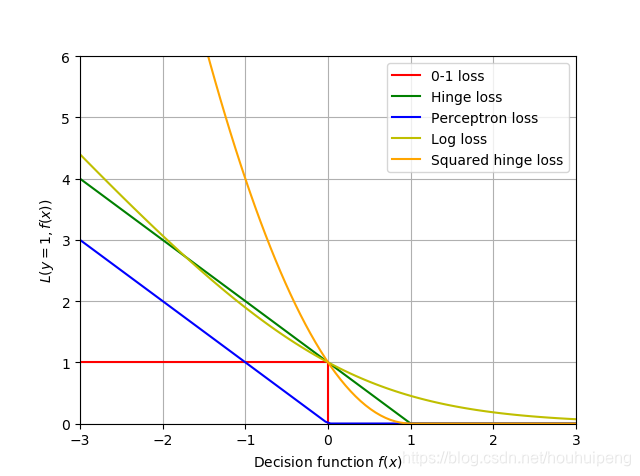
在这里插入图片描述

Stochastic Gradient Descent (SGD)原理与代码实例讲解
AI天才研究院
06-16 1019
SGD作为一种经典的优化算法，已经在机器学习和深度学习领域取得了广泛应用。然而，随着数据规模和模型复杂度的不断增加，SGD也面临着新的挑战。未来，如何进一步提高SGD的收敛速度和稳定性，如何在大规模分布式系统中高效实现SGD，将是研究的重点方向。
随机梯度下降 (Stochastic Gradient Descent)
AI天才研究院
06-18 1437
1. 背景介绍 在机器学习和深度学习中，优化算法是非常重要的一部分，它们用于找到最优的模型参数，以最小化损失函数。随机梯度下降（Stochastic Gradient Descent，SGD）是一种常用的优化算法，它通过随机选择数据样本的梯度来更新模型参数，因此得名。在这篇文章中，我们将深入探讨随机梯度下降的原理、实现和应用。
梯度下降优化算法综述（翻译）
热门推荐
自然语言处理大菜鸟--HsingWang
03-24 1万+
原文链接：http://sebastianruder.com/optimizing-gradient-descent 博文地址： 梯度下降是最流行的优化算法之一并且目前为止是优化神经网络最常见的算法。与此同时，每一个先进的深度学习库都包含各种算法实现的梯度下降（比如lasagne's, caffe's, 和 keras'的文档）。然而，这些算法经常作为黑盒优化程序使用，所以难以感受
SGD
bigheadmonkey的博客
05-02 417
随机梯度下降（stochastic gradient descent，SGD） 当样本数据过于庞大时，采用原来传统的梯度下降算法，训练时间过长，收敛太慢，所以使用SGD的方法来加快收敛，该方法伪代码如下： 每个参数更新时只使用一个样本，原先是使用所有样本，这样说来，该算法虽然大概率得不到全局最优解，但是当样本数量足够多时，总是能得到最优解附近的值，而且训练速度快。 后续在深度学习中广泛使用的mini-bach，每次更新参数使用几百个样本，这样做比使用一个样本大概率训练效果好些，而且训练速度也较快。伪代码如
sigmoid、softmax函数/交叉熵损失函数/二分类、多分类详细推导过程
PuJiang-的博客
08-23 3291
交叉熵损失函数、MSE、二分类、多分类
Python深度学习——机器学习基础
方寸想法，编码宇宙
04-29 434
文章目录机器学习的四个分支1.监督学习2.无监督学习3.自监督学习4.强化学习评估机器学习模型1.训练集、验证集和测试集2.评估模型的注意事项3.数据预处理、特征工程和特征学习（1）神经网络的数据预处理（2）特征工程 机器学习的四个分支 1.监督学习 监督学习是目前最常见的机器学习类型。给定一组样本（通常由人工标注），它可以学会将输入数据映射到已知目标［也叫标注（annotation）］。一般来说...
损失函数(Loss Function) -1
huhu0769的博客
01-29 793
损失函数(Loss Function) -1 http://www.ics.uci.edu/~dramanan/teaching/ics273a_winter08/lectures/lecture14.pdf Loss Function 损失函数可以看做 误差部分(loss term) + 正则化部分(regularization term) 1
随机梯度下降 Stochastic Gradient Descent (SGD) 原理与代码实战案例讲解
AI天才研究院
08-05 1651
随机梯度下降(Stochastic Gradient Descent, SGD)作为机器学习和深度学习中最常用的优化算法之一,在训练大规模数据集和复杂模型时展现出卓越的性能。本文将深入探讨SGD的原理,阐述其数学模型,并通过代码实例和实际应用场景来帮助读者全面理解和掌握这一重要算法。Momentum:引入动量项,加速SGD收敛并减少震荡Adagrad:自适应学习率,为每个参数维护一个学习率RMSprop:解决Adagrad学习率过度衰减的问题。
【人工智能专栏】Stochastic Gradient Descent (SGD) 随机梯度下降
热情、奔放、快乐编程！
08-06 289
SGD 实际上就是在一个 epoch 中每个 batch 做一次梯度更新，因为数据集每个 epoch 会被打乱，于是就相当于是随机样本子集对模型进行权值更新。
【小知识】神经网络中的SGD优化器和MSE损失函数
weixin_43728604的博客
10-27 2531
今天来讲下之前发的一篇极其简单的搭建网络的博客里的一些细节（前文传送门） 之前的那个文章中，用Pytorch搭建优化器的代码如下： # 设置优化器 optimzer = torch.optim.SGD(myNet.parameters(), lr=0.05) loss_func = nn.MSELoss() 那么其中的额SGD和MSE究竟是什么呢？ 一、SGD方法 我们要想训练我们的神经网络，就...
各种梯度优化算法介绍（SGD Loss剧烈波动）
ice_martin的博客
08-12 1003
原文地址
损失函数及梯度下降
carakia的博客
10-18 828
https://blog.youkuaiyun.com/wearge/article/details/77073142
CS231n-2017 第3讲 损失函数与优化
suredied的博客
08-30 720
一. 损失函数 1. 基本概念 为了评估现有的模型的好坏，需要一个定量指标。这就是损失函数起作用之处。 对于由NNN个样本组成的数据集{(xi,yi)}Ni=1{(xi,yi)}i=1N\{(x_i, y_i)\}_{i=1}^N，定义总体损失函数为各个样本造成的损失的平均 L=1N∑iLi(f(xi,W),yi)L=1N∑iLi(f(xi,W),yi) L = \frac{1}{...
损失函数和优化算法
zjs246813的博客
11-23 1284
损失函数可以用来衡量模型拟合程度，通过计算模型预测的输出与实际标签之间的差异可以获得一个损失值，然后。假设该损失函数只涉及一个自变量w，易于求得该损失函数的梯度得到一个较佳的损失值。，即损失函数对参数w的偏导，同理参数b也可以这样求导，最后计算出损失函数的梯度。而实际中，一个损失函数涉及大量自变量（参数），直接求偏导太复杂，可以根据。，然后求损失函数对自变量w、b的偏导，这里以求对w的偏导为例。是损失函数的两个自变量，函数训练得到的两个参数。是训练后得到的函数，然后定义损失函数。最后一层即输出层，计算。
机器学习损失函数 / 激活函数 / 优化算法 总览
noobiee的博客
08-26 2870
关键词：交叉熵，KL散度（相对熵），BCELoss，Contrastive loss，triplet loss，n-pair loss，focal loss sigmoid，tanh，ReLU，PReLU，ELU，GeLU BGD，SGD，momentum，NAG，AdaGrad，RMSprop，Adam，AdamW
C++线性回归（SGD、BGD、MBGD）
weixin_38442390的博客
12-08 639
代码 #include<iostream> #include<random> using namespace std; double w = 0;//y=w*x+b，初始w double b = 0;//y=w*x+b，初始b double true_w = 10.0;//真实w double true_b = 10.0;//真实b double alpha = 0.3;//步长 int samples = 1000;//样本数 double* x = new double[s
神经网络好难理解（一）：奇奇怪怪的损失函数Loss，函数本身是否始终一致
qq_44211389的博客
03-20 1260
奇奇怪怪的损失函数Loss 前言 本篇博客仅涉及直觉理解，不包括严谨的数学运算。默认读者已经很熟系神经网络的基本结构和反向传播过程，这里仅仅对损失函数的一小点知识做出个人理解，说错了请大哥们指正。 这里博主是看到了如下b站up主的视频链接有感而发的： https://www.bilibili.com/video/BV1bx411M7Zx?t=211 本篇小博客内容：loss函数本身在训练过程中是否不变 1.loss函数数学角度的输入输出关系： 从数学角度来看，神经网络本质上是一个函数，叫它f(x);Los
最速下降法 python_Python机器学习库Sklearn系列教程（16）-SGD梯度下降法
weixin_39763683的博客
11-27 817
随机梯度下降(SGD) 是一种简单但又非常高效的方法，主要用于凸损失函数下线性分类器的判别式学习，例如(线性) 支持向量机 和 Logistic 回归 。Stochastic Gradient Descent (随机梯度下降法)的优势:高效。易于实现 (有大量优化代码的机会)。Stochastic Gradient Descent (随机梯度下降法)的劣势:SGD 需要一些超参数，例如 regul...
神经网络中的损失函数
wmsbeijing的专栏
12-10 1万+
cnn进行前向传播阶段，依次调用每个Layer的Forward函数，得到逐层的输出，最后一层与目标函数比较得到损失函数，计算误差更新值，通过反向传播逐层到达第一层，所有权值在反向传播结束时一起更新。 loss layer 是CNN的终点，接受两个Blob作为输入，其中一个是CNN的预测值，另一个是真实标签。损失层则将这两个输入进行一系列运算，得到当前网络的损失函数（Loss Function
adopt mini-batch stochastic gradient descent
最新发布
09-27
小批量随机梯度下降（Mini - Batch Stochastic Gradient Descent，简称 Mini - Batch SGD）是一种结合了批量梯度下降（Batch Gradient Descent）和随机梯度下降（Stochastic Gradient Descent）优点的优化算法。以下是采用小批量随机梯度下降的一般步骤和代码示例： ### 步骤 1. **数据准备**：将数据集划分为多个小批量（Mini - Batch），每个小批量包含固定数量的样本。 2. **初始化参数**：为模型的参数（如权重和偏置）随机初始化初始值。 3. **迭代更新**：在每个迭代中，选择一个小批量的数据，计算该小批量数据上的梯度，然后使用梯度更新模型的参数。 4. **重复步骤3**：直到满足停止条件，如达到最大迭代次数或损失函数收敛。 ### 代码示例 以下是使用Python和PyTorch库实现小批量随机梯度下降的示例代码： ```python import torch import torch.nn as nn import torch.optim as optim # 定义一个简单的线性模型 class SimpleModel(nn.Module): def __init__(self): super(SimpleModel, self).__init__() self.linear = nn.Linear(10, 1) # 输入维度为10，输出维度为1 def forward(self, x): return self.linear(x) # 生成一些示例数据 num_samples = 1000 input_dim = 10 x = torch.randn(num_samples, input_dim) y = torch.randn(num_samples, 1) # 初始化模型 model = SimpleModel() # 定义损失函数和优化器 criterion = nn.MSELoss() optimizer = optim.SGD(model.parameters(), lr=0.01) # 定义小批量大小 batch_size = 32 num_batches = num_samples // batch_size # 训练模型 num_epochs = 10 for epoch in range(num_epochs): for i in range(num_batches): # 获取当前小批量的数据 start_idx = i * batch_size end_idx = start_idx + batch_size batch_x = x[start_idx:end_idx] batch_y = y[start_idx:end_idx] # 前向传播 outputs = model(batch_x) loss = criterion(outputs, batch_y) # 反向传播和优化 optimizer.zero_grad() loss.backward() optimizer.step() print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}') ``` ### 相关问题
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值