【数据结构】二叉树

二叉树概念及结构

• 二叉树每个结点最多有两颗子树
• 二叉树的子树有左右之分，即二叉树是有序树
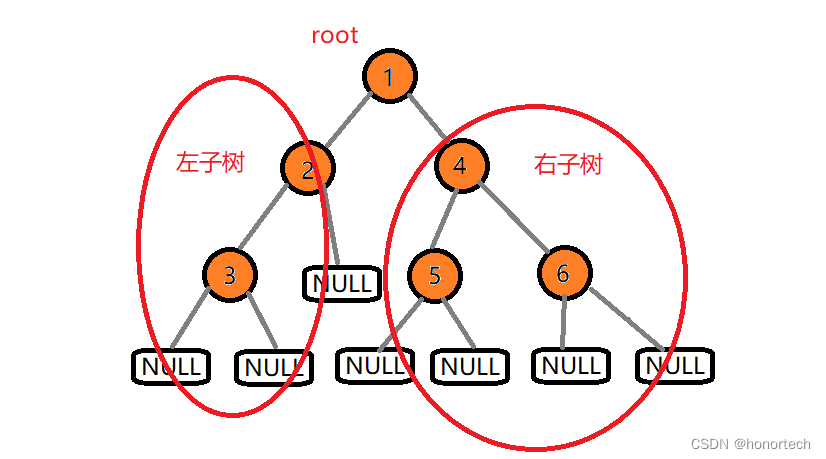
• 二叉树由根节点和左右子树构成(子树又可看成一个二叉树，由此可分治)

 
特殊的二叉树：

• 满二叉树：每一层结点数都为最大，若层数为k，则结点数为 2^k - 1
• 完全二叉树：一个h层二叉树，前h-1层为满，最后一层不满且最后一层的结点从左至右连续
• 

 

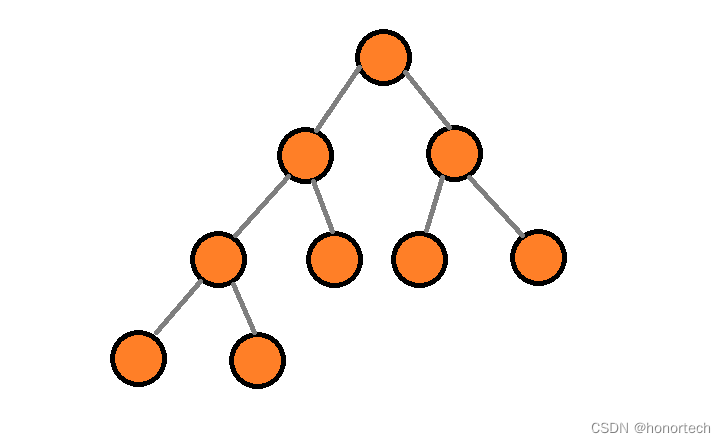
性质：

• 深度为h的二叉树最多有2^h-1个结点
• 第 i 层最多有 2^(i-1) 个结点
• 度为 0 的结点数为 n0，度为 2 的结点数为 n2，则 n0 = n2 + 1 (对于所有二叉树成立)
• N 个结点的满二叉树的深度 h = log2N + 1
• n 个结点的完全二叉树，按照堆实现顺序，将所有结点从 0 开始编号， 则对于序号为 i 的结点有：
  • 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
  • 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
  • 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子
     

性质列题：

解析：完全二叉树中，有n0 = n2 + 1
再根据题设条件，得n0 + n1 + n2 = 2n
则可得：2n0 + n1 - 1 = 2n
完全二叉树中，n1只能为0或1，由于2n为偶数，故n1 = 1
因此，n0 = n
 

二叉树链式结构实现

链式二叉树结构定义

typedef struct BTNode
{
	char data;
	struct BTNode* left;
	struct BTNode* right;
}BTNode;

二叉树是由根结点和左右子树构成的，即是递归式的，故后续基本操作基本都为递归操作(对左右子树分治)

 

二叉树的遍历

遍历方式：前序、中序、后序、层序
 
深度优先遍历：

• 前序遍历：先访问根结点，在分别遍历左右子树
• 中序遍历：先遍历左子树，再访问根结点，后遍历右子树
• 后序遍历：先遍历左子树，再遍历右子树，后访问根结点
• 

 

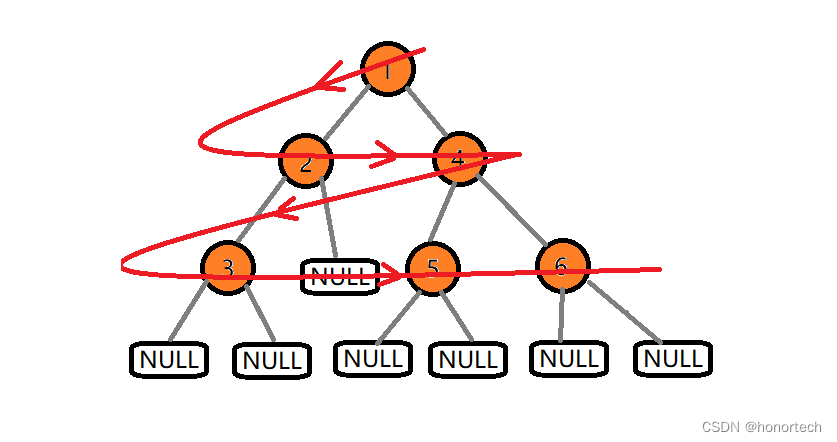
广度优先遍历：

• 层序遍历：自上而下、从左至右逐层访问树的结点的过程