Leetcode 84、柱状图中的最大矩形

Leetcode 84、柱状图中的最大矩形

方法一、动态规划

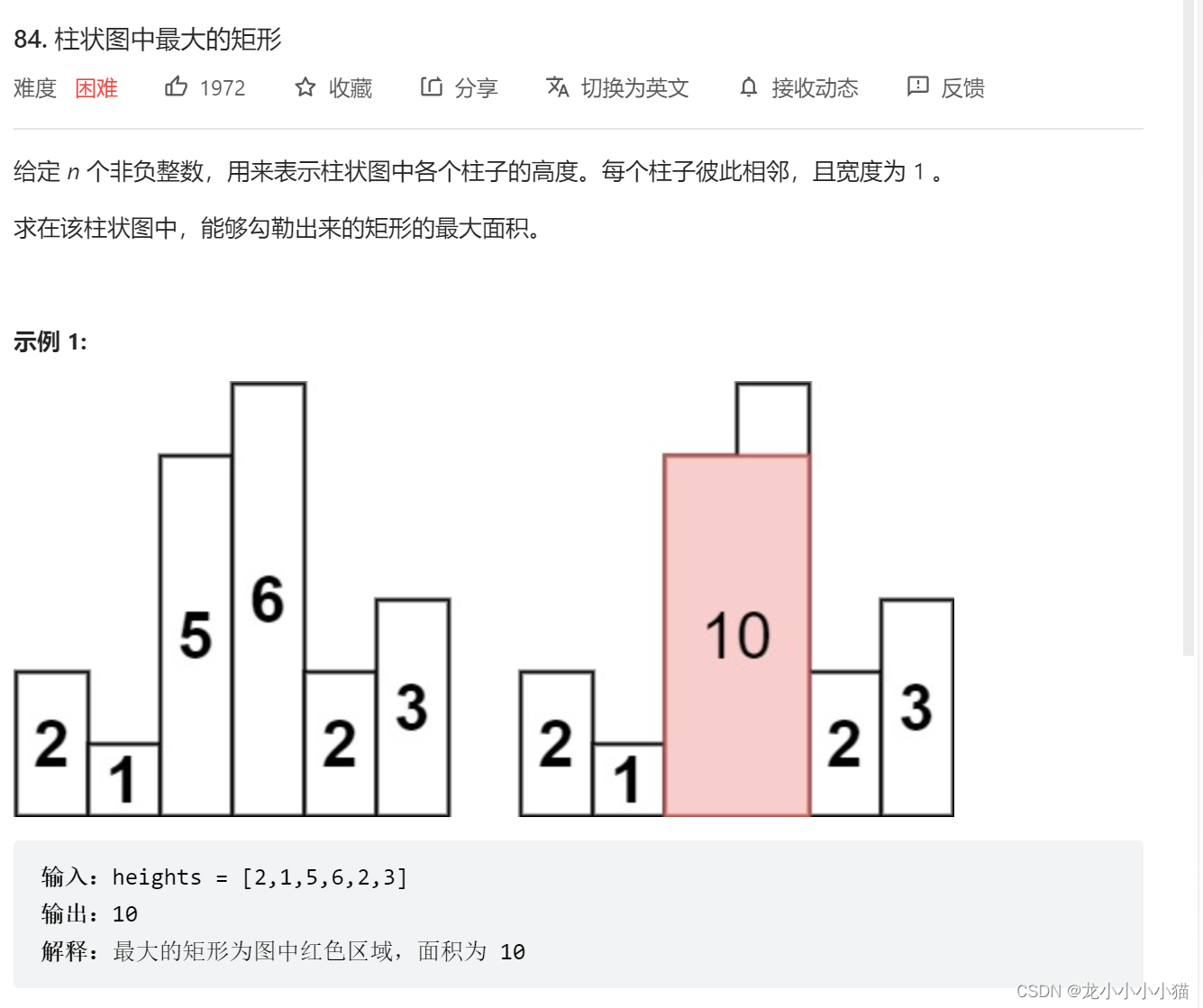
当前题目要求的是可以组成的矩形的最大面积，当前位置可以形成的矩形的最大面积，
取决于左右两边小于当前高度的位置，找到左右两边小于当前高度的下标，就可以确定
面积的宽度，就是左右两边下标中间为长度，也就是矩形的宽度，高度就是当前位置的值

     /**
     * 方法一、动态规划
     * 使用left和right数组分别存储当前位置左边，第一个小于当前高度的下标；和当前位置右边，第一个小于当前高度的下标，
     * 这样在最后计算的时候，高度就是当前的高度，宽度就是两边小于当前高度的下标中间的长度，right[i] - left[i] - 1；
     *
     * 首先两个双层循环给left和right赋值；
     * 单层循环找到最大值，返回result。
     * @param heights
     */
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        int[] left = new int[len];
        int[] right = new int[len];
        
        left[0] = -1;
        for(int i = 1; i < len; i++) {
            int l = i - 1; // 因为向左找，所以l = i - 1.
            while(l >= 0 && heights[l] >= heights[i]) {
                l = left[l]; // 如果l大于等于i，则去找小于l的下标，加快查找速度，如果一直l--，会超出时间限制。
            }
            left[i] = l;
        }

        right[len - 1] = len;
        for(int i = len - 2; i >= 0; i--) {
            int r = i + 1; // 因为向右找，所以r = i + 1.
            while(r < len && heights[r] >= heights[i]) {
                r = right[r]; // 如果r位置大于等于i位置，则去找小于r位置的下标，加快查找速度。
            }
            right[i] = r;
        }

        int result = 0;
        for(int i = 0; i < len; i++) {
            // 因为left和right存储的是小于当前位置高度的第一个下标，所以高度是当前位置，宽度是两边下标中间的宽度；
            // 因为对于两个下标中间的位置，heights[i]是最高的。
            int sum = heights[i] * (right[i] - left[i] - 1);
            result = Math.max(result, sum);
        }

        return result;
    }

方法二、双指针

和动态规划的思路一样，只不过是在遍历的时候直接更新result的值。

/**
        3、双指针
        超出时间限制
        时间复杂度：O(n*n)
     */
    public int largestRectangleArea(int[] heights) {
        int result = 0;
        for(int i = 0; i < heights.length; i++) {
            int left = i, right = i;
            for(left = i - 1; left >= 0; left--) {
                if(heights[left] < heights[i]) {
                    break;
                }
            }

            for(right = i + 1; right < heights.length; right++) {
                if(heights[right] < heights[i]) {
                    break;
                }
            }

            int sum = heights[i] * (right - left - 1);
            result = Math.max(result, sum);
        }
        return result;
    }

方法三：单调栈

对于单调栈，最重要的是确定当前栈是递增的还是递减的，然后在遇到符合要求
的高度的时候，使用while循环累加result，最后返回result。

/**
        单调栈
     */
    public int largestRectangleArea(int[] heights) {
        Stack<Integer> st = new Stack<Integer>();
        
        // 数组扩容，在头和尾各加入一个元素
        int [] newHeights = new int[heights.length + 2];
        newHeights[0] = 0;
        newHeights[newHeights.length - 1] = 0;
        for (int index = 0; index < heights.length; index++){
            newHeights[index + 1] = heights[index];
        }

        heights = newHeights;
        
        st.push(0);
        int result = 0;
        // 第一个元素已经入栈，从下标1开始
        for (int i = 1; i < heights.length; i++) {
            // 注意heights[i] 是和heights[st.top()] 比较 ，st.top()是下标
            if (heights[i] > heights[st.peek()]) {
                st.push(i);
            } else if (heights[i] == heights[st.peek()]) {
                st.pop(); // 这个可以加，可以不加，效果一样，思路不同
                st.push(i);
            } else {
                while (heights[i] < heights[st.peek()]) { // 注意是while
                    int mid = st.peek();
                    st.pop();
                    int left = st.peek();
                    int right = i;
                    int w = right - left - 1;
                    int h = heights[mid];
                    result = Math.max(result, w * h);
                }
                st.push(i);
            }
        }
        return result;
    }