吃透链表进阶OJ：从 “怕踩坑” 到 “能讲透”-优快云博客

typedef struct ListNode ListNode;
int kthToLast(struct ListNode* head, int k)
{
    ListNode *fast=head,*slow=head;
    while(k--)
    {
        fast=fast->next;
    }
    while(fast)
    {
        fast=fast->next;
        slow=slow->next;
    }

    return slow->val;  
}

二、相交链表

Leetcode链接:相交链表

题目描述：

2.1题目思路分析

思路：

         ①判断两个链表是否相交：链表的尾节点作为依据，如果两个链表相交则两个链表的尾节点必然相同，反之两个链表的尾节点不同，两个链表不可能相交。



②（查找方式一）寻找两个链表的公共节点：先找到较长的链表，通过暴力查找的方式，遍历长链表的每一个节点时，都在短链表中查找一遍，判断是否两个节点的地址相同。这种查找方式时间复杂度为O(N^2)



③（查找方式二）寻找两个链表的公共节点：先让较长的链表先查找到与短链表一样的长度的节点位置，然后两者一起查找，判断两个节点的地址是否相同。这种查找方式时间复杂度就为O(N)。



温馨提示：这里判断公共节点，断然不可以用两个节点的值是否相同来作为依据，而应该通过两个节点的地址是否相同来作为依据。

2.2代码实现

查找方式一：时间复杂度为O（N^2）

typedef struct ListNode ListNode; 
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
    //如果两个链表相交则链表的尾节点必然相同
    ListNode * pcura=headA;
    ListNode * pcurb=headB;

    int lena=1,lenb=1;
    while(pcura->next)
    {
        pcura=pcura->next;
        lena++;
    }

    while(pcurb->next)
    {
        pcurb=pcurb->next;
        lenb++;
    }
    if(pcura!=pcurb) return NULL;

    //利用假设法判断a,b的链表长度
    ListNode * longList=headA,* shortList=headB;
    if(lenb>lena)
    {
        longList=headB;
        shortList=headA;
    }
    ListNode *p1=longList,*p2=shortList;

    while(p1)
    {
        while(p2)
        {
            if(p1==p2) return p2; 
            p2=p2->next;
        }
        p2=shortList;
        p1=p1->next;
    }
    return NULL;
}

查找方式二：时间复杂度为O（N）

typedef struct ListNode ListNode; 
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB)
{
    //如果两个链表相交则链表的尾节点必然相同
    ListNode * pcura=headA;
    ListNode * pcurb=headB;

    int lena=1,lenb=1;
    while(pcura->next)
    {
        pcura=pcura->next;
        lena++;
    }

    while(pcurb->next)
    {
        pcurb=pcurb->next;
        lenb++;
    }
    if(pcura!=pcurb) return NULL;

    //利用假设法判断a,b的链表长度
    int gap=abs(lenb-lena);
    ListNode * longList=headA,* shortList=headB;
    if(lenb>lena)
    {
        longList=headB;
        shortList=headA;
    }
    while(gap--)
    {
        longList=longList->next;
    }
    while(longList != shortList)
    {
      longList=longList->next;
      shortList=shortList->next;
    }
    return longList;
}

三、回文链表

Leetcode链接:回文链表

题目描述

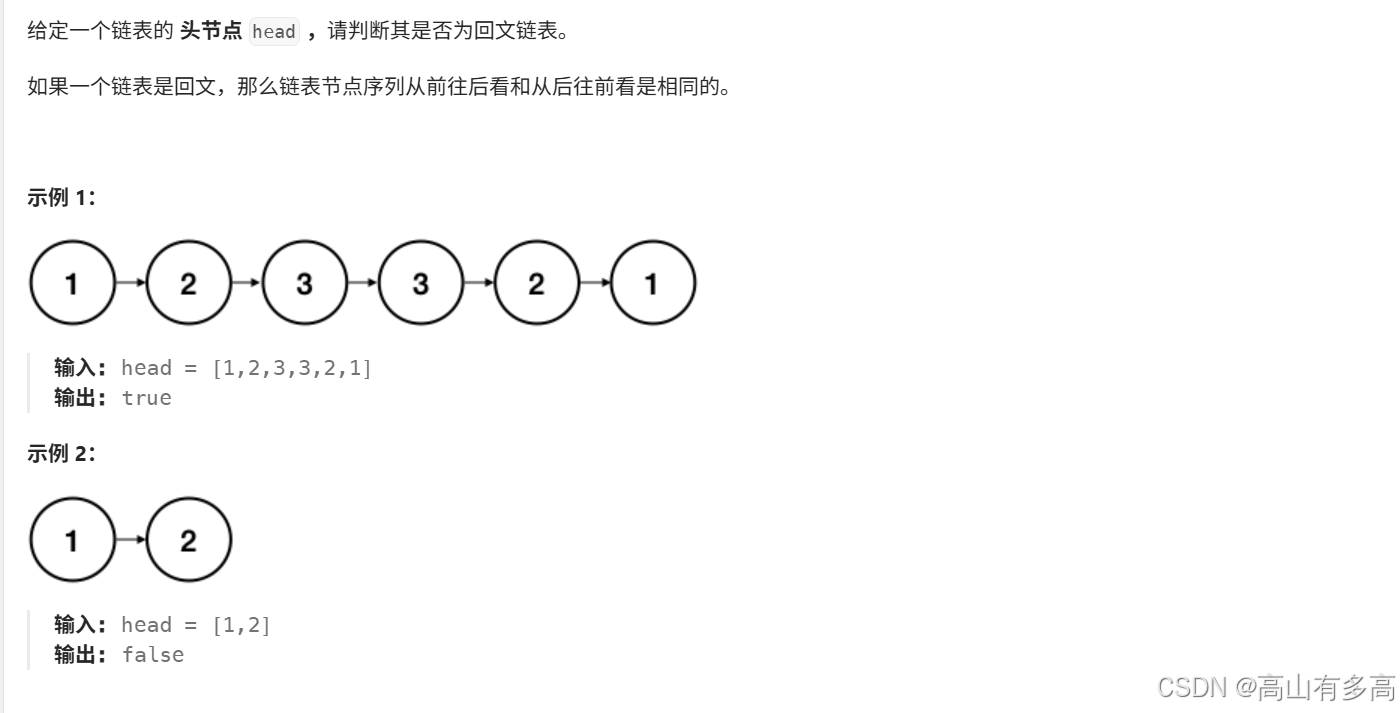
3.1题目思路分析

思路：



①对于在一个数组中，判断回文序列我们已经很熟悉了，通过定义双向指针，一个指向头部，另一个指向尾部，通过两个指针不断逼近的方式进行判断数值是否相同，来断定是否为回文序列。



②对于一个单向不循环链表而言，因为其只能从前往后进行遍历，而不能从后往前进行遍历，所以双向指针的方式失效了，但是也可以通过将单向链表转换为双向链表进行判断，但是这样需要开辟额外的空间，空间复杂度为O(N)。



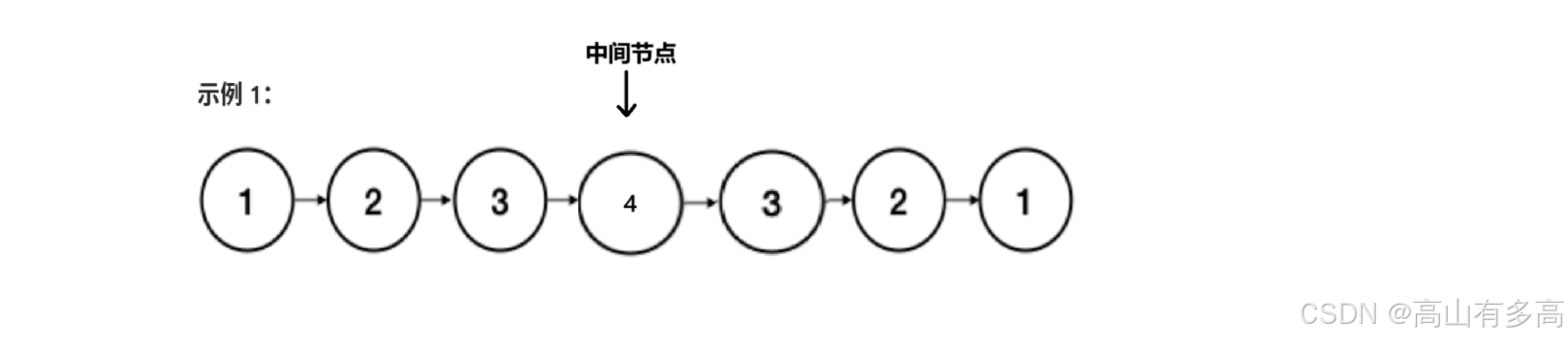
③实际上这道题可以通过查找中间节点+反转链表这两个组合拳实现空间复杂度为O(1), 通过查找到中间节点的位置，将中间节点以后的节点进行逆置，将原链表的头节点到中间节点这一部分作为链表1，将逆置后的链表作为链表2，通过分别遍历两个链表判断两个链表的值是否相同。

如下图所示：



1.原链表



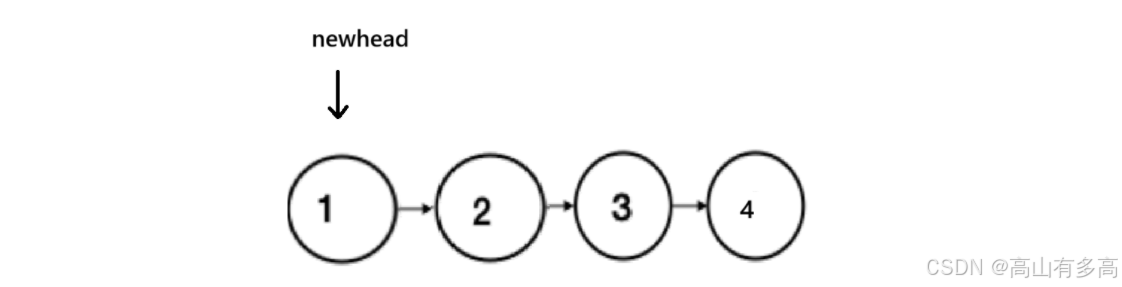
2. 链表1



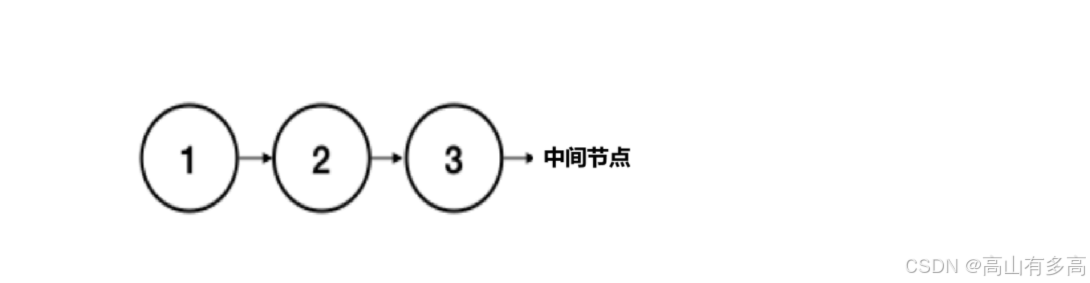
3.链表2

3.2代码实现

//查找链表的中间节点
ListNode * findMid(ListNode * head)
{
    ListNode *slow=head,*fast=head;
    while(fast && fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
    }
    return slow;
}

//反转链表
ListNode * reverseList(ListNode * head)
{
    ListNode * newhead=NULL;

    ListNode * pcur=head;
    
    while(pcur)
    {
        ListNode * tmp=pcur->next;
        pcur->next=newhead;
        newhead=pcur;
        pcur=tmp;        
    }

    return newhead;
}

bool isPalindrome(struct ListNode* head)
{
    ListNode* pmid=findMid(head);
    
    ListNode* newhead=reverseList(pmid);  
    
    ListNode* pcur=head;

    while(pcur!=pmid)
    {
        if(pcur->val!=newhead->val)
        {
            return false;
        }
        pcur=pcur->next;
        newhead=newhead->next;
    }
    return true;
}

四、拷贝复杂链表

Leetcode链接:拷贝复杂链表

题目描述：

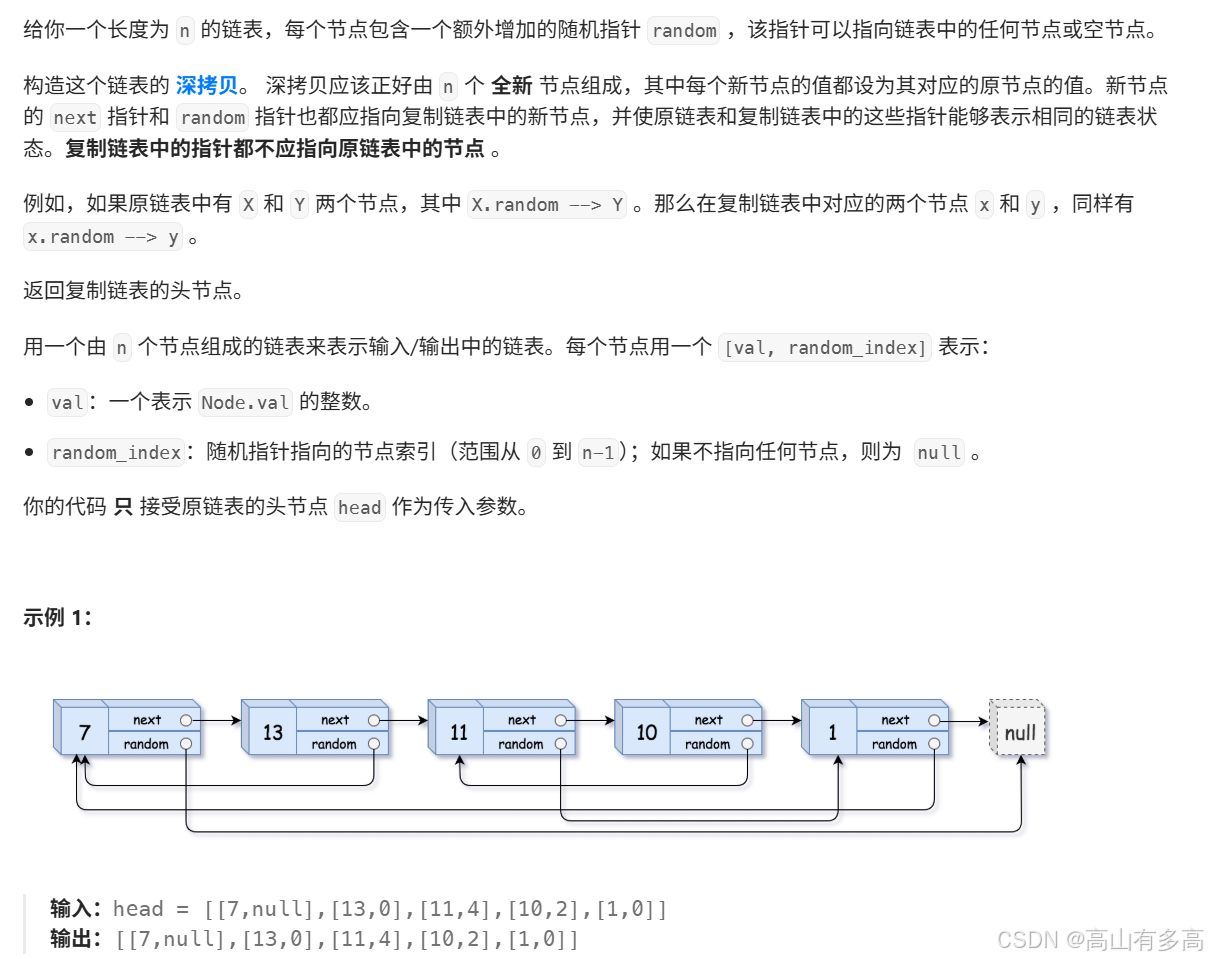
4.1 题目思路分析

思路：

①理解深拷贝这个概念，拷贝一个值和指针指向都与当前链表一模一样的链表，但是复制链表的指针都不能指向原链表。



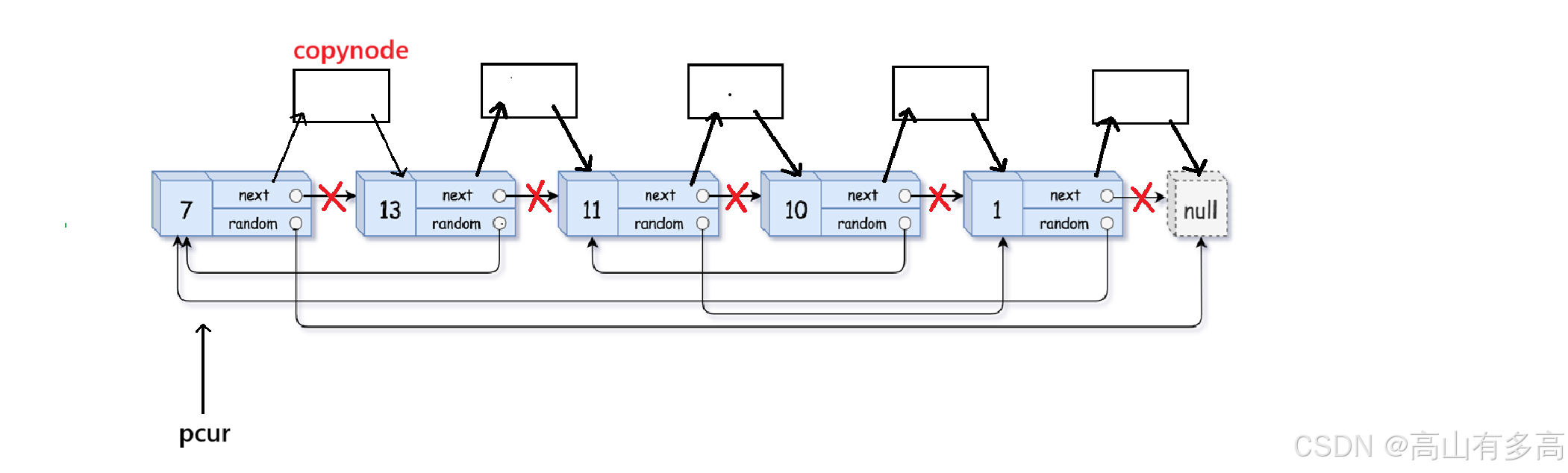
②我们可以将该链表中每一个节点拆分为两个相连的节点，例如对于链表 A→B→C，我们可以将其拆分为 A→A′→B→B′→C→C′，也就是说在原链表中的每一个节点后插入一个拷贝节点，如下图所示：





对于任意一个原节点 S，其拷贝节点 S′ 即为其后继节点，我们可以找到每一个拷贝节点S′的任意节点指针的指向，比如说第二个节点任意指针的指向是第一个节点，所以第二个拷贝节点任意指针的指向是第一个节点的后继节点。



温馨提示：需要注意原节点的随机指针可能为空，我们需要特别判断这种情况。



③通过将每个拷贝节点进行剪下来，在串联起来就是我们需要寻找的拷贝链表

4.2代码实现

typedef struct Node Node;
struct Node* copyRandomList(struct Node* head)
{
    if(head==NULL) return NULL;
    Node* pcur=head;

    //插入节点
    //在每个节点后面添加一个节点作为复制节点
    while(pcur)
    {
        Node *newnode=(Node*)malloc(sizeof(Node));
        Node * tmp=pcur->next;
        pcur->next=newnode;
        newnode->val=pcur->val;
        newnode->next=tmp;
        pcur=newnode->next;
    }

    //核心环节
    //修改每个复制节点的random节点
    pcur=head;
     
    while(pcur)
    {
        Node * copynode=pcur->next;
        //判断random节点是否为空
        if(pcur->random==NULL)
            copynode->random=NULL;
        else
            copynode->random=pcur->random->next;
        pcur=copynode->next;
    }

    //尾插节点
    //拆除复制节点
    pcur=head;
    Node * dummy=(Node*)malloc(sizeof(Node));
    Node * ptail=dummy;
    
    while(pcur)
    {
        Node * copynode=pcur->next;
        ptail->next=copynode;
        ptail=copynode;
        pcur->next=copynode->next;
        pcur=copynode->next; 
    }
    Node * ret=dummy->next;
    free(dummy);
    dummy=NULL;
    return ret;
}

五、环形链表Ⅰ(重点)

Leetcode链接:环形链表Ⅰ

题目描述：

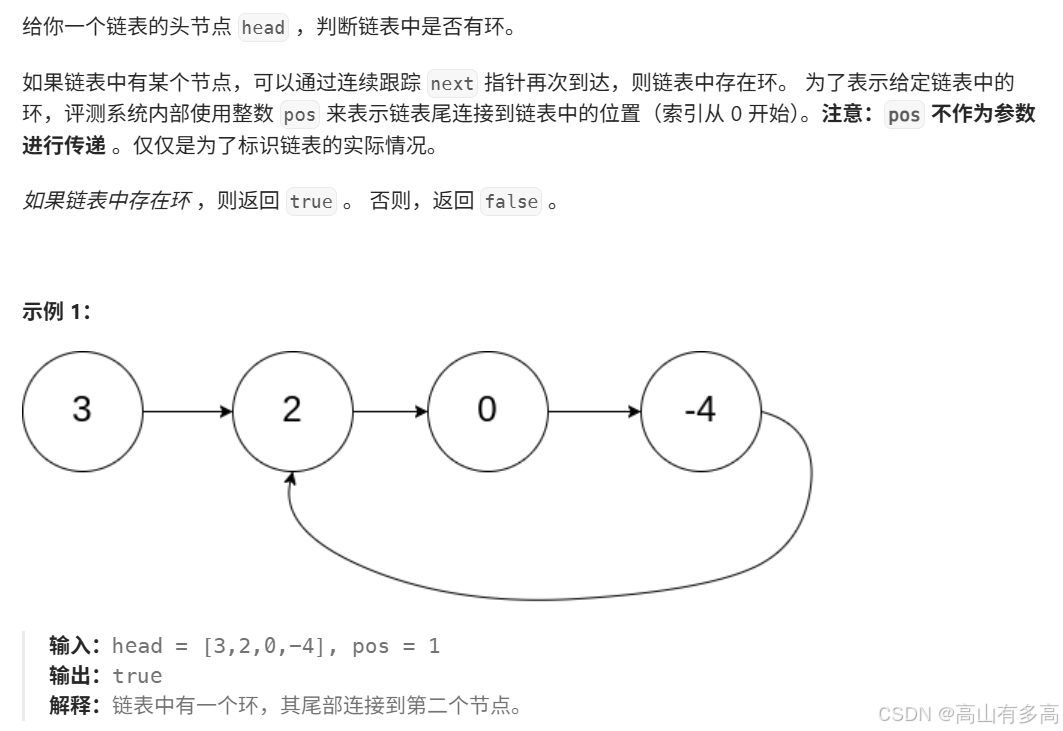
5.1 题目思路分析

思路：



①利用快满指针的方式，快指针走二步，满指针走一步，当满指针进入环内，相当于快指针追击满指针，两者一定会在环内相遇。



②证明如下：

        我们可以这样理解：假设链表存在环，当 slow 进入环时，设此时 slow 和 fast 在环内的距离为 N。因为 fast 每次走 2 步，slow 每次走 1 步，那么每经过 1 次移动，fast 相对于 slow 就多走了1步，这就使得它们在环内的距离缩小 1。



        所以距离从 N 开始，依次变为N-1→N-2→N-3→……→3→2→1→0 不断缩小，最终一定会缩小到 0，此时 slow 和 fast 就相遇了。



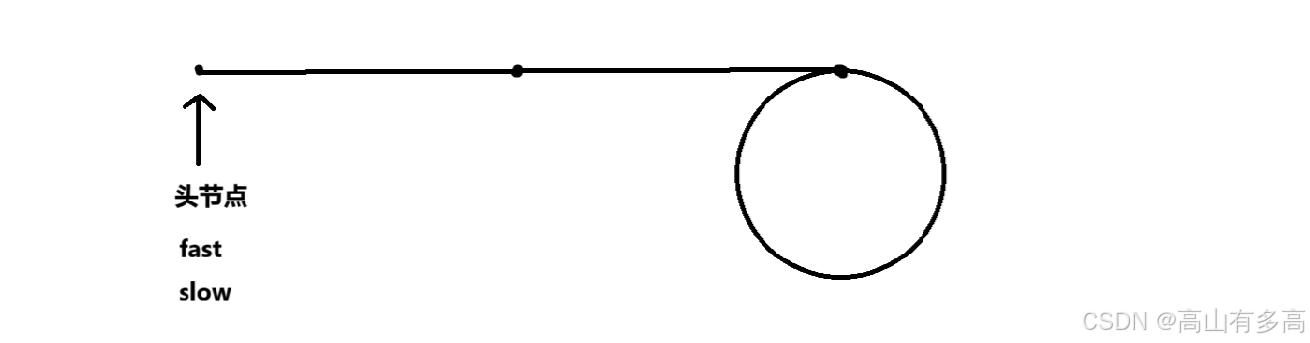
③如图所示：



初始状态：slow和fast同时指向头节点



临界状态：slow刚进入环内



最终状态：slow和fast相遇

5.2代码实现

typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head)
{
   ListNode * fast=head, * slow=head;
   //如果fast或则fast->next已经是NULL说明此时单链表没有带环 
    while(fast && fast->next)
    { 
        //慢指针走一步，快指针走两步
        //两者一定会在环内相遇  
        slow=slow->next;  
        fast=fast->next->next;   
        if(fast==slow)
        {
            return true;
        }   
    }
    return false;
}

5.3深入研究

思考：如果慢指针走一步，快指针一次走三步、四步、......、N步，是否快慢指针还会在环内相遇呢？

接下来：以慢指针走一步，快指针走三步为例进行深入讨论

如下图所示：



初始状态：slow和fast同时指向头节点



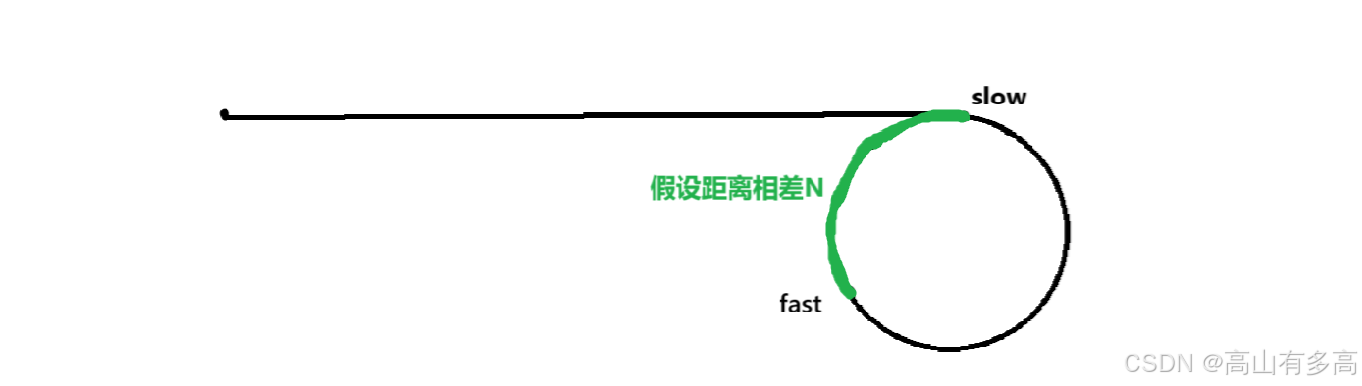
临界状态：slow刚进入环内

假设 slow刚进入环内时，两者距离相差为N，由于slow指针一次走一步，fast指针一次走三步，所以每走一次两者的距离差距缩小2。



若N为偶数时，两个指针之间相差的距离：N→N-2→N-4→N-6→......→4→2→0

所以此时slow和fast一定会在环内相遇。



若N为奇数时，两个指针之间的相差的距离：N→N-2→N-4→N-6→......→3→1→-1



如何理解距离为-1呢，我们假设整个环的长度大小为C？



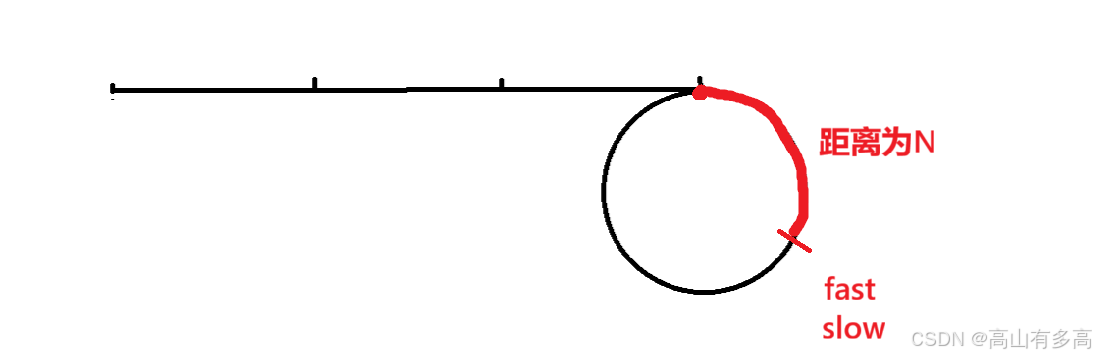
①我们先看一下距离为1的情况，如图所示：





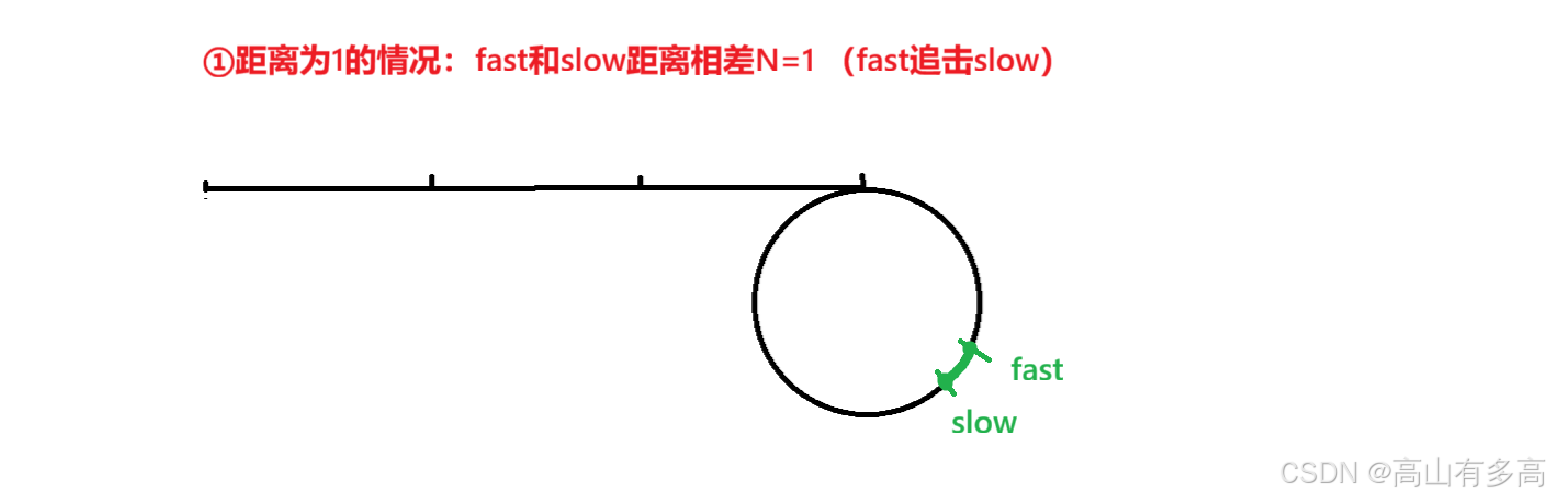
②我们再看一下距离为-1的情况，如图所示：

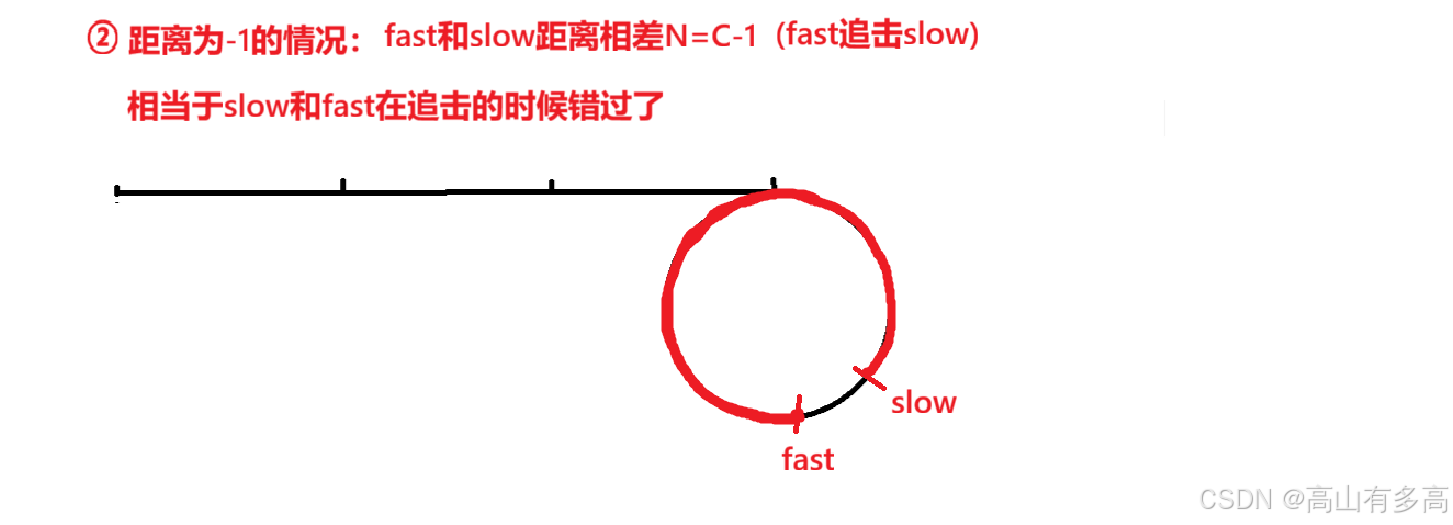
总结一下：



若初始距离 N 是偶数，第一轮就能追上。

若初始距离 N 是奇数，第一轮追不上；此时再看环的长度 C：
若环长 C 是奇数（此时 N = C - 1 会变成偶数），第二轮能追上。
若环长 C 是偶数（此时 N = C - 1 仍为奇数），永远追不上，会进入 “追不上的死循环”。

那么C与N的关系究竟是如何的呢？以slow刚进入环时，这个临界条件进行讨论。



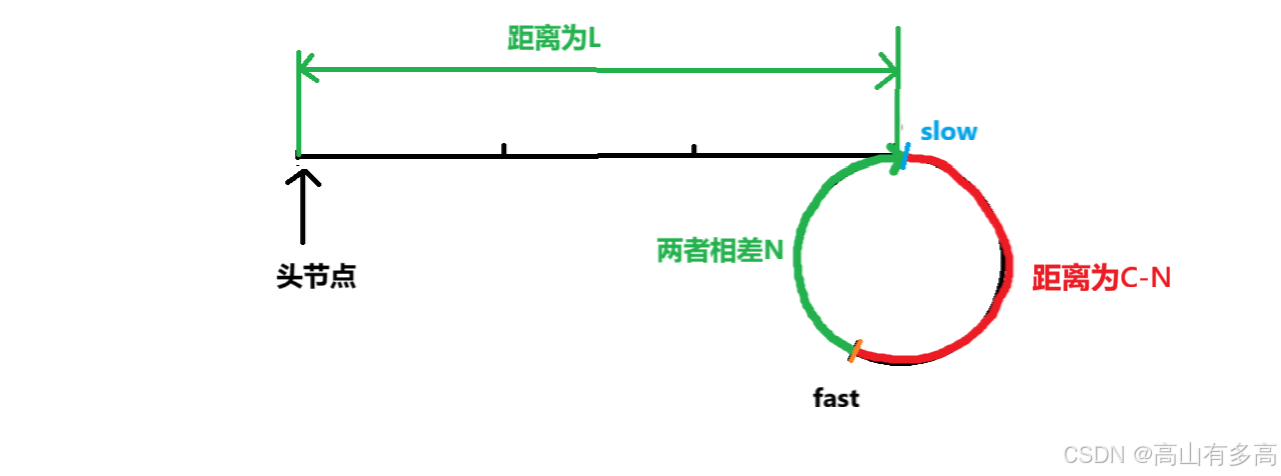
如图所示当slow指针刚进入环内：



先通过路程关系列等式：慢指针走了 L，快指针走了 3L 。



快指针的路程也可表示为 “慢指针到环入口的距离 L” + “环内已走的 x 圈（x*C）” + “环内剩余距离(C - N)”



则有等式：3 L = L + x * C + C - N



化简得：2 L = ( x + 1 ) * C - N



再分析奇偶性：左边 2L 是偶数；



若假设 “N 为奇数、C 为偶数”，

右边会是 “ 偶数（ ( x + 1 ) * C ） - 奇数（N）= 奇数 ”，与左边 “偶数” 矛盾，所以这种情况不可能出现。



故而当N为奇数时，C只能为奇数。

综上所述：(fast指针一次走三步，slow指针一次走一步的情况，其余情况可以类比推理)

当N为奇数时，C只能为偶数，此时fast指针第一圈追不上，在第二圈追上。

当N为偶数时，C不管奇偶性，此时fast指针在第一圈都能够追上。

六、环形链表Ⅱ(重点)

Leetcode链接:环形链表Ⅱ

题目描述：

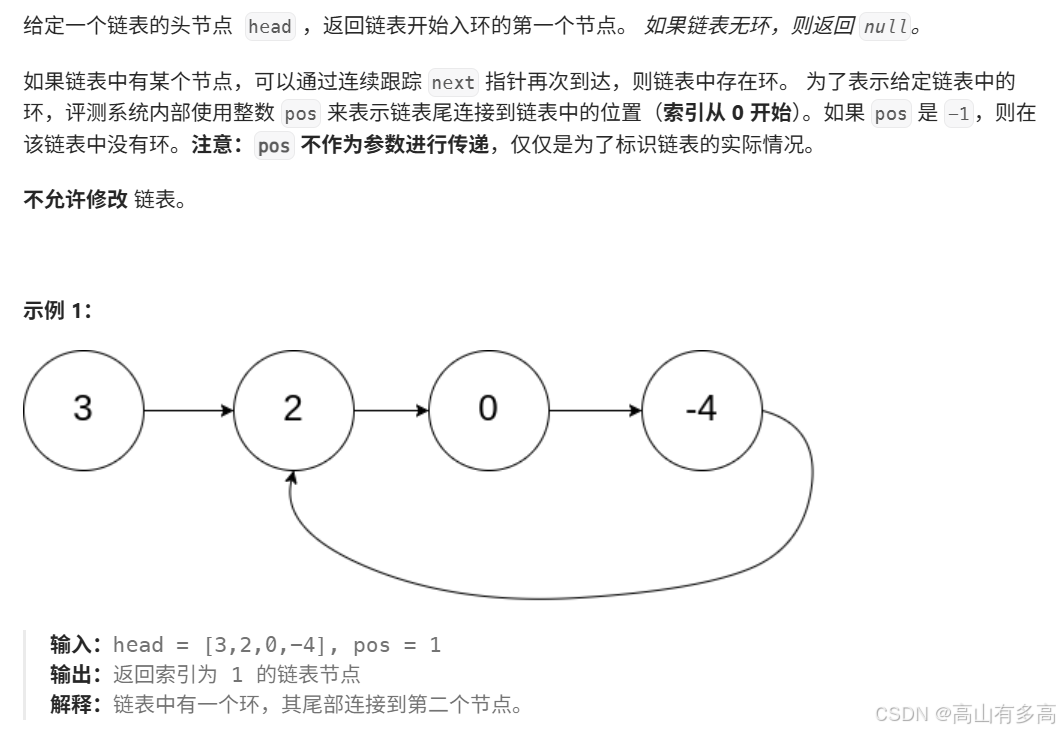
6.1题目思路分析

思路：



①通过对上一题的思路分析，我们可以知道入环的第一个节点，就是我们的临界情况，即slow指针刚好进入环内。



②我们可以通过快慢指针的方式，让快指针：fast一次走两步，让慢指针：slow一次走一步，slow指针刚进入环的时候，就是我们寻求的环上第一个节点。



③ 我们如何知道slow指针刚进入环内呢，接下来我们通过数学进行分析，如何判断slow进入环。

如图所示：slow刚进环的情况

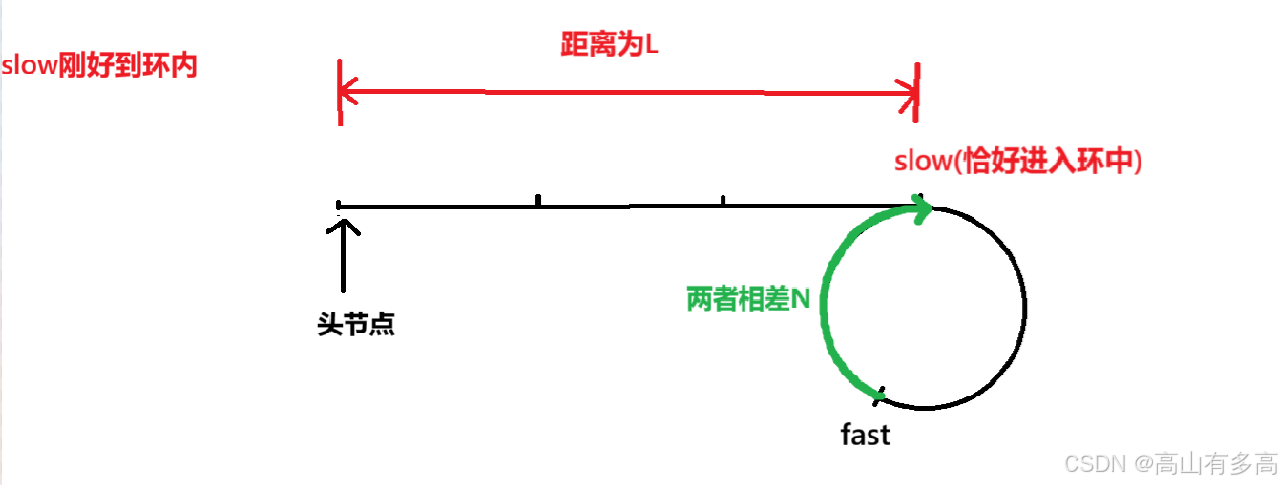
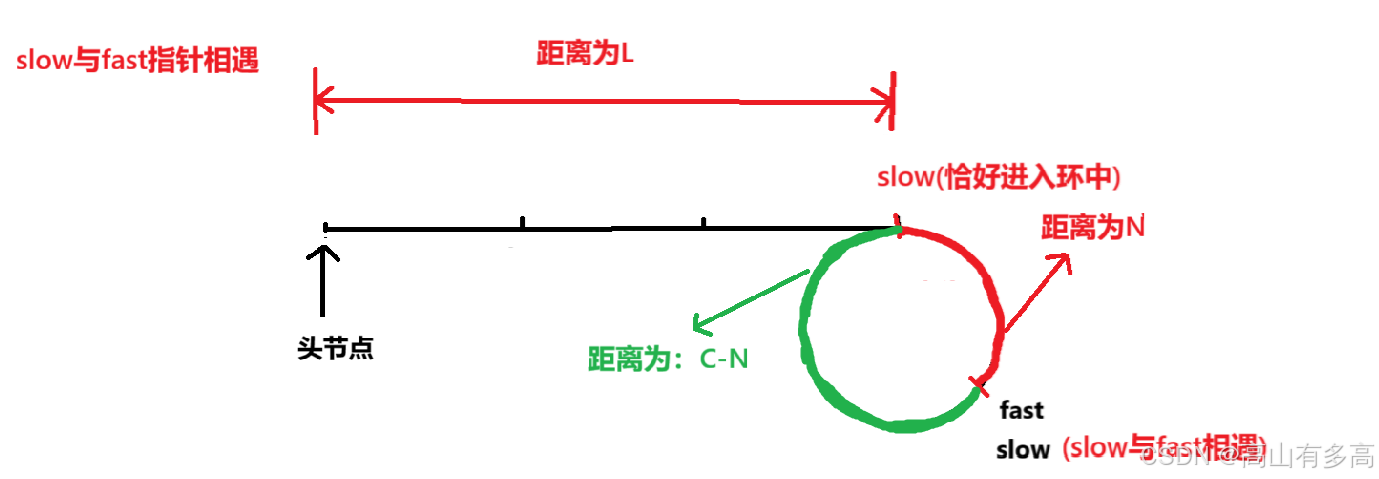
如图所示：slow和fast指针相遇的情况

数学推导：（快指针fast一次走两步，慢指针slow一次走一步）



情景分析：



把链表的 “环” 想象成 “环形跑道”，fast 先跑进 “跑道（环）”，slow 后跑进 “跑道”。当 slow 刚进环时，和 fast 在环内有个距离差 N；由于 fast 速度是 slow 的 2 倍，相当于每走一次，fast 相对于 slow 的距离就缩短 1。



因为 fast 一开始就领先在环里，所以在 slow 走完环的第一圈之前，fast 肯定能追上 slow（slow 走不完一整圈就会被追上）。



①设置未知数



设 “链表表头到环入口的距离” 为 L，“slow 刚进环时与 fast 的环内距离差” 为 N，“环的长度” 为 C。



②相遇时：



slow 走的路程是 L + N（从表头到环入口的 L，加环内走的 N）。



fast 走的路程是 (L + x*C + N)（从表头到环入口的 L，加环内绕了 x 圈的x*C)，再加与 slow 的距离 N，且(x>=1)，因为 fast 先进环）。



③建立等式：



L + x * C + N = 2 * ( L + N )



④化简得：



L = x * C - N = (x-1)*C + C-N



⑤得出结论：



从链表的头节点开始走与从快慢指针相遇的位置走，两者距离环入口的距离是一致的，故而可以让一指针从头开始走，另一个指针从快慢指针相遇的位置开始走，两者相遇的位置就是环入口的位置。

6.2代码实现

typedef struct ListNode ListNode; 
struct ListNode *detectCycle(struct ListNode *head)
{
    ListNode * fast=head, * slow=head;
    ListNode * meet=NULL;
    //定义一个快指针，一个慢指针
    //快慢指针相遇,如果链表中无环meet=NULL
    while(fast && fast->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(slow==fast)
        {
            meet=slow;
            break;
        }
    }

    //定义一个指针从头节点开始走
    ListNode * start=head;

    //两个指针相遇的节点就为环入口节点，保证meet不为空指针
    while(start != meet && meet)
    {
        meet=meet->next;
        start=start->next;
    }

    return meet;
}

既然看到这里了，不妨点赞+收藏，感谢大家，若有问题请指正。