直击痛点链表经典算法

前言         

        通过了解单链表的结构与实现，接下来小编将带大家深入探讨单链表的常见操作及其应用场景。我们将通过以下单链表经典算法题来深入理解单链表的特性和应用，每个算法题都配有详细的解题思路、代码实现和复杂度分析，建议读者先尝试独立解决，再参考给出的解决方案。

        

目录栏：

前言         

一、移除链表元素

二、反转链表

三、合并两个有序链表

四、链表的中间节点

五、分割链表

六、环形链表的约瑟夫问题

---

        

一、移除链表元素

Leetcode链接：移除链表元素

题目描述：

​

        

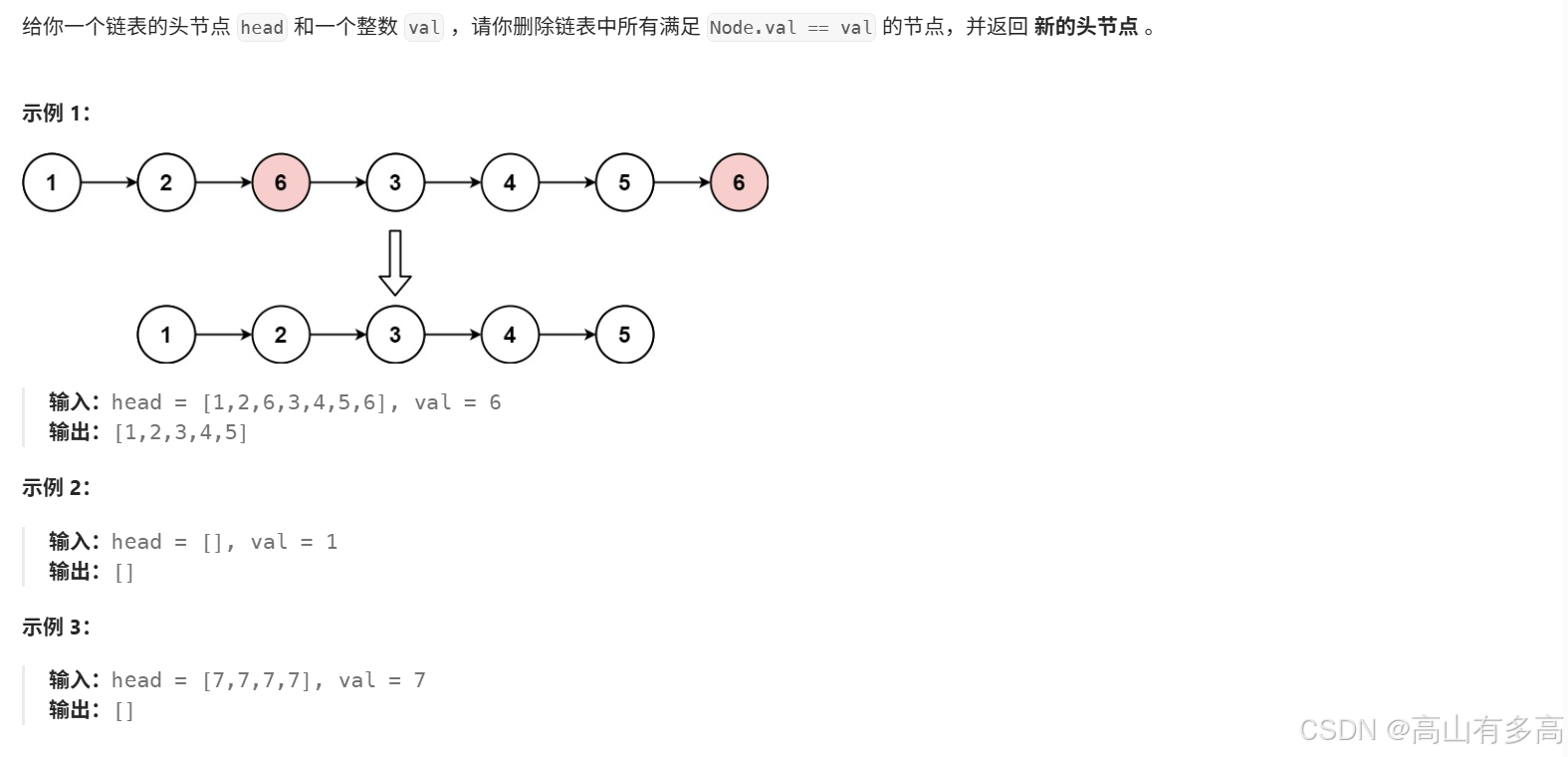
1.1题目思路剖析

思路一：在原链表中进行更改

        

①定义一个pcur指针初始化为头节点，通过循环遍历单链表，寻找链表元素为val值。

                

②如果遇到当前节点 为val值进行删除，类似于单链表中指定位置删除。

        

③需要定义一个前驱指针进行保存pcur的下一个节点位置，以防删除当前节点找不到下一个节点。    

    

简而言之：

        

要想删除节点 node，必须在 node 的前一个节点执行删除操作。

        

例如链表 1→2→3，要想删除 2，必须在节点 1 处操作，也就是把节点 1 的 next 更新为节点 3

        

温馨提示：需要去提前判断头节点处的值是否为val，如果头节点处的值为val需要进行提前删除，否则后续逻辑将混乱。

---

思路二：创建一个新的链表

        

①申请一个新的链表，定义头节点为newHead，定义尾节点为ptail。

        

②定义一个pcur节点指针初始化为原链表的头节点，进行循环遍历，如果当前节点不是val值，进行尾插到新链表中。

        

这里我们称这个头节点为哨兵位，并将该节点的指针域置为空，我们并不关系其数据域的内容，因为我们只需要返回newHead->next。

        

如图所示

        

        

1.2代码实现

思路一：代码实现

struct ListNode* removeElements(struct ListNode* head, int val) {

    //链表为空时
    if(head==NULL)
    {
        return NULL;
    }

    //判断val为头节点
    while(head&&head->val==val)
    {
        struct ListNode *tmp=head;  
        head=head->next;
        free(tmp);
        tmp=NULL;
    }
    struct ListNode * pcur=head;  //当前节点
    struct ListNode * prev=head;  //前驱节点
    //链表不为空时,遍历整个链表
    while(pcur)
    {
        //判断当前节点元素是否与val值相同
        if(pcur->val==val)
        {
            //删除当前节点
            prev->next=pcur->next;
            free(pcur);
            pcur=prev->next;
        } 
        else
        {
         //更新前驱节点的位置
         prev=pcur;
         //指向下一个节点
         pcur=pcur->next;
        }  
        
    }
    return head;

}

温馨提示：这里尤其要注意如下代码

      

    while(head&&head->val==val)
    {
        struct ListNode *tmp=head;  
        head=head->next;
        free(tmp);
        tmp=NULL;
    }

因为我们定义了一个前驱节点prev指向头节点，定义一个pcur指向当前节点，所以链表的头节点没有前驱节点，其删除逻辑与中间节点不同。

        

如果不单独处理头节点，直接进入后面的循环（依赖prev指针），会因为prev初始值也是头节点而无法正确删除头部的目标节点。

        

思路二：代码实现

typedef struct ListNode ListNode; 
struct ListNode* removeElements(struct ListNode* head, int val)
{
    //创建新链表的方式
    //创建两个指针，一个为头节点指针，另一个为尾节点指针
    ListNode * newHead=(ListNode*)malloc(sizeof(ListNode));
    newHead->next=NULL;
    ListNode * pTail=newHead;
    
    //遍历原链表
    ListNode * pcur=head;
    while(pcur)
    {
        if(pcur->val!=val)
        {
            //进行尾插节点
            pTail->next=pcur;
            //更新尾节点
            pTail=pTail->next;
        }
        pcur=pcur->next;
    }
    if(pTail!=NULL)
    {
        pTail->next=NULL;
    }
    ListNode *ret=newHead->next;
    free(newHead);
    newHead=NULL;
    return ret;
}

温馨提示：

        

这里我们通过定义一个新的链表，对不是val值的节点进行尾插，最后对动态内存开辟的空间进行释放，返回哨兵位的下一个节点。

        

1.3优化与复盘

通过这道题我们可以得到两种思路：

        

①在原链表进行修改。

                

进行删除某个节点时，我们一般会定义两个指针变量，prev指针为前驱节点（用于保存pcur指针的下一个节点，防止因删除后不能正确查找到下一个节点的位置），pcur指针（指向当前节点，进行对当前节点释放）

        

②新创建一个链表，基于新链表进行处理。

        

二、反转链表

 Leetcode链接：反转链表

题目描述：

​

        

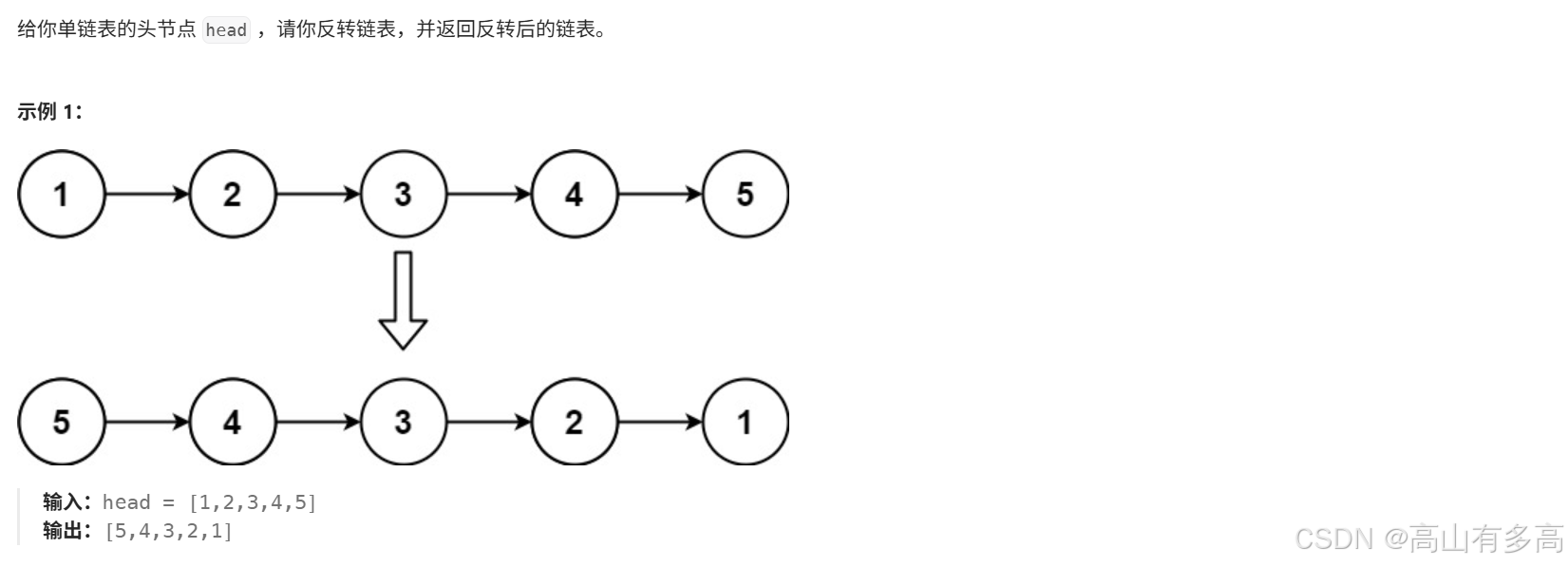
2.1题目思路剖析

思路一：头插法

        

开辟一个新链表，对新链表进行头插每个节点

                

思路二：迭代法

        

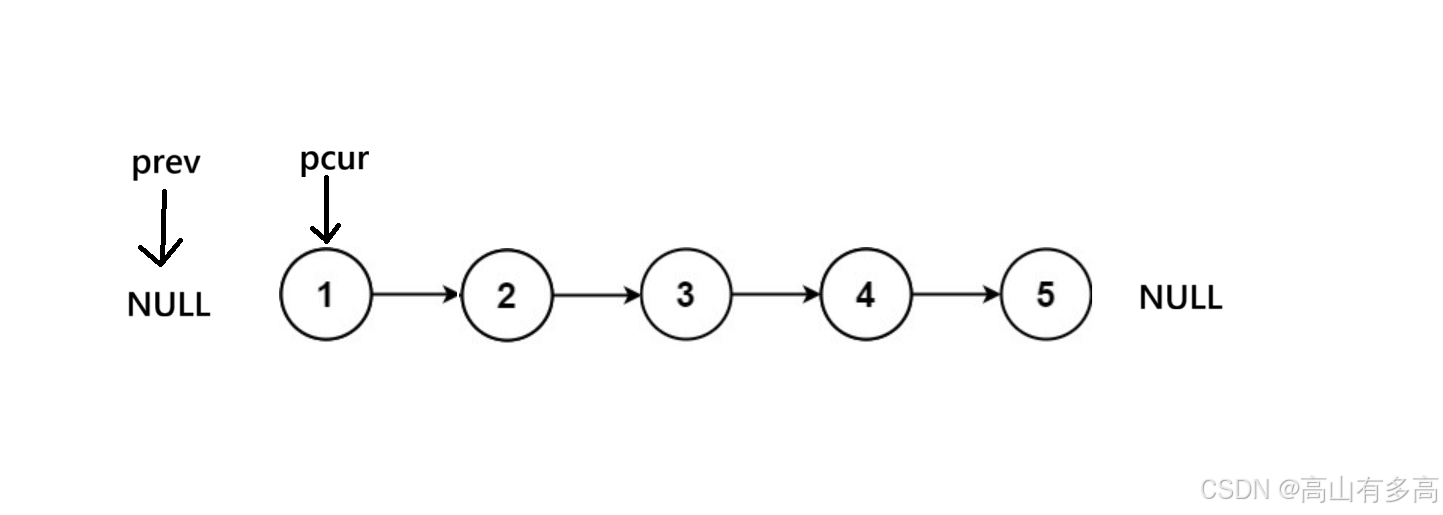
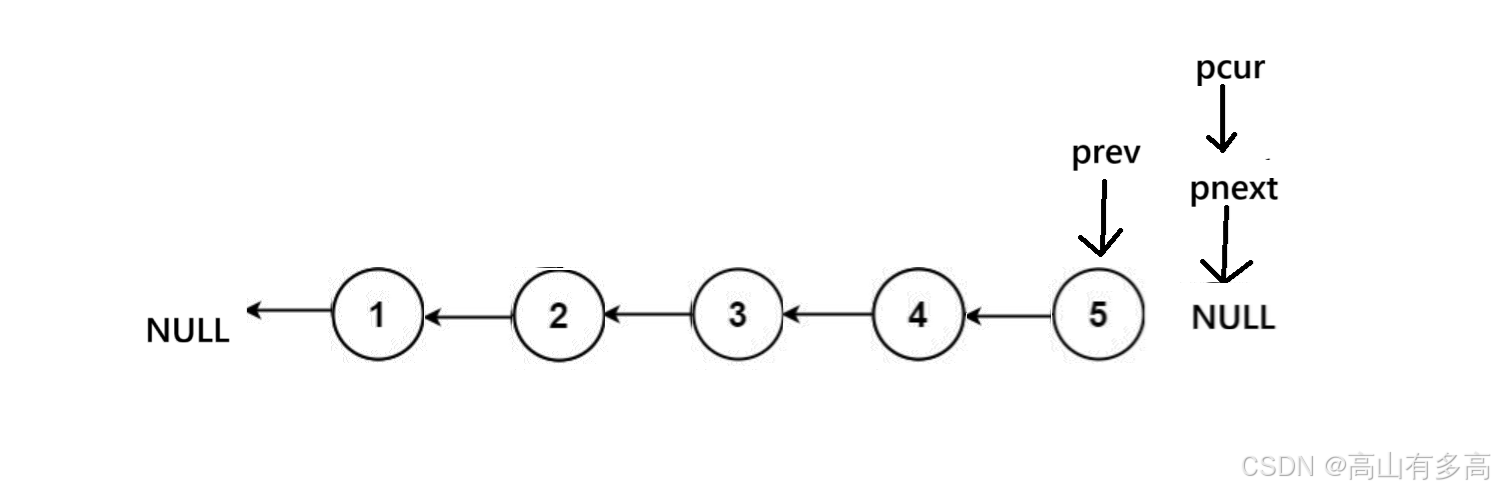
①定义三个指针变量，prev前驱指针，pcur当前指针，pnext用于临时保存pcur的下一个节点

        

②重点关注pcur指针和prev指针的走向，pnext只是用来临时保存pcur的下一个节点

        

1.首先，原本初始化之后是这样的， prev 指向 NULL， pcur 指向head。 我们要明确一点，我们交换的对象只有两个 pre 和 cur。

        

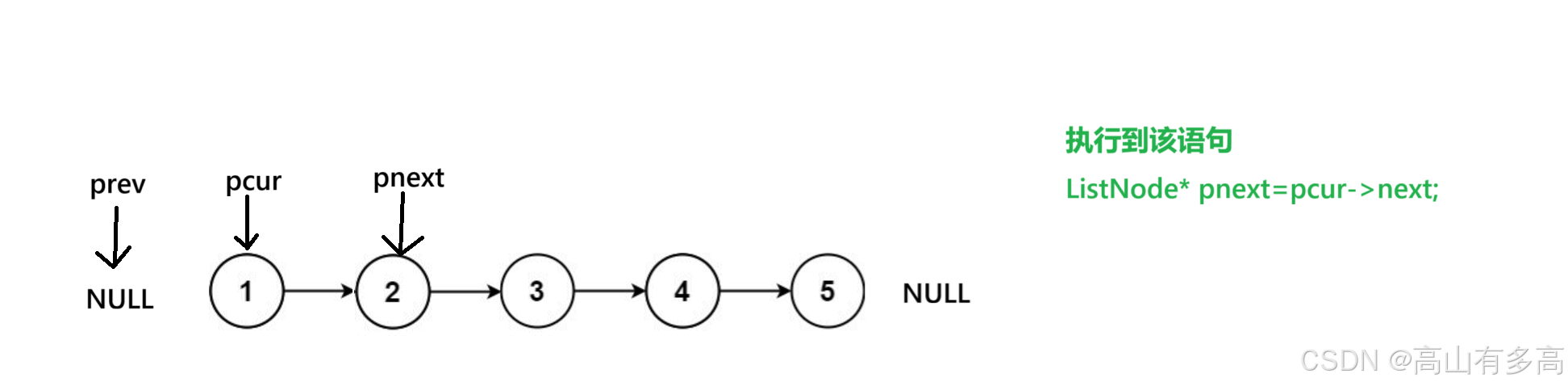
2.第二步，我们定义好pnext节点，我们不会对pnext节点有任何操作，它就像一个锚点，帮助我们临时保存pcur的下一个节点而已。

       

        

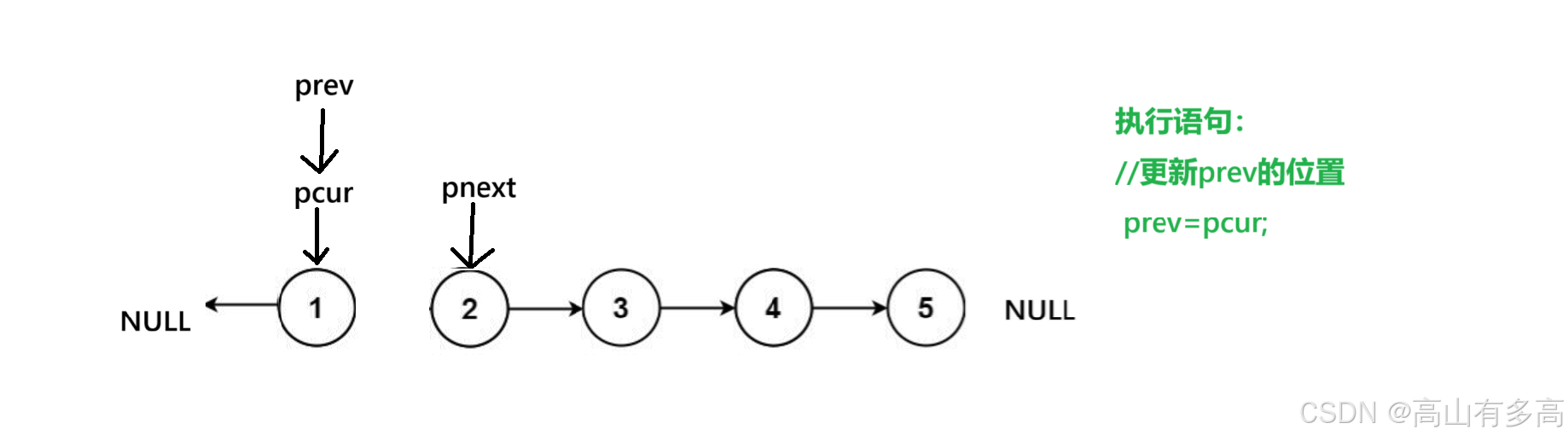
3.第三步，我们将当前pcur所指向的节点进行反向，执行最核心的反转步骤

        

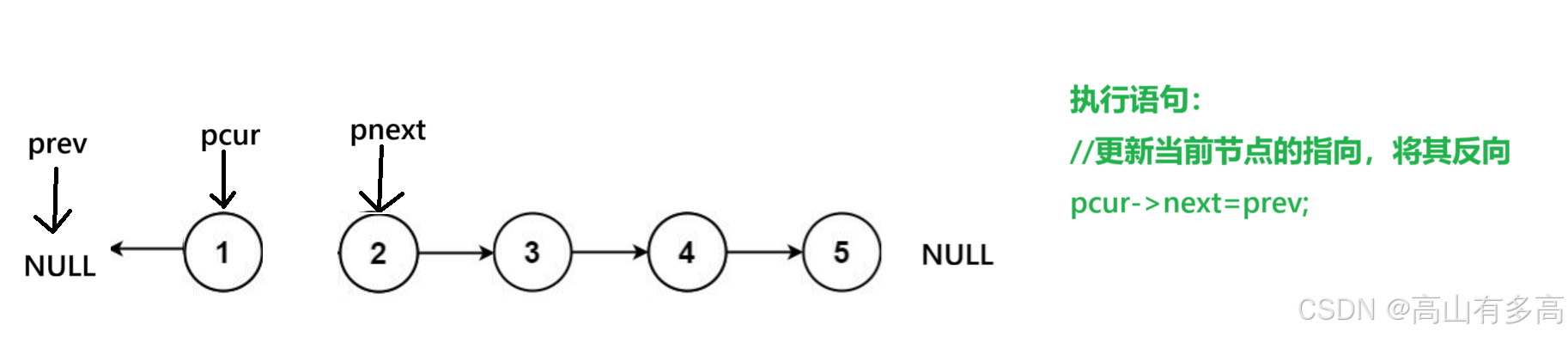
4.第四步，这里我们必须先移动 pre 再移动 cur。 不然会丢失节点位置

        

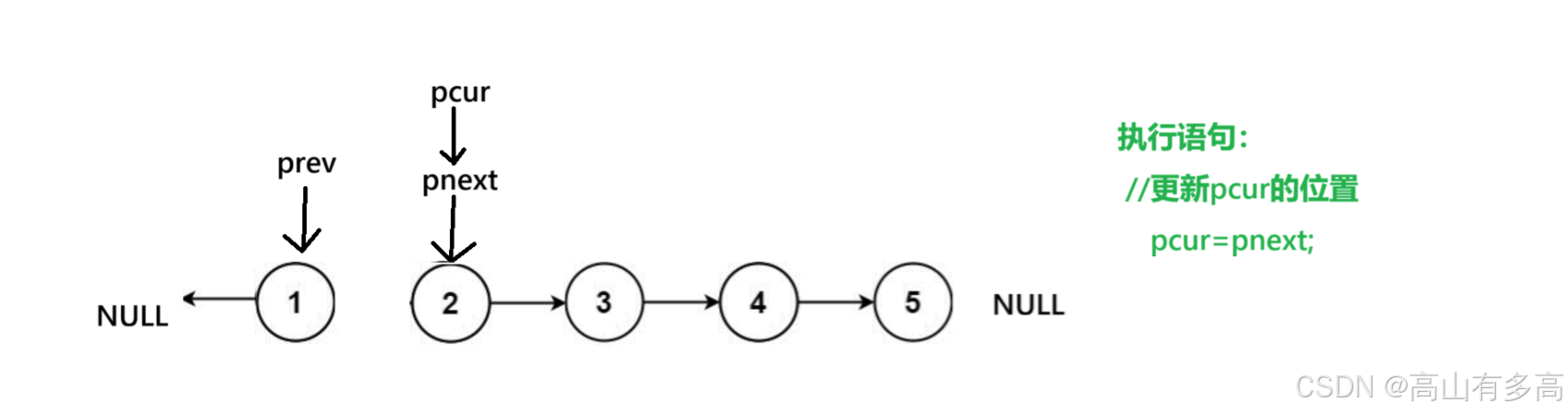
5.第五步，我们更新pcur位置，第一个循环结束。

        

        

6.以此类推，最后，判断循环结束条件，即当pcur指向为空时，循环退出。

        

2.2代码实现

思路一代码：

typedef struct ListNode ListNode ;
struct ListNode* reverseList(struct ListNode* head) 
{

    //新链表的头节点（初始为空）
    ListNode*newhead=NULL;

    //遍历原链表的指针
    struct ListNode* pcur=head;

    while(pcur)
    {
        //保存当前节点的下一个节点
        ListNode * pnext=pcur->next;
        //头插节点
         pcur->next=newhead;
        //更新头节点
        newhead=pcur;
        //更新当前节点
        pcur=pnext;
    }


    return newhead; 
}

        

思路二代码：

typedef struct ListNode ListNode;
struct ListNode* reverseList(struct ListNode* head) 
{
   ListNode * prev=NULL;
   ListNode * pcur=head;
   ListNode * pnext=head;
   while(pcur)
   {
    //保存当前节点的下一个节点指针
     pnext=pcur->next;
     //反转当前节点的指向（指向prev）
     pcur->next=prev;
     //更新prev的位置
     prev=pcur;
     //更新pcur的位置
     pcur=pnext;
   }
   return prev;
}

2.3优化与复盘

通过这道算法题我们了解了迭代的思想：

        

①保存后继节点：用 pnext 指针暂存当前节点 pcur 的下一个节点（pnext = pcur->next），防止修改 pcur 的指向后丢失后续链表。  

         

②反转指向：将当前节点 pcur 的 next 指针反向指向其前一个节点 prev（pcur->next = prev），这是 “反转” 的直接操作。        

        

③移动指针：将 prev 移动到 pcur 的位置（prev = pcur），pcur 移动到之前保存的 pnext 位置（pcur = pnext），为下一次反转做准备。

        

三、合并两个有序链表

 Leetcode链接：合并两个有序链表

题目描述：

​

        

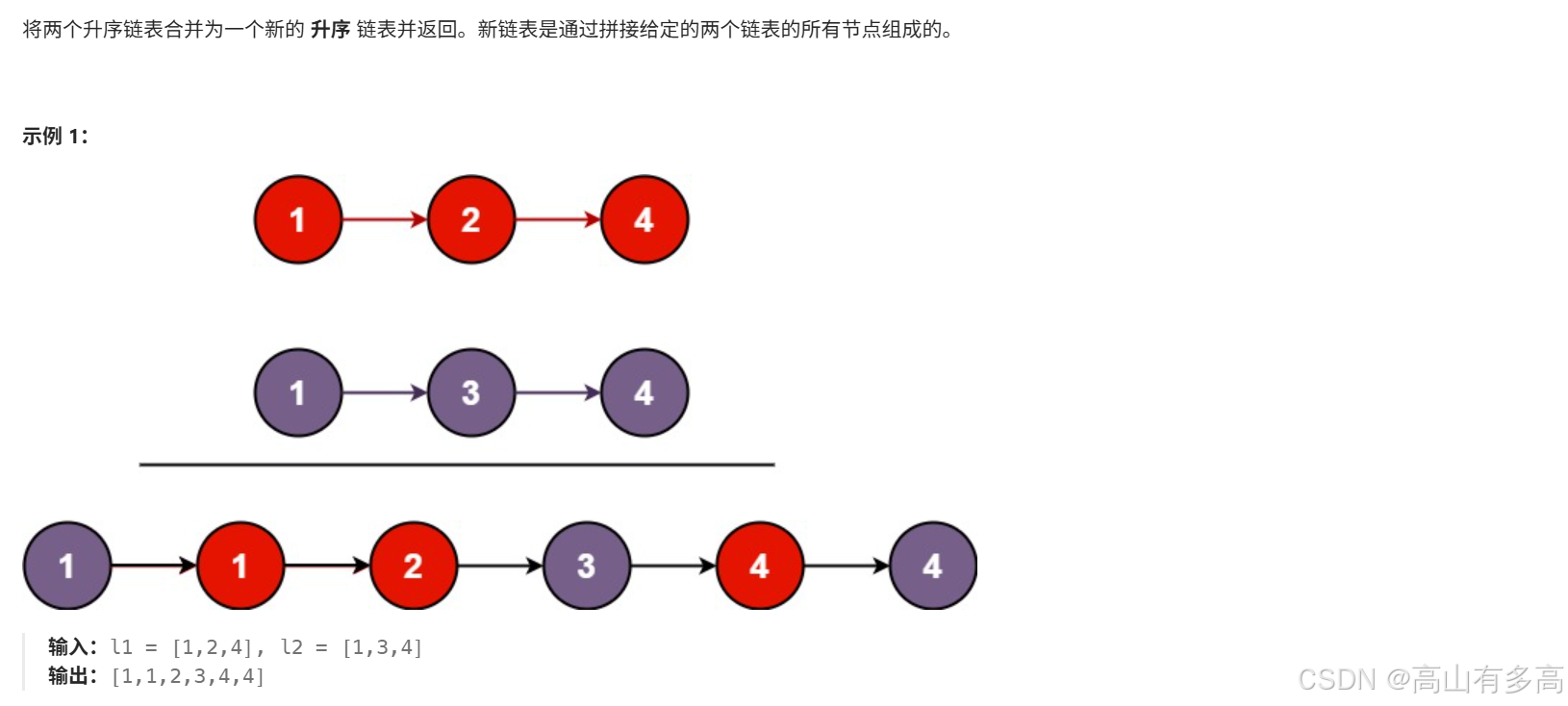
3.1题目思路剖析

核心思路：

①创建一个哨兵节点，作为合并后的新链表头节点的前一个节点。这样可以避免单独处理头节点，也无需特判链表为空的情况，从而简化代码。

        

②比较 list 1  和 list 2的节点值，如果 list 1的节点值小，则把 list 1 加到新链表的末尾，然后把 list 1替换成它的下一个节点。如果 list 2 的节点值小则同理。如果两个节点值一样，那么把谁加到新链表的末尾都是一样的，不妨规定把 list 2加到新链表末尾。

        

③重复上述过程，直到其中一个链表为空。循环结束后，其中一个链表可能还有剩余的节点，将剩余部分加到新链表的末尾。

        

④最后，返回新链表的头节点，即哨兵节点的下一个节点。

        

        

简而言之：

①定义两个指针p分别为p1和p2，用p1遍历第一个链表，用p2遍历第二个链表。

        

②创建一个新链表，根据p1->val 和 p2->val 值的比较，进行尾插到新链表中。

        

③处理剩余的节点，当p1优先遍历完第一个链表，直接尾插p2剩余的节点。反之，当p2优先遍历完第二个链表，直接尾插p1剩余的节点。 

        

3.2代码实现

typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2)
{
    ListNode * dummy=(ListNode *)malloc(sizeof(ListNode));  //哨兵位
    ListNode * ptail=dummy;
    dummy->next=NULL;
    ListNode * p1=list1;
    ListNode * p2=list2;
    
    while(p1&&p2)
    {
        if(p1->val >= p2->val)
        {
            //进行对p2尾插
            ptail->next=p2;
            p2=p2->next;
        }
        else
        {
            ptail->next=p1;
            p1=p1->next;
        }
        ptail=ptail->next;
    }
    //p2走到空
    if(p1)
    { 
        ptail->next=p1;
    }
    //p1走到空
    if(p2)
    {
        ptail->next=p2;
    }
    
    ListNode * newHead =dummy->next;
    free(dummy);
    dummy=NULL;

    return newHead;
}

        

3.3优化与复盘

通过这道题，我们加深理解了哨兵位的创建，以及对于链表尾插操作进一步深化。        

        

四、链表的中间节点

 Leetcode链接：链表的中间节点

题目描述：

        

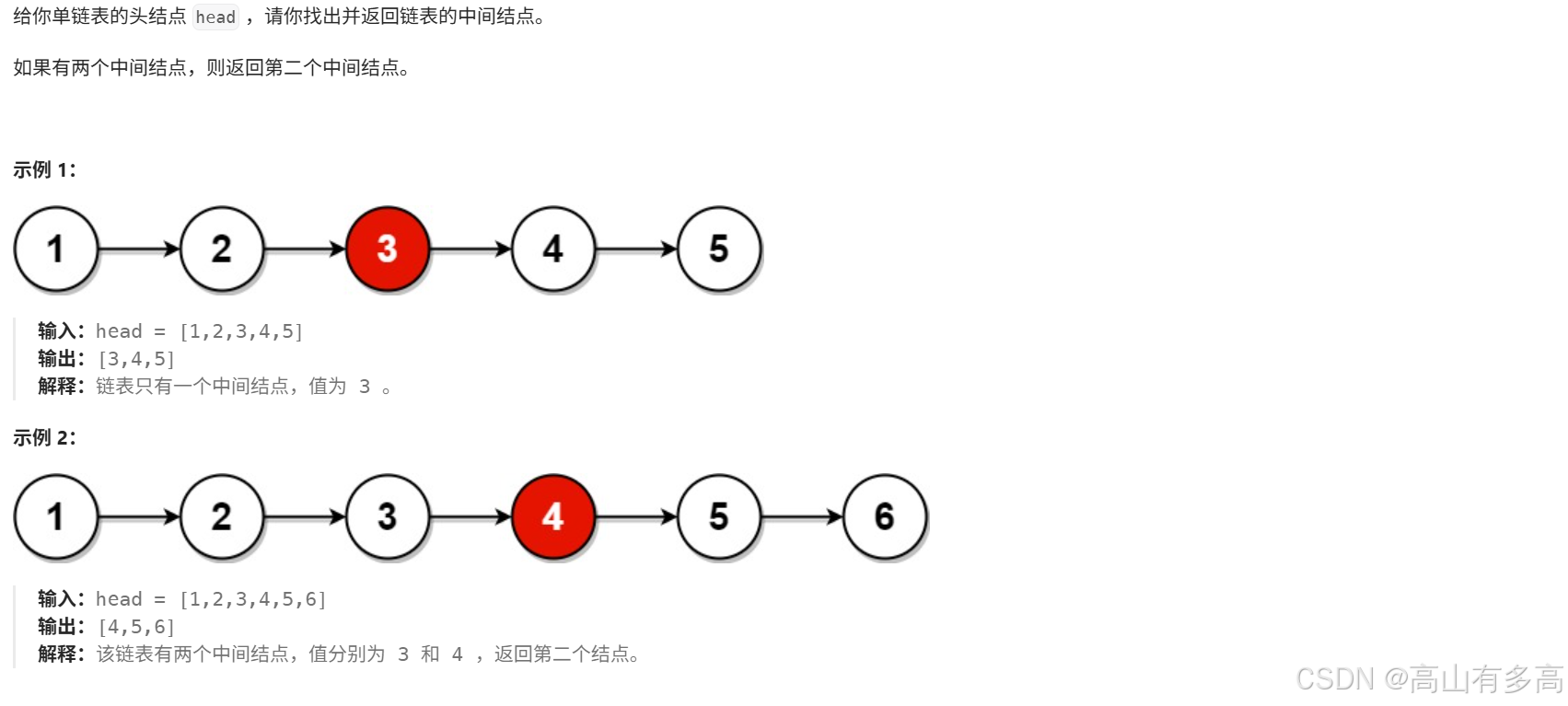
4.1题目思路剖析

这道题初看并没有什么思路，但如果将单链表视为数组的化，是不是类似于二分查找了？

        

如果我们采用数组的方式，遍历单链表中的每个节点，将链表每个节点的元素存入，这样是不是过于麻烦了。   

        

---

        

接下来我们将介绍一个极其巧妙的方法：快慢指针法，将极大优化代码量。

        

类似于百米跑步，甲乙两个同学，甲同学1s跑10m，乙同学1s只能跑5m，当甲跑完整个100m时，乙同学才跑完100m的一半，类比这个思想，我们就可以使用快慢指针，一个指针一次遍历两个节点，一个指针一次遍历1一个节点。 

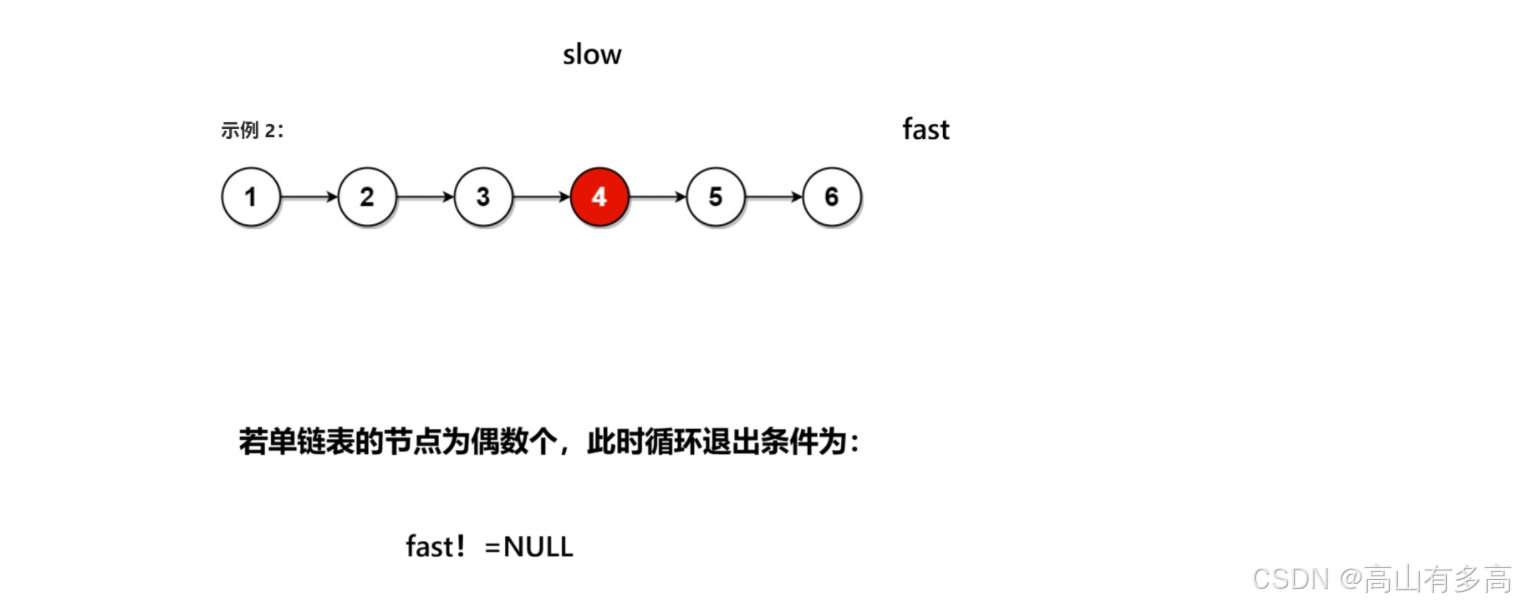
首先定义两个指针，一个快指针fast ，一个慢指针slow，让快指针一次遍历两个节点，让慢指针一次遍历一个节点，当快指针遍历完单链表时，是不是慢指针恰好在中间的位置。

        

4.2代码实现

typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head)
{
    //定义一个快指针和一个慢指针
    //快指针一次走两个节点，慢指针一次走一个节点，快指针走到尾节点，慢指针即走到中间
    ListNode * slow=head;
    ListNode * fast=head;
    while(fast && fast->next)
    {
        fast=fast->next->next;
        slow=slow->next;
    }
    return slow;

}

注意这里循环的结束条件：

        

①若单链表有奇数个节点

        

---

        

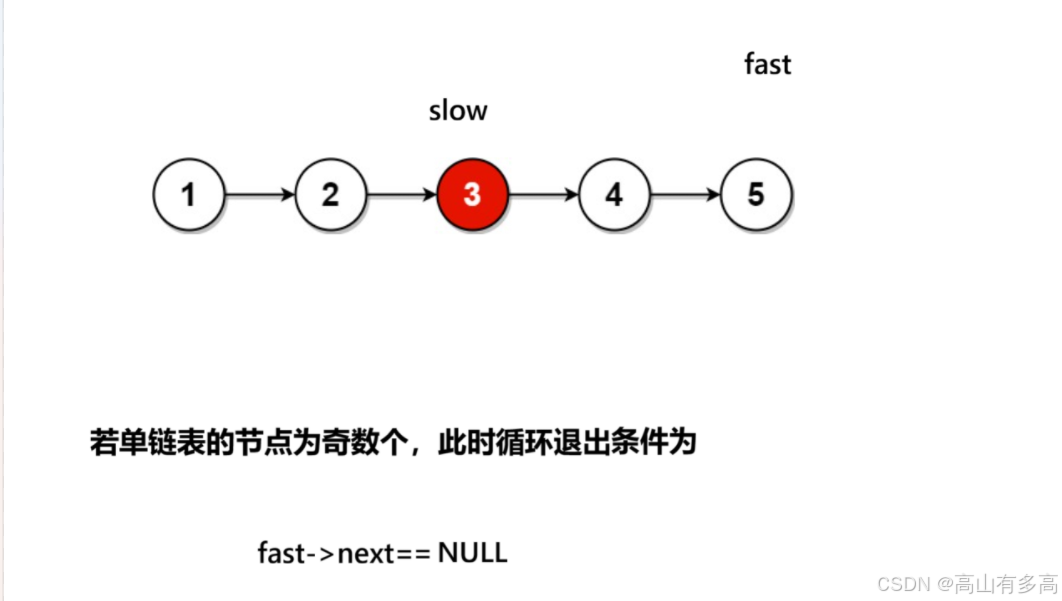
②单链表有偶数个节点

        

        

温馨提示：while(fast && fast->next) 不能改写为while( fast->next && fast)

        

如果是偶数个节点就会出现对空指针解引用，但如果写成while(fast && fast->next)会因为第一个条件为空而直接退出，不会判断第二个条件。

        

4.3优化与复盘

通过这道题，我们了解了对快慢指针的学习，进行运用    快指针=慢指针*2    这个公式。   

        

五、分割链表

Leetcode链接：分割链表

题目描述：

        

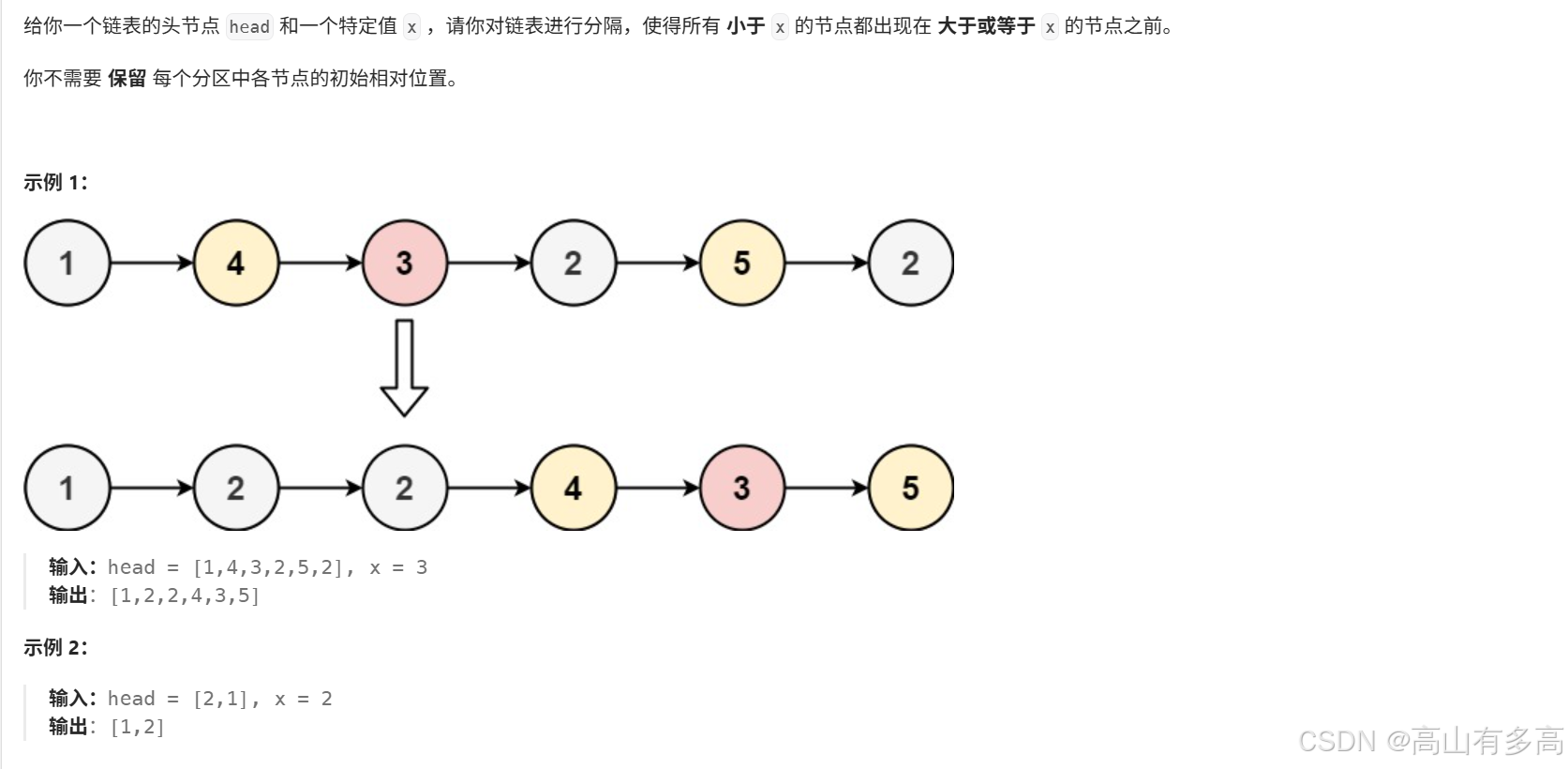
5.1题目思路剖析

思路解析：

        

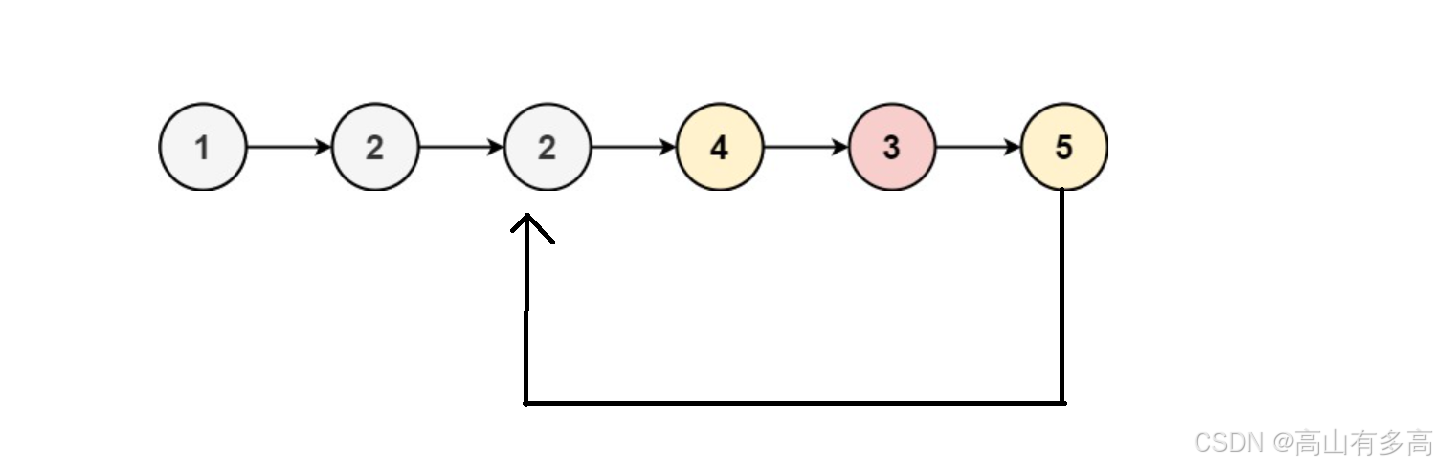
①通过定义两个空链表（创建两个哨兵位），一个链表存储小于等于x的值，记为small，另一个链表存储大于x的值，记为large。

        

②将smll链表的尾节点与large链表的头节点进行首尾相连。       

5.2代码实现

typedef struct ListNode ListNode;
struct ListNode* partition(struct ListNode* head, int x) 
{
    //定义两个链表，一个链表存储小于x，另一个链表存储大于x
    ListNode * small=(ListNode*)malloc(sizeof(ListNode));
    ListNode * large=(ListNode*)malloc(sizeof(ListNode));
    small->next=NULL;
    large->next=NULL;

    //存储小于x链表的尾节点
    ListNode * ptail1=small;

    //存储大于x链表的尾节点
    ListNode * ptail2=large;

    ListNode * pcur=head;
    while(pcur)
    {
        if(pcur->val>=x)
        {
            //尾插节点
            ptail2->next=pcur;
            //更新尾节点
            ptail2=ptail2->next;
        }
        else
        {
            ptail1->next=pcur;
            ptail1=ptail1->next;
        }
        pcur=pcur->next;
    }
    ptail2->next=NULL;
    ptail1->next=large->next;

    ListNode *ret=small->next;
    free(small);
    free(large);
    return ret;
}

5.3优化与复盘

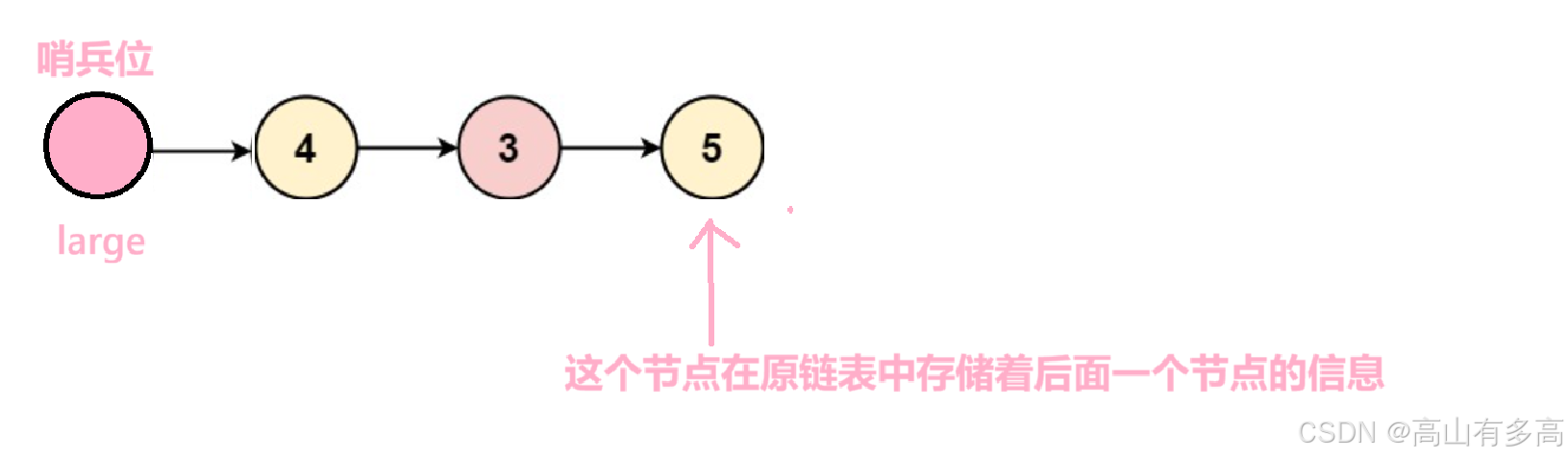
温馨提示：注意这段代码    ptail2->next=NULL;  对于存储大于x值的链表 的尾部要进行置空，否则有可能出现链表成环，导致无限死循环。

        

例如：

      

        

新创建的large链表尾节点存储着后一个节点的地址，如果不对其置空，small与large进行首尾相连时会出现环化。

        

如图所示：

        

六、环形链表的约瑟夫问题

牛客网链接：约瑟夫问题

题目描述：

        

6.1题目思路剖析

核心思路：

        

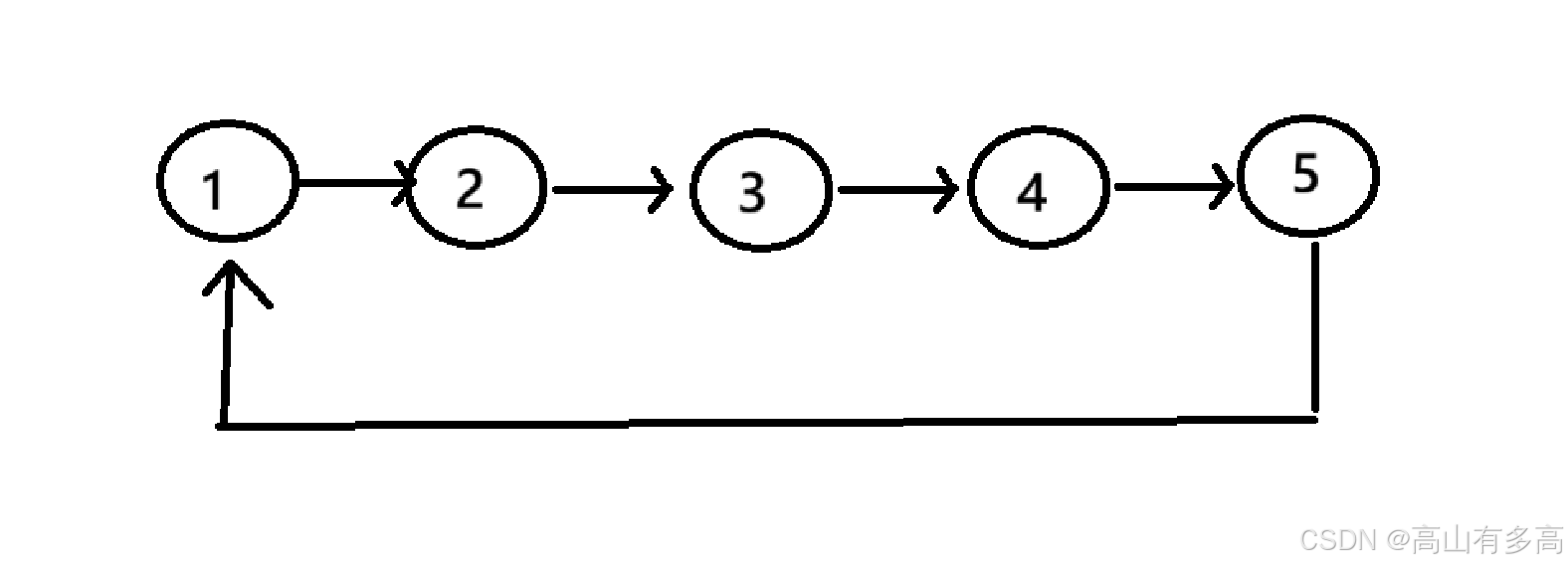
①通过进行模拟上述题目场景，进行创建循环链表，我们可以先定义一个单链表，将每个人的编号存入单链表的节点中，再将单链表的头节点和尾节点进行相连就可以形成一个循环链表。

        

如图所示：

       

        

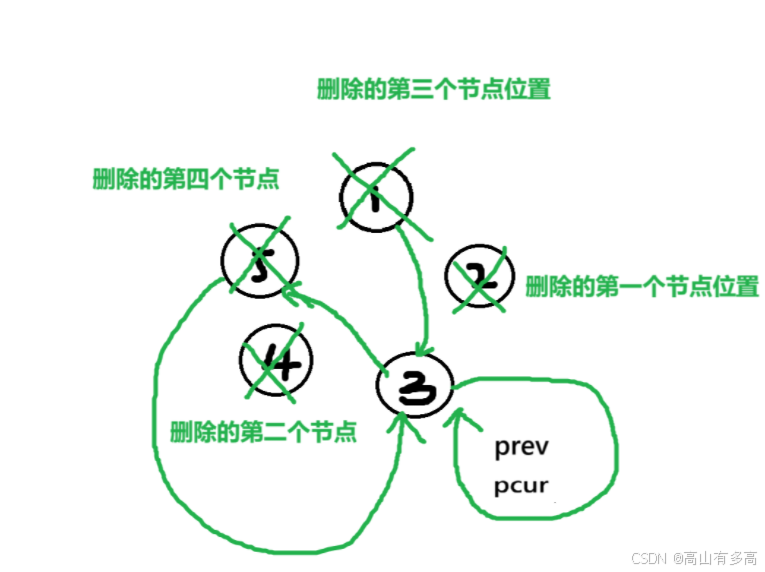
②定义一个计数器count，如果报数到m的节点进行删除，对于删除节点的方法，我们已经很熟悉了，先定义一个前驱指针prev，再定义一个pcur节点，prev先指向编号为5的节点，当前节点指向编号为1的节点，进行循环遍历。

 通过对其模拟可得

6.2代码实现

typedef struct ListNode ListNode ;

//创建一个节点
ListNode * setListNode(int x)
{
    ListNode * newnode=(ListNode *)malloc(sizeof(ListNode));
    if(newnode==NULL)
    {
        exit(1);
    }
    newnode->val=x;
    newnode->next=NULL;
    return newnode;
}

//创建循环链表
ListNode * Circlenode(int n)
{
    //头节点
    ListNode * phead=setListNode(1);
    //尾节点
    ListNode * ptail=phead;
    for(int i=2;i<=n;i++)
    {
        //尾插节点
        ptail->next=setListNode(i);
        //更新尾节点指针
        ptail=ptail->next;
    }
    //将第n个节点与头节点相连接
    ptail->next=phead;
    return ptail;
}

int ysf(int n, int m ) {
    // write code here
    //定义前驱节点
    ListNode * prev=Circlenode(n);
    //定义当前节点
    ListNode * pcur=prev->next;
    //定义计数器为1
    int count=1;
    while(pcur!=pcur->next)
    {
        //如果刚好报数到m，删除该节点
        if(count==m)
        {   
            //将前驱节点指向pcur的下一个节点
            prev->next=pcur->next;
            //释放当前节点
            free(pcur);
            //更新当前节点位置
            pcur=prev->next;
            //重置count
            count=1;
        }
         //如果报数不是m
        else
        {
           //更新前驱节点的位置
           prev=pcur;
           //更新当前节点的位置
           pcur=pcur->next;
           //更新count的值
           count++; 
        }

    }
    int ret=pcur->val;
    free(pcur);
    return ret;
}

6.3优化与复盘

注意事项一：

        对于创建完循环链表后，我们要将循环链表的尾节点进行返回，因为可以通过尾节点寻找得到头节点，如果返回环状链表的头节点，则找不到环状链表的尾节点，导致不能正确的定义前驱节点，和当前节点。

        

注意事项二：

        对于循环链表遍历完的退出条件为只剩下一个节点，即当前节点和当前节点的下一个节点不重合，pcur!=pcur->next, 。     

        

既然看到这里了，不妨点赞+收藏，感谢大家，若有问题请指正。