「少林派」多方安全计算

hellompc

于 2020-01-02 14:03:25 发布

阅读量390

点赞数 1

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/hellompc/article/details/103783212

本文介绍了秘密共享作为多方安全计算和联邦学习的基础应用技术，阐述其在密钥管理、数字签名等多个领域的关键作用。秘密共享通过分割秘密并分散存储，确保只有特定数量的参与者合作才能恢复秘密，提高系统的安全性和可靠性。此外，文章还提及不经意传输，一种保护接收者隐私的通信协议，使得发送者不知道接收者是否获取了信息。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

秘密共享

秘密共享(Secret-Sharing) 是现代密码学领域的一个重要分支，是信息安全和数据保密中的重要手段，也是多方安全计算和联邦学习等领域的一个基础应用技术。实际应用中，在密钥管理，数字签名，身份认证，多方安全计算，纠错码，银行网络管理以及数据安全等方面都有重要作用。

秘密共享是在一组参与者中共享秘密的技术，它主要用于保护重要信息，防止信息被丢失、被破坏、被篡改。它源于经典密码理论，最早由Sharmir和Blakley在1979年提出。简单来说，秘密共享就是指共享的秘密在一个用户群体里进行合理分配，以达到由所有成员共同掌管秘密的目的。

基于Shamir秘密共享理论的方法中，秘密共享的机制主要由秘密的分发者D、团体参与者P{P1，P2，…，Pn}、接入结构、秘密空间、分配算法、恢复算法等要素构成。

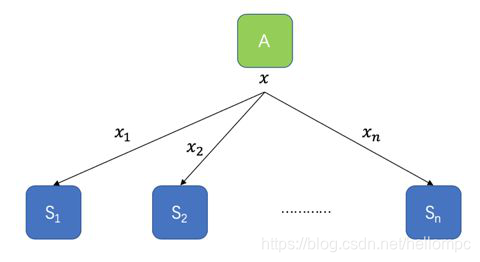
秘密共享通过把秘密进行分割，并把秘密在n个参与者中分享，使得只有多于特定t个参与者合作才可以计算出或是恢复秘密，而少于t个参与者则不可以得到有关秘密。如下图所示，特征A的值x，分割成x1，x2，……，xn，分发给S1，S2，……Sn。

秘密共享体系还具有同态的特性。如下图所示有特征A和B，他们的值被随机分成碎片(X1, X2, …, Xn)和(Y1, Y2, …, Y3)，并分配到不同参与节点(S1,S2, …, Sn)中，每个节点的运算结果的加和能等同于原始A与B的加和。同样通过增加其他计算机制，也能满足乘积的效果，这就是秘密共享具备的“同态性”，