Codeforces F. Maximum Weight Subset

题意：

n个节点的树，每个点有权值​，求满足点集内任两点间距离大于k的点集内的点权值和的最大值。

思路：

贪心解法：

贪心的选比较大的值。将所有点按照深度从小到大排序，如果当前点的点权大于0，则将距离为以内的所有点权减，代表了选择当前点，答案的贡献为。如果下面有扫到了点权大于0的点。说明取这个点的收益更大，于是取点，并将距离为以内的点权减。

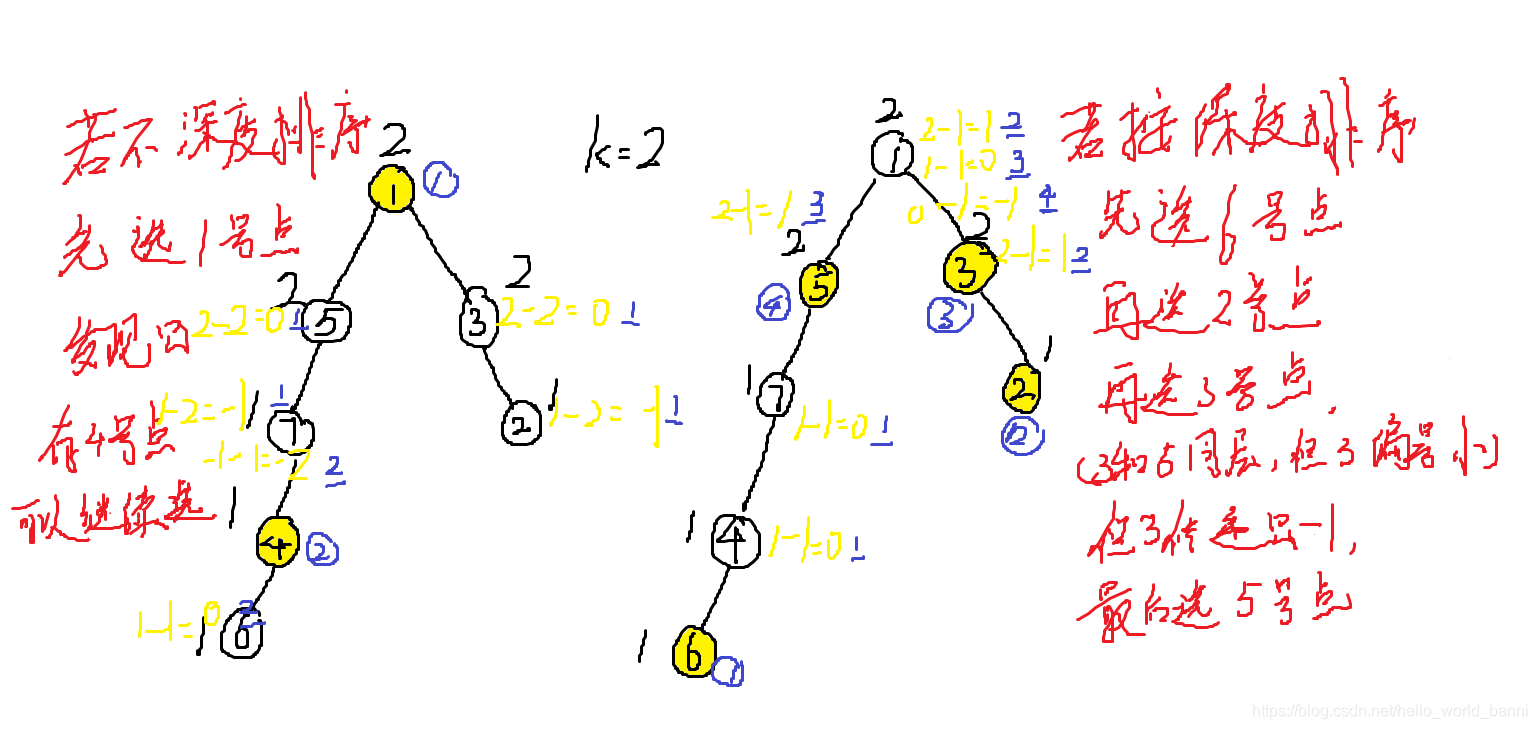
那么为什么要按照深度从小到大排序呢？以样例2为例：

注意每个传递的不是原始点权，而是减后的点权，表示的意思是：我可以增加的权值，但由于深度大的点有距离优势，所以我不一定选自己，传递的是如果选我，对上层节点的影响，也因此，我们要按节点的深度排序，因为此时就不用考虑下层节点了。保存的，就是最多能获得的点权和，即每一次​的变动，都是合法的。

 

#include<bits/stdc++.h>
using namespace std;
typedef pair<pair<int,int>,int> P;
#define mk make_pair
const int MAXN=1e5+5;
int a[MAXN];
int b[MAXN];
int dep[MAXN];
int res;
vector<int> g[MAXN];
void dfs(int u,int root,int i){//获得深度
    dep[u]=i;
    for(auto v:g[u]){
        if(v==root) continue;
        dfs(v,u,i+1);
    }
}
bool cmp(int x,int y){return dep[x]>dep[y];};//按深度排序
void deal(int x,int k){
    res+=a[x];
    int c=a[x];
    queue<P> que;
    que.push(mk(mk(x,-1),0));
    while(que.size()){
        P now=que.front();
        que.pop();
        int u=now.first.first;
        a[u]-=c;
        int root=now.first.second;
        int cnt_k=now.second;
        for(auto v:g[u]){
            if(v==root||cnt_k>=k) continue;
            que.push(mk(mk(v,u),cnt_k+1));
        }
    }
}
int main(){
    int n,k,u,v;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;b[i]=i,i++) scanf("%d",&a[i]);
    for(int i=1;i<n;i++){
        scanf("%d%d",&u,&v);
        g[u].push_back(v);g[v].push_back(u);
    }
    dfs(1,0,0);
    sort(b+1,b+n+1,cmp);
    for(int i=1;i<=n;i++)
        if(a[b[i]]>0) deal(b[i],k);
    printf("%d\n",res);
}