在数学与信号处理的领域中,一个实数值函数 的希尔伯特转换(Hilbert transform)——在此标示为
的希尔伯特转换(Hilbert transform)——在此标示为 ——是将信号
——是将信号 与
与 做卷积,以得到
做卷积,以得到 。因此,希尔伯特转换结果
。因此,希尔伯特转换结果 可以被解读为输入是
可以被解读为输入是 的线性非时变系统(linear time invariant system)的输出,而此一系统的脉冲响应为
的线性非时变系统(linear time invariant system)的输出,而此一系统的脉冲响应为 。这是一项有用的数学,用在描述一个以实数值载波做调制的信号之复数包络(complex envelope),出现在通讯理论(应用方面的详述请见下文。)
。这是一项有用的数学,用在描述一个以实数值载波做调制的信号之复数包络(complex envelope),出现在通讯理论(应用方面的详述请见下文。)
希尔伯特转换是以著名数学家大卫·希尔伯特(David Hilbert)来命名。
定义
希尔伯特转换定义如下:
其中
并考虑此积分为柯西主值(Cauchy principal value),其避免掉在 以及
以及 等处的奇点。
等处的奇点。
另外要指出的是:若 ,则
,则 可被定义,且属于
可被定义,且属于 ;其中
;其中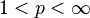 。
。
频率响应
希尔伯特转换之频率响应由傅立叶变换给出:
-
 ,
,
其中
 是傅立叶变换,
是傅立叶变换,- i (有时写作j )是虚数单位,
 是角频率,以及
是角频率,以及
即为符号函数。
既然:
-
 ,
,
希尔伯特转换会将负频率成分 偏移+90°,而正频率成分偏移−90°。
偏移+90°,而正频率成分偏移−90°。
反(逆)希尔伯特转换
我们也注意到: 。因此将上面方程式乘上
。因此将上面方程式乘上 ,可得到:
,可得到:
从中,可以看出反(逆)希尔伯特转换
特性
边界
若 1<p<∞,则 Lp(R)之希尔伯特转换为一有界算子,表示存在一常数Cp使得
对所有 u∈Lp(R)。这个定理由Riesz (1928, VII)所推得;请一并参见Titchmarsh (1948, Theorem 101)。 最佳常数Cp可由下列算式得到:
这个结果由(Pichorides 1972)所推得;请一并参见Grafakos (2004, Remark 4.1.8)。上述最佳常数计算方式应用在周期性希尔伯特转换一样成立。
希尔伯特转换的边界指的是 Lp(R) 对称级数运算子对于在 Lp(R) 之中 f 的收敛
请参见(Duoandikoetxea 2000,p.59)。
反自伴性
希尔伯特转换为一反自伴算子,连结 Lp(R) 与其对偶空间 Lq(R),其中 p 和 q 为 赫尔德共轭且 1 < p,q < ∞. 以符号表示
对 u ∈ Lp(R) 且 v ∈ Lq(R) (Titchmarsh 1948,Theorem 102).
逆转换
希尔伯特转换为一反-对合 (Titchmarsh 1948,p.120),意即
假定每一转换皆完整定义过。由于 H 保存了 Lp(R)空间,这特别代表希尔伯特转换在 Lp(R) 上是不可逆的,且
微分
正式上,一个式子其希尔伯特转换的微分即为其微分的希尔伯特转换,意即这两者是可以交换的线性算子
此一特性亦可迭代
给定 u 以及其前k次微分皆属于Lp(R) (Pandey 1996,§3.3)空间,此项论述为严格成立。在频域上可以轻易验证这件事情,由于微分在频域上即为与 ω 之乘积。
旋积
希尔伯特转换可表示为与一调节分布之旋积 (Duistermaat & Kolk 2010,p.211)
因此可如此表示
然而,事前此特性可能只有对紧支撑之分布 u定义。由于紧支撑函数在 Lp 上是稠密的,因此此项特性可能严格成立。另一角度来看,也可使用h(t) 其微分之特性来证明
在大部分的用途,希尔伯特转换可被视为是一旋积。举例而言,旋积与希尔伯特转换具备下列可交换的特性
若 u 和 v 为紧支撑分布,则此项论述严格成立,在这个状况下
不变性
希尔伯特转换在空间 L2(R) 上有下列特性
- 可与算子 Taƒ(x) = ƒ(x + a) 交换,对所有实数 a
- 可与算子 Mλƒ(x) = ƒ(λx) 交换,对所有 λ > 0
- 可与镜射 Rƒ(x) = ƒ(−x) 反交换
实际上,有更大一部分的算子可与希尔伯特转换交换。群组 SL(2,R) 由幺正算符 Ug 可在空间 L2(R) 上由以下式子表示
第一个程序效果如下





 本文介绍了希尔伯特变换的基本概念及其在数学与信号处理领域的应用。详细解释了变换的定义、频率响应、特性及实现原理,并通过MATLAB示例展示了变换过程。
本文介绍了希尔伯特变换的基本概念及其在数学与信号处理领域的应用。详细解释了变换的定义、频率响应、特性及实现原理,并通过MATLAB示例展示了变换过程。




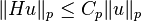





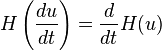
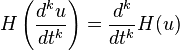



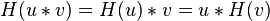



















 1500
1500

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








