动态规划-连续子数组的最大乘积

最新推荐文章于 2024-06-21 14:23:59 发布

原创最新推荐文章于 2024-06-21 14:23:59 发布 · 715 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法 #连续子数组乘积

刷题记录本专栏收录该内容

48 篇文章

订阅专栏

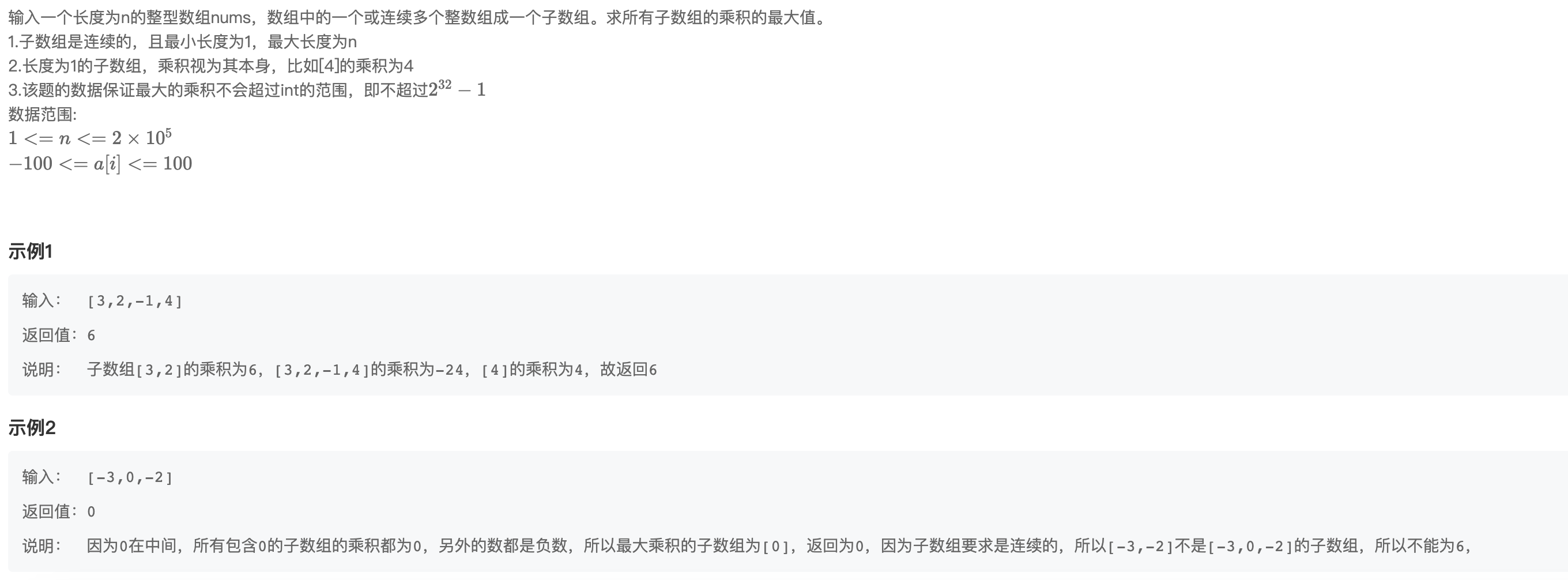
一、问题描述

二、解题思路

最大最小值都是在下面三种情况产生:

1.当前元素 nums[i]

2.前一个最大乘积*当前元素 maxArr[i-1]*nums[i]

3.前一个最小乘积*当前元素 minArr[i-1]*nums[i]

取最小值就是取三者中最小的，取最大值就是取三者中最大的

这里的最大最小值可以理解为：必须包含第i个元素时(相当于划定右侧范围)，前i个元素子数组最大最小值。

这里直接看不太好理解，举个例子来看一下：

nums = [3 , 2 -1 4]

maxArr: 3 6 -1 4

minArr: 3 2 -6 -24

初始情况下，maxArr[0]=3，minArr[0]=3；

当遇到nums[1]=2时，maxArr[1]=maxArr[0]*nums[1]；

当遇到nums[2]=-1时，maxArr[2]=nums[2]；minArr[2]=maxArr[1]*nums[2]；

当遇到nums[3]=4时，maxArr[3]=nums[3]；minArr[3]=minArr[2]*nums[3]；

三、代码实现

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param nums int整型一维数组 
     * @return int整型
     */
    public int maxProduct (int[] nums) {
        int maxRes=nums[0];
        int len=nums.length;
        //设置两个数组，记录当前最大、最小乘积
        int[] maxArr=new int[len];
        int[] minArr=new int[len];
        //最大最小值都是在下面三种情况产生:
        //(1)当前元素、(2)前一个最大乘积*当前元素、(3)前一个最小乘积*当前元素
        for(int i=0;i<len;i++){
            if(i==0){
                maxArr[0]=nums[0];
                minArr[0]=nums[0];
            }else{
                maxArr[i]=Math.max(Math.max(nums[i],maxArr[i-1]*nums[i]),minArr[i-1]*nums[i]);
                minArr[i]=Math.min(Math.min(nums[i],maxArr[i-1]*nums[i]),minArr[i-1]*nums[i]);
                maxRes=Math.max(maxArr[i],maxRes);
            }
        }
        //比如是nums=[3,2,-1,4]
        //maxArr:   3   6   -1  4
        //minArr:   3   2   -6  -24

        return maxRes;
    }
}