二叉平衡树（左单旋，右单旋，左右双旋、右左双旋）

原创已于 2024-07-10 21:01:12 修改 · 851 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#java #算法 #数据结构 #二叉平衡树 #AVL

于 2024-07-10 21:00:44 首次发布

数据结构与算法专栏收录该内容

13 篇文章

订阅专栏

一、AVL树（二叉平衡树：高度平衡的二叉搜索树）

0、二叉平衡树

左右子树高度差不超过1的二叉搜索树。

public class AVLTree{
    static class AVLTreeNode {
        public TreeNode left = null; // 节点的左孩子
        public TreeNode right = null; // 节点的右孩子
        public TreeNode parent = null; // 节点的双亲
        public int val = 0;
        public int bf = 0; // 当前节点的平衡因子=右子树高度-左子树的高度
        
        public TreeNode(int val) {
            this.val = val;
        }
    }
    public TreeNode root;

    //插入函数等....
    
}
// 将AVLTreeNode定义为AVLTree的静态内部类

1、查找

二叉平衡树的查找和二叉搜索树的方法是一样的，因为它们具有相同的结构特点——右孩子val值小于根节点val，根节点val小于左孩子val。

2、插入

二叉搜索树的插入一定是插入到叶子节点的位置。
二叉平衡树将节点插入到叶子节点之后，要维护左右子树的平衡因此可能还要进行旋转操作。

先将数据插入到AVL树当中（和二叉搜索数一样）
插入进去后，根据平衡因子来进行对树的调整

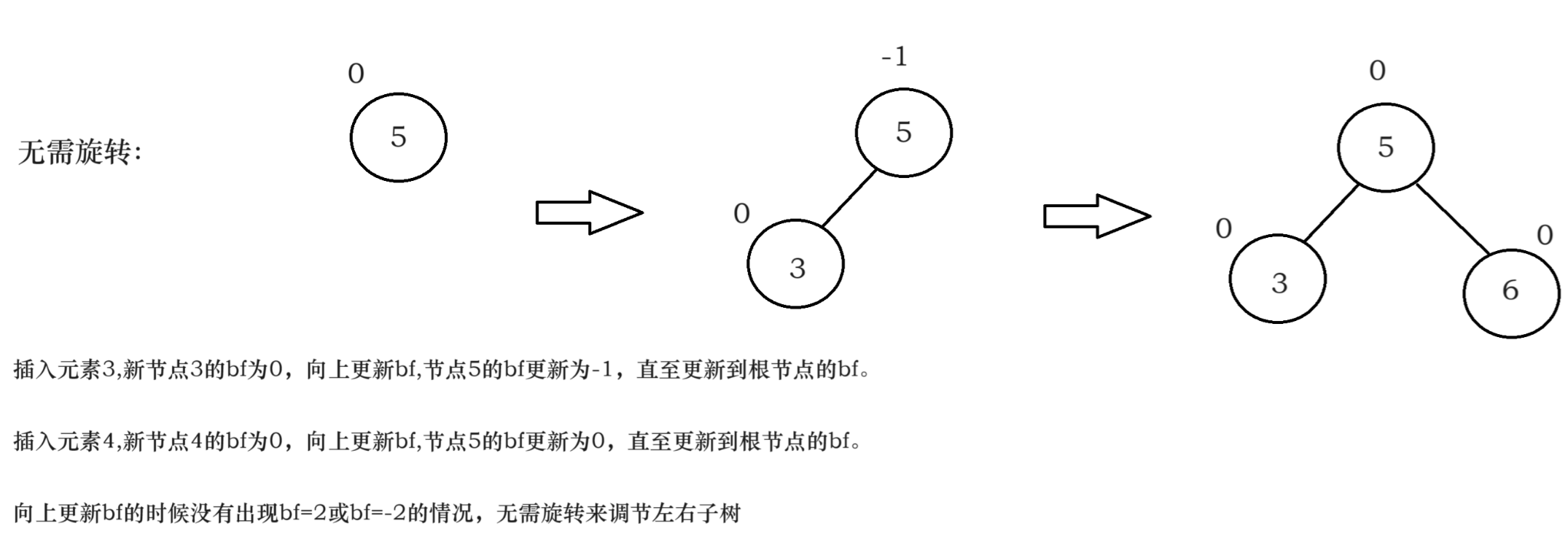
3、插入后无需旋转的情况：

注意各节点bf值得变化

4、右单旋&左单旋:

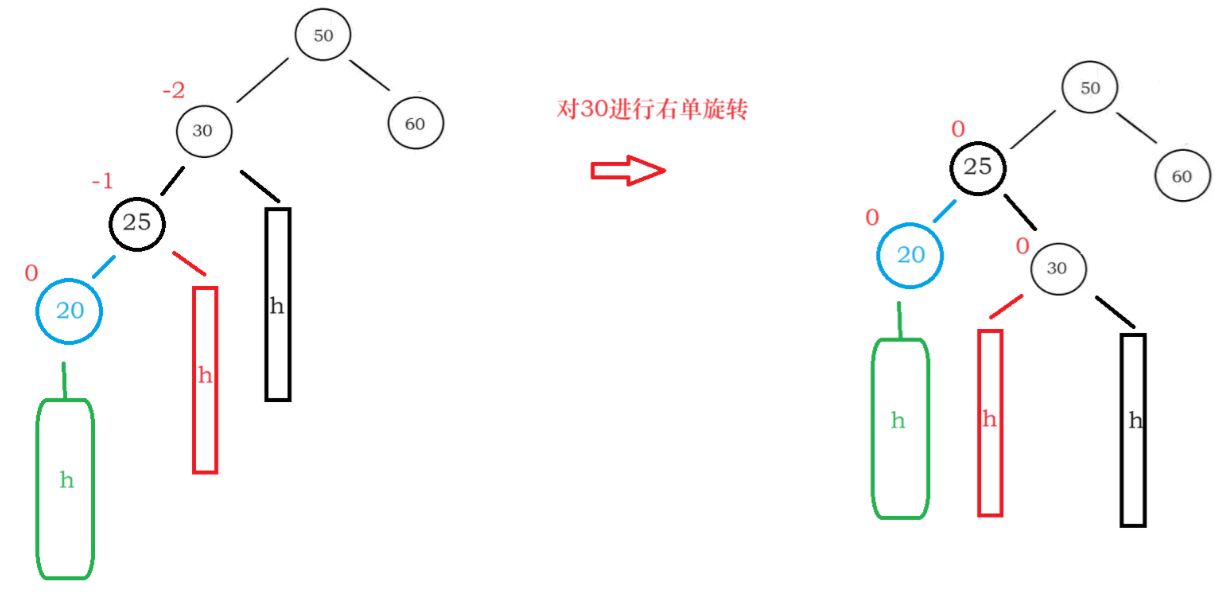
对parent进行右单旋就是把parent.left提拔成根节点
注意各节点bf值得变化

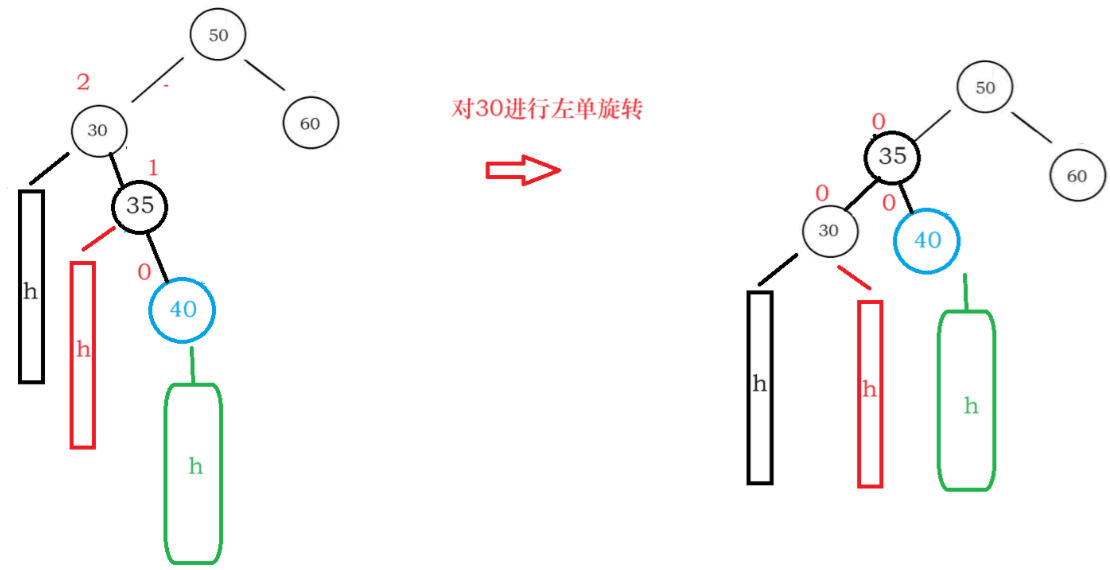
对parent进行左单旋就是把parent.right提拔成根节点
注意各节点bf值得变化

补充：相对与根节点各个节点的名称，后续得图会用到这些名称

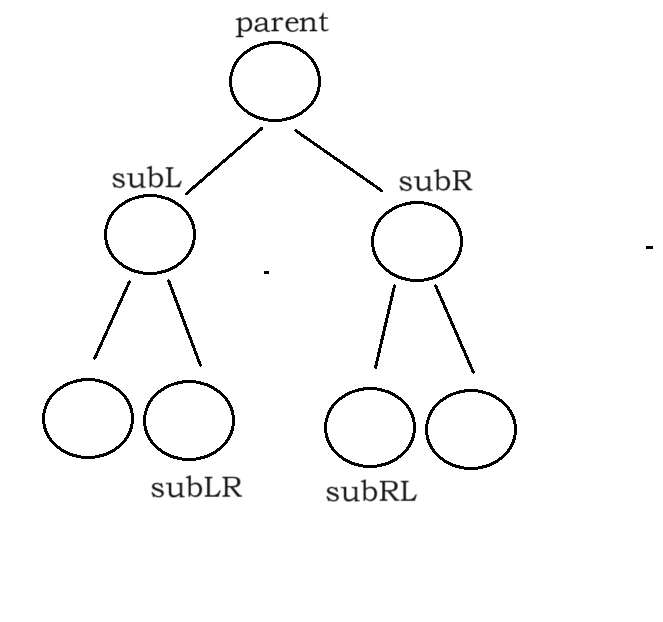
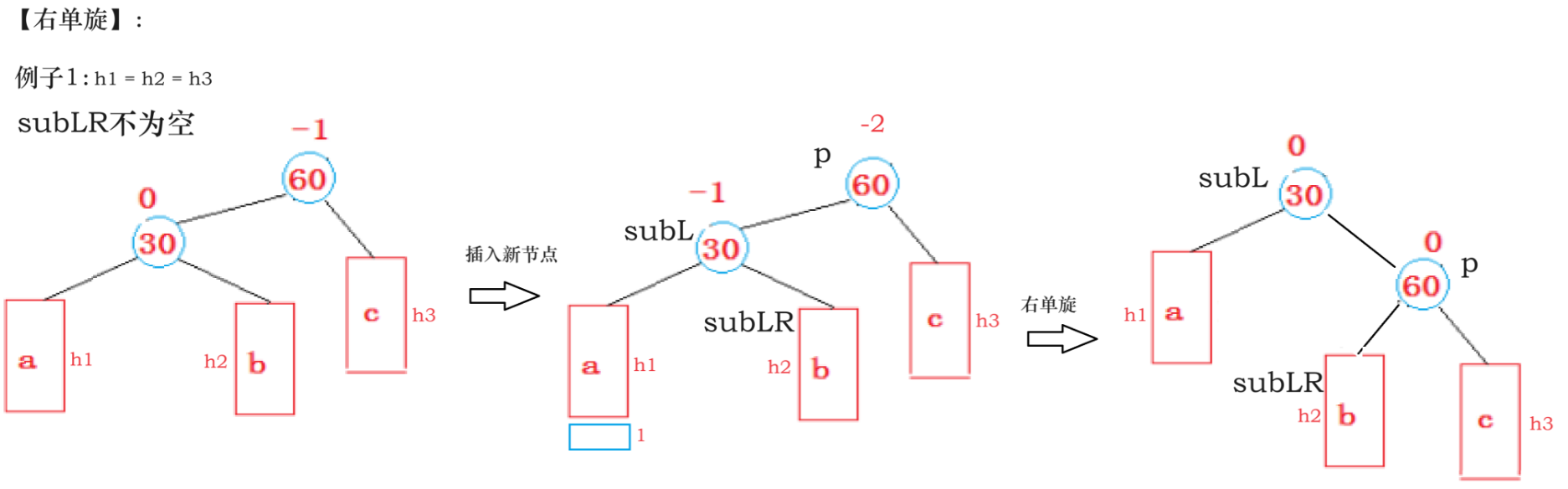
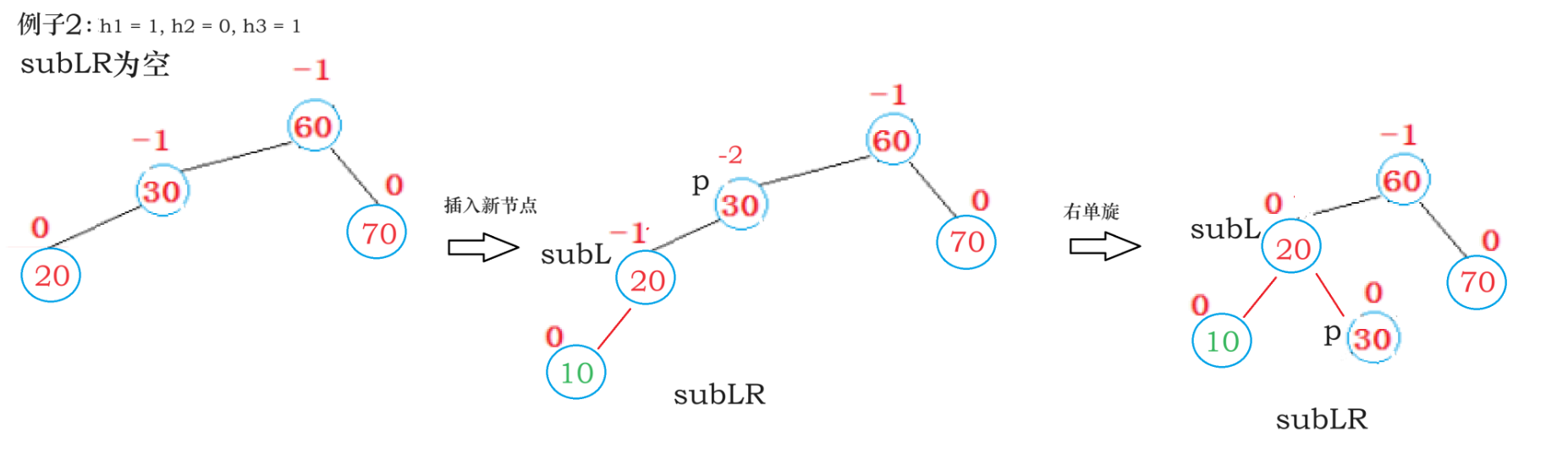
树parent是pParent(parent.parent)的一棵子树，对parent进行旋转后需要将新的根节点的parent指针指向pParent.

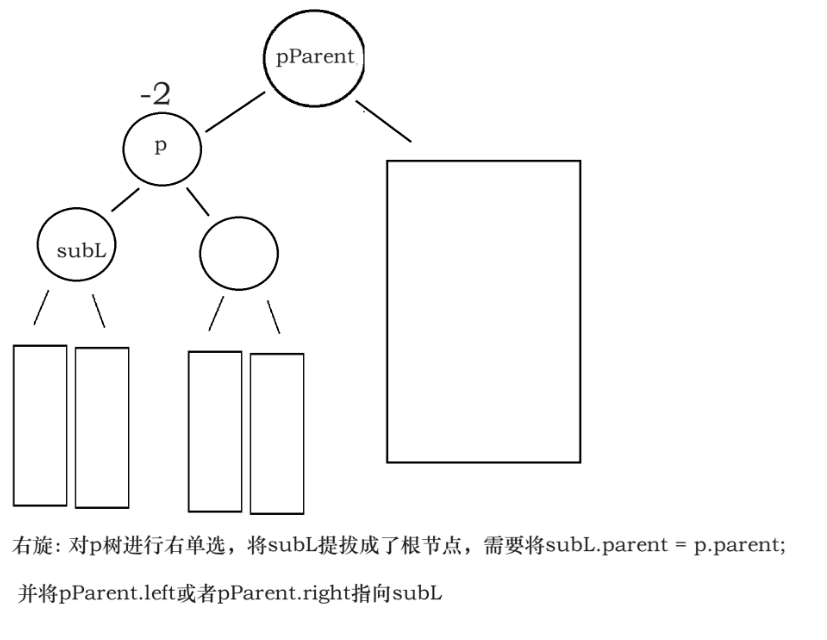
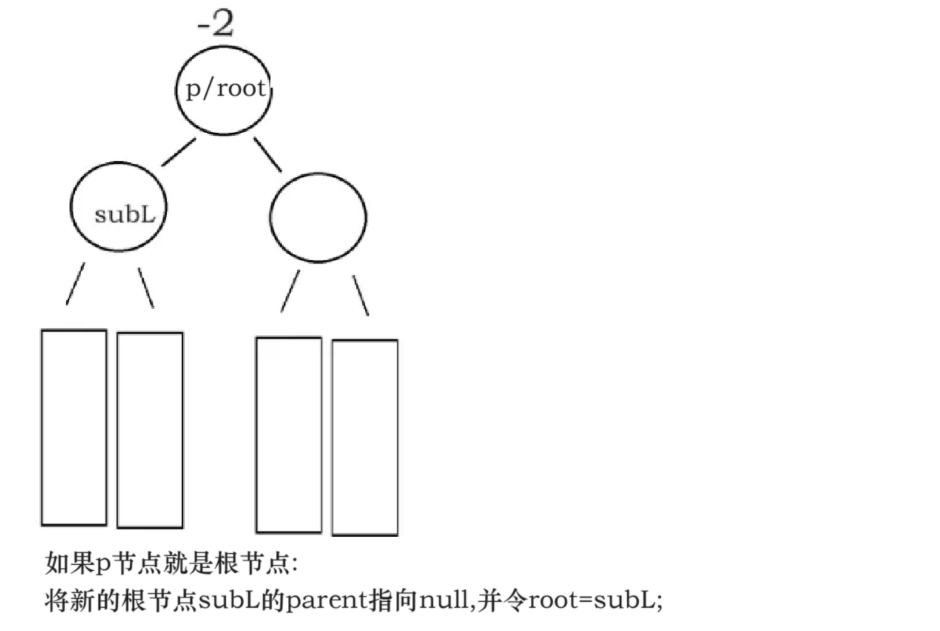
//检查 当前是不是就是根节点
if(parent == root) {
    root = subL;
    // subL.parent等于parent，subL提拔成了根节点，所以要将subL.parent设置为null,
    subL.parent = null;
}else {
    //不是根节点，判断这棵子树是左子树还是右子树
    if(pParent.left == parent) {
        pParent.left = subL;
    }else {
        pParent.right = subL;
    }
    subL.parent = pParent;
}

5、左右双旋 &右左双旋

注意指针指向
注意维护bf

右左双旋过程图：

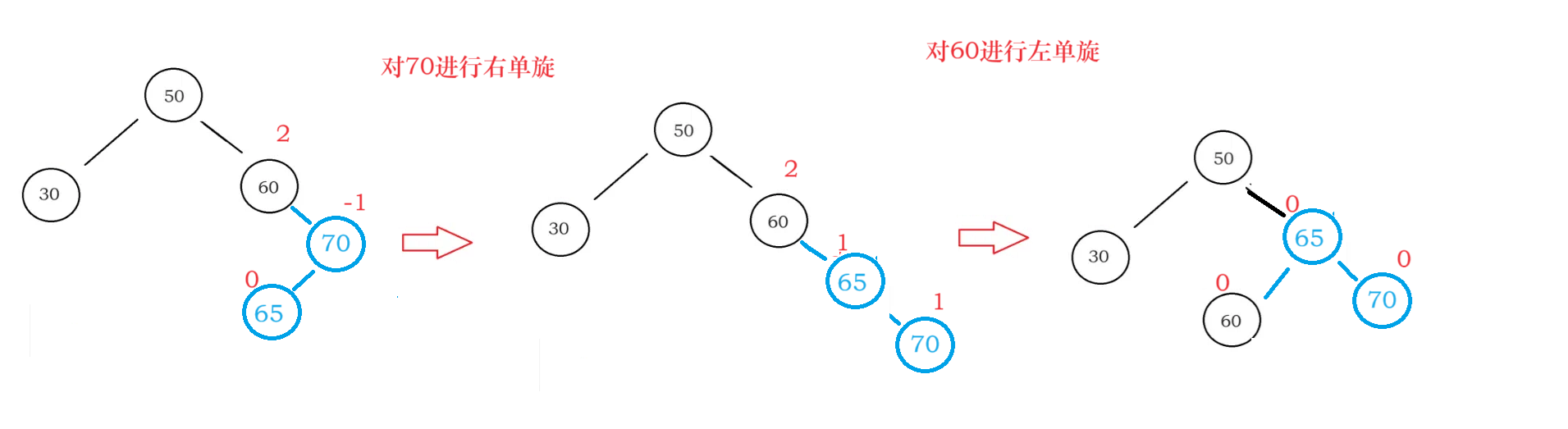
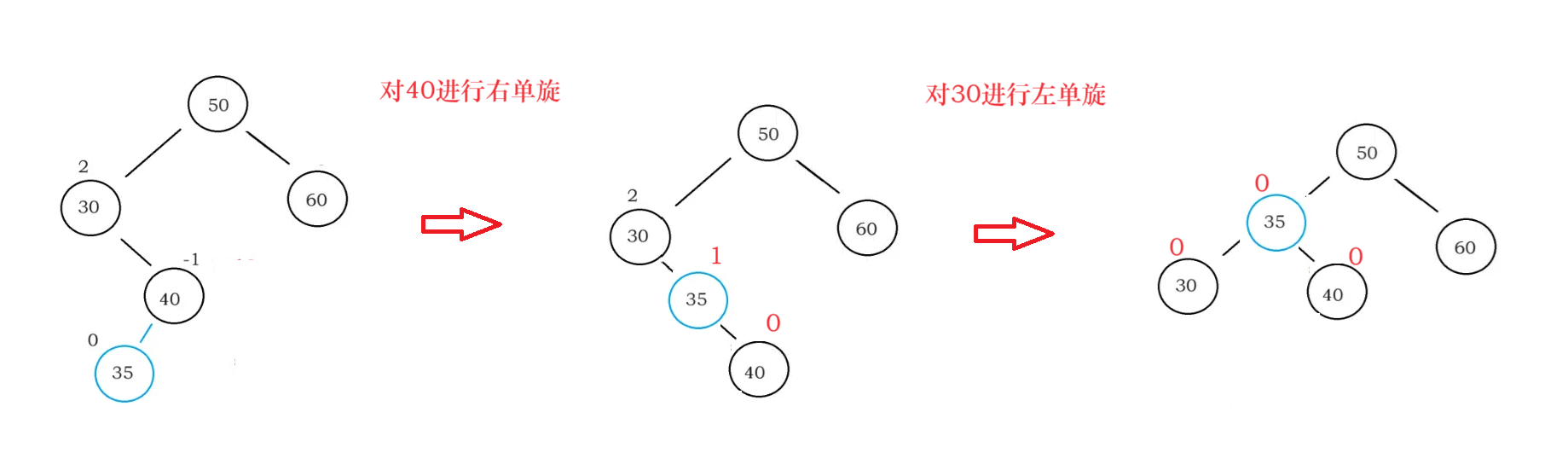
左右双旋过程图：

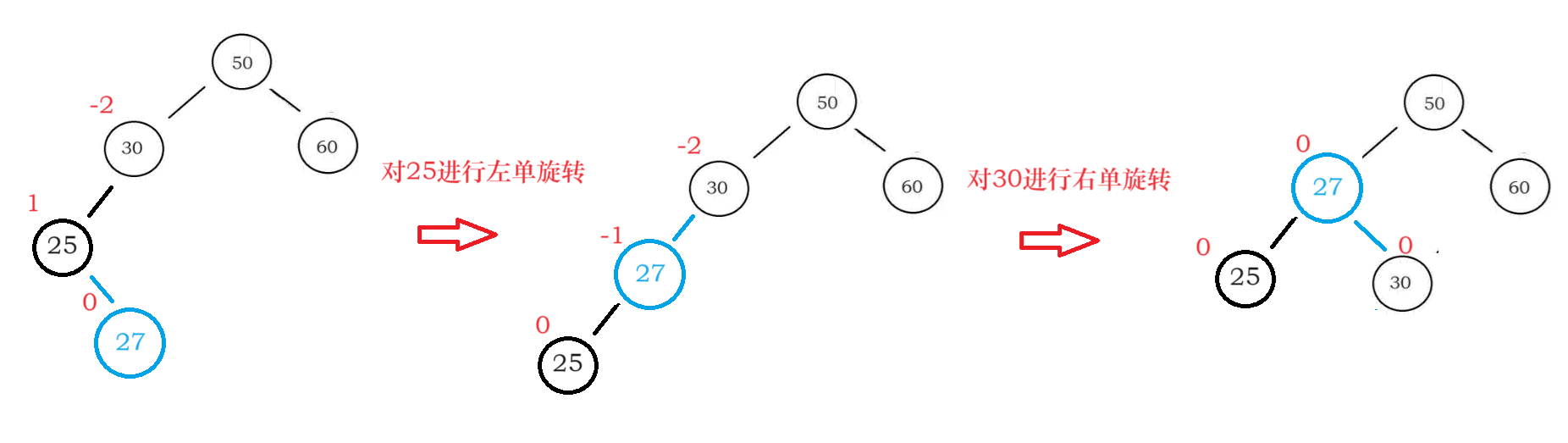
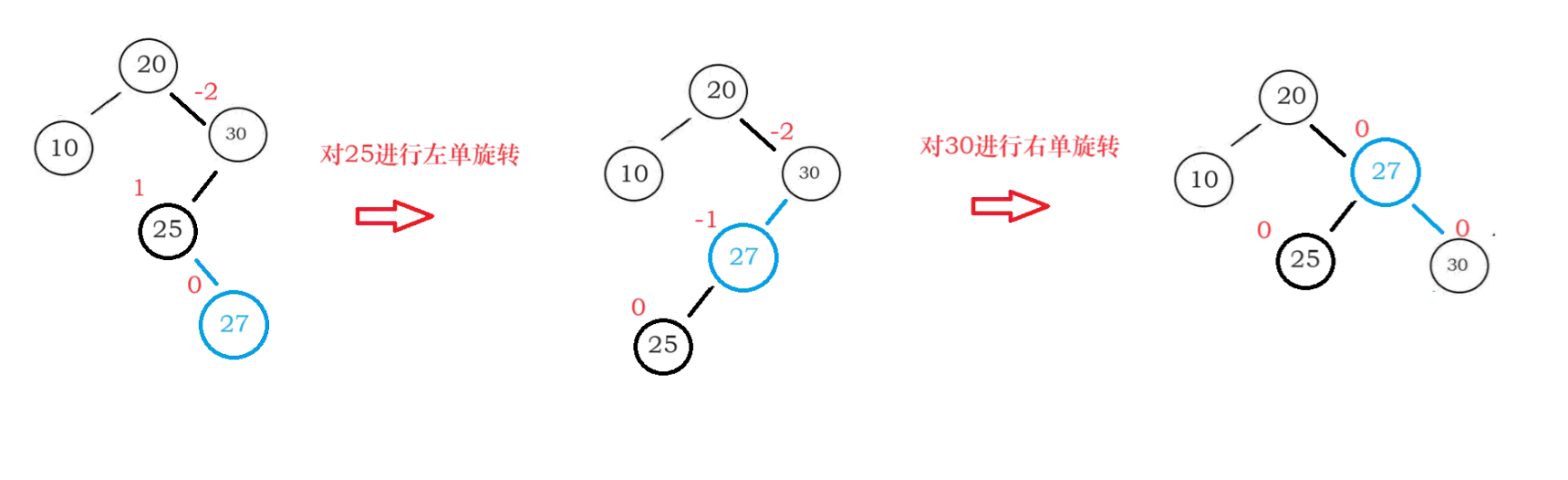
下面这两幅图介绍了左右双旋时如何维护个节点的bf值（右左双选的不想画了，太累了）

/**
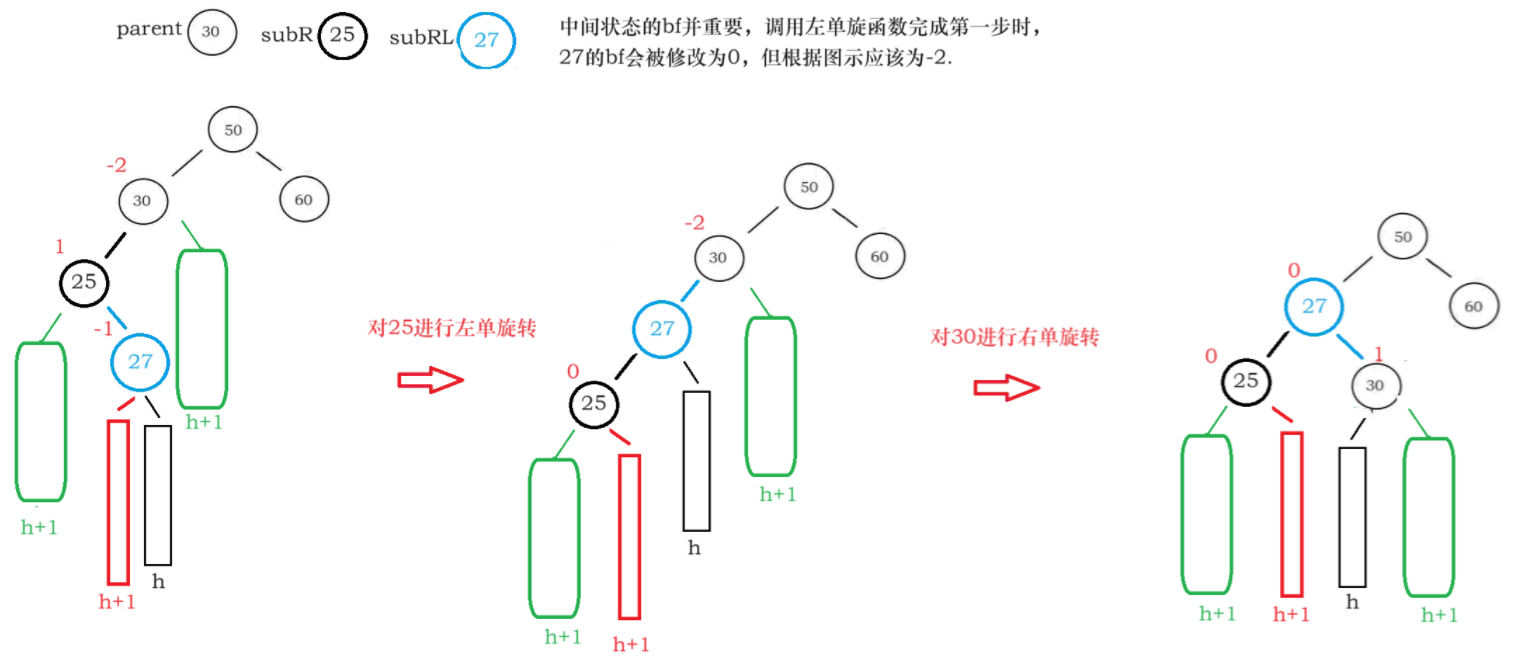
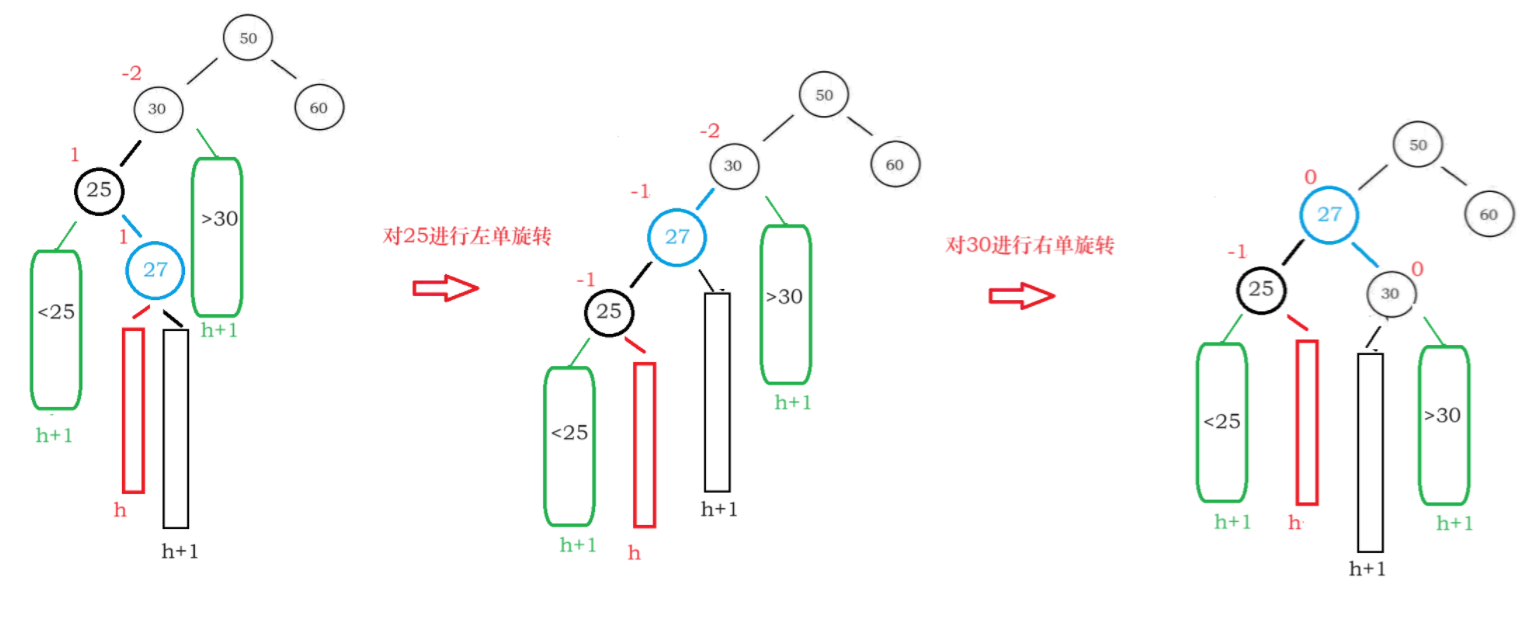
 * 左右双旋
 * @param parent
 */
private void rotateLR(TreeNode parent) {
    TreeNode subL = parent.left;
    TreeNode subLR = subL.right;
    int bf = subLR.bf;

    rotateLeft(parent.left);
    rotateRight(parent);

    // 这个规律很重要，中间状态的bf值不重要，根据初始状态的bf值来修改平衡状态的bf值
    if(bf == -1) {
        parent.bf = 1;
        subL.bf = 0;
        subLR.bf = 0;
    }else if(bf == 1){
        parent.bf = 0;
        subL.bf = -1;
        subLR.bf = 0;
    }
}

/**
 * 右左双旋
 * @param parent
 */
private void rotateRL(TreeNode parent) {
    TreeNode subR = parent.right;
    TreeNode subRL = subR.left;
    int bf = subRL.bf;
    
    rotateRight(parent.right);
    rotateLeft(parent);

    // 这个规律很重要，中间状态的bf值不重要，根据初始状态的bf值来修改平衡状态的bf值
    if(bf == 1) {
        parent.bf = -1;
        subR.bf = 0;
        subRL.bf = 0;
    }else if(bf == -1){
        parent.bf = 0;
        subR.bf = 1;
        subRL.bf = 0;
    }
}

6、总代码

package org.example;

/**
 * @Author 12629
 * @Description：
 */
public class AVLTree {
    static class TreeNode {
        public int val;
        public int bf;//平衡因子
        public TreeNode left;//左孩子的引用
        public TreeNode right;//右子树的引用
        public TreeNode parent;//父亲节点的引用

        public TreeNode(int val) {
            this.val = val;
        }
    }

    public TreeNode root;//根节点

    public boolean insert(int val) {
        TreeNode node = new TreeNode(val);
        if(root == null) {
            root = node;
            return true;
        }

        TreeNode parent = null;
        TreeNode cur = root;
        while (cur != null) {
            if(cur.val < val) {
                parent = cur;
                cur = cur.right;
            }else if(cur.val == val) {
                return false;
            }else {
                parent = cur;
                cur = cur.left;
            }
        }
        //cur == null
        if(parent.val < val) {
            parent.right = node;
        }else {
            parent.left = node;
        }
        //
        node.parent = parent;
        cur = node;
        // 平衡因子 的修改
        while (parent != null) {
            //先看cur是parent的左还是右  决定平衡因子是++还是--
            if(cur == parent.right) {
                //如果是右树，那么右树高度增加 平衡因子++
                parent.bf++;
            }else {
                //如果是左树，那么左树高度增加 平衡因子--
                parent.bf--;
            }

            //检查当前的平衡因子 是不是绝对值 1  0  -1
            if(parent.bf == 0) {
                //说明已经平衡了
                break;
            }else if(parent.bf == 1 || parent.bf == -1) {
                //继续向上去修改平衡因子
                cur = parent;
                parent = cur.parent;
            }else {
                //右树高-》需要降低右树的高度
                if(parent.bf == 2) {
                    if(cur.bf == 1) {
                        //左旋
                        rotateLeft(parent);
                    }else {
                        //cur.bf == -1
                        rotateRL(parent);
                    }
                }else {
                    //parent.bf == -2 左树高-》需要降低左树的高度
                    if(cur.bf == -1) {
                        //右旋
                        rotateRight(parent);
                    }else {
                        //cur.bf == 1
                        rotateLR(parent);
                    }
                }
                //上述代码走完就平衡了
                break;
            }
        }
        return true;
    }

    private void rotateRL(TreeNode parent) {
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;
        int bf = subRL.bf;

        rotateRight(parent.right);
        rotateLeft(parent);

        if(bf == 1) {
            parent.bf = -1;
            subR.bf = 0;
            subRL.bf = 0;
        }else if(bf == -1){
            parent.bf = 0;
            subR.bf = 1;
            subRL.bf = 0;
        }
    }

    /**
     * 左右双旋
     * @param parent
     */
    private void rotateLR(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        int bf = subLR.bf;

        rotateLeft(parent.left);
        rotateRight(parent);

        if(bf == -1) {
            parent.bf = 1;
            subL.bf = 0;
            subLR.bf = 0;
        }else if(bf == 1){
            parent.bf = 0;
            subL.bf = -1;
            subLR.bf = 0;
        }
    }

    /**
     * 左单旋
     * @param parent
     */
    private void rotateLeft(TreeNode parent) {

        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;

        parent.right = subRL;

        subR.left = parent;
        if(subRL != null) {
            subRL.parent = parent;
        }

        TreeNode pParent = parent.parent;
        parent.parent = subR;

        if(root == parent) {
            root = subR;
            root.parent = null;
        }else {
            if(pParent.left == parent) {
                pParent.left = subR;
            }else {
                pParent.right = subR;
            }
            subR.parent = pParent;
        }
        subR.bf = parent.bf = 0;
    }

    /**
     * 右单旋
     * @param parent
     */
    private void rotateRight(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        parent.left = subLR;
        subL.right = parent;
        //没有subLR
        if(subLR != null) {
            subLR.parent = parent;
        }
        //必须先记录
        TreeNode pParent = parent.parent;
        parent.parent = subL;
        //检查 当前是不是就是根节点
        if(parent == root) {
            root = subL;
            // subL.parent等于parent，subL提拔成了根节点，所以要将subL.parent设置为null.
            subL.parent = null;
        }else {
            //不是根节点，判断这棵子树是左子树还是右子树
            if(pParent.left == parent) {
                pParent.left = subL;
            }else {
                pParent.right = subL;
            }
            subL.parent = pParent;
        }
        subL.bf = 0;
        parent.bf = 0;
    }
    //中序遍历的结果是有序的 就能说明当前树 一定是AVL树吗？  不一定的
    private boolean inorder(TreeNode root){
        return inorderHelper(root,Long.MIN_VALUE);
    }
    private boolean inorderHelper(TreeNode root,long pre) {
        if(root == null) {
            return true;
        }
        if(!inorderHelper(root.left,pre)) {
            return false;
        }
        if(pre < root.val){
            pre = root.val;
            if(!inorderHelper(root.right,pre)){
                return false;
            }
            return true;
        }
        return false;
    }

    private int height(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int leftH = height(root.left);
        int rightH = height(root.right);

        return leftH > rightH ? leftH+1 : rightH+1;
    }

    public boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }
        int leftH = height(root.left);
        int rightH = height(root.right);

        if(rightH-leftH != root.bf) {
            System.out.println("这个节点："+root.val+" 平衡因子异常");
            return false;
        }

        return Math.abs(leftH-rightH) <= 1
                && isBalanced(root.left)
                && isBalanced(root.right)
                &&inorder(root);// 不仅要左右平衡，还要排序
    }
}

二叉平衡树的适用和不适用场景如下:
适用场景:

动态数据集合:
当需要频繁地对数据集合进行插入、删除和查找操作时,二叉平衡树是一个很好的选择。它能够保持O(log n)的时间复杂度,避免了普通二叉搜索树在极端情况下退化为链表的问题。

需要保持数据有序性:
二叉平衡树能够维护数据的有序性,同时也具有较高的查找效率。这在需要保持数据有序性并进行快速查找的场景中非常适用,例如索引数据库、缓存系统等。

需要高效的范围查询:
由于二叉平衡树能够维护数据的有序性,因此可以很高效地进行范围查询,例如查找某个区间内的所有元素。这在一些需要范围查询的应用中很有用,如地理信息系统、网络路由表管理等。

不适用场景:

数据集合变化较小:
如果数据集合的变化(插入、删除)很少,使用普通的二叉搜索树可能更加简单高效,因为不需要维护平衡性。

内存使用要求苛刻:
二叉平衡树需要存储额外的平衡信息(如高度、平衡因子),会占用更多的内存。如果内存使用非常受限,可能需要选择其他更简单的数据结构。

对写操作要求极高:
由于需要进行平衡操作,二叉平衡树的写操作(插入和删除)会稍微慢于普通的二叉搜索树。如果对写操作的性能要求极高,可能需要考虑其他数据结构。

总的来说,二叉平衡树是一种非常实用的数据结构,在需要高效管理动态有序数据集合的场景中表现优秀。但在某些特定的应用需求中,可能需要根据具体情况来权衡选择适合的数据结构。

** 画图不易，求赞。有不理解的地方可以私信我，必回复！ **