LeetCode-144-102-剑指Ⅰoffer55-优快云博客

本文链接：https://blog.youkuaiyun.com/hd_cash/article/details/123651988

本文详细解析了LeetCode中三道关于树的题目：144号题前序遍历、102号题层序遍历和55号题求最大深度。通过递归和队列实现，阐述了如何高效地遍历二叉树并获取其深度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

LeetCode144：

题目描述：
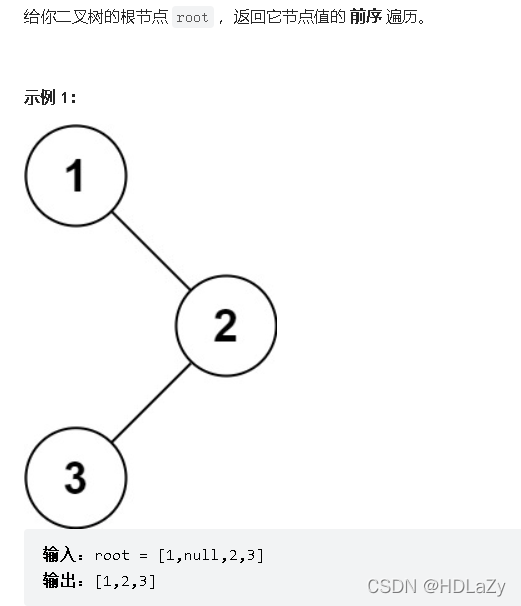
在这里插入图片描述

解题思路：
前序遍历，根节点->左子树->右子树
使用递归的思想，求当前树的前序遍历，则需要知道当前树的左子树和右子树的遍历顺序。
注意：该方法返回值是List，所有需要将节点的val存入list。

代码：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
        if(root==null){
            return list;
        }
        list.add(root.val);
        List<Integer> leftList=preorderTraversal(root.left);
        list.addAll(leftList);
        List<Integer> rightList=preorderTraversal(root.right);
        list.addAll(rightList);
        
        return list;
    }
}

LeetCode102：

题目描述：
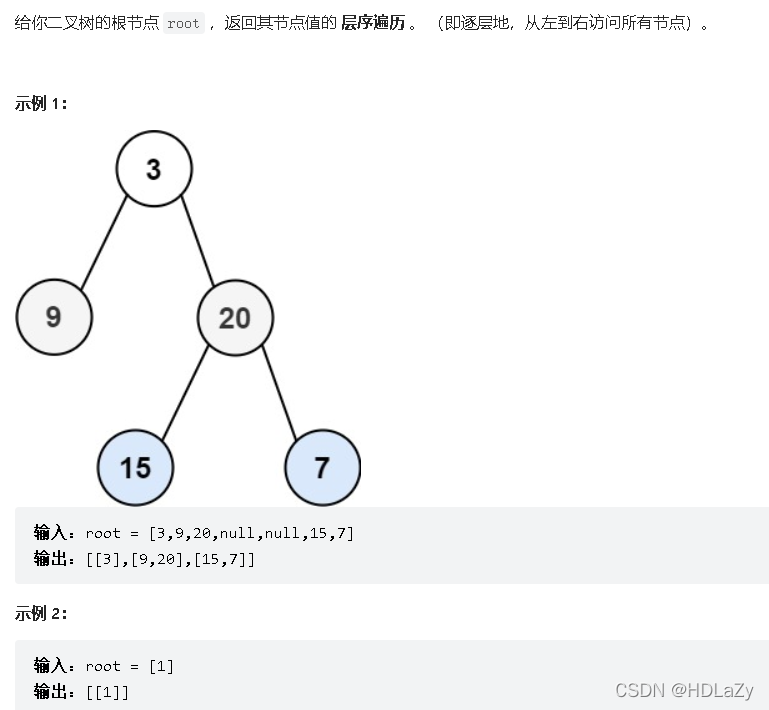
在这里插入图片描述
解题思路：
层序遍历，且该方法的返回值是List<List>，每一层的顺序就是一个List。
使用Queue队列来记录每一层的节点。当Queue不为空的时候，队首元素出队，并判断它是否存在左右子树，存在则将左右子树入队。如何确定队列中的元素是同一层？在遍历队列时，需要先记录队列的初始长度，每出队一个元素则减1，当size为0则表示一层结束。

代码：

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {

        List<List<Integer>> cur=new ArrayList<>();

        if(root==null){
            return cur;
        }

        Queue<TreeNode> queue=new LinkedList<>();
        queue.offer(root);


        while(!queue.isEmpty()){

            List<Integer> row=new ArrayList<>();
            int size=queue.size();
            while(size!=0){
            TreeNode r=queue.poll();
            row.add(r.val);
             if(r.left!=null){
                queue.offer(r.left);
            }
            if(r.right!=null){
                queue.offer(r.right);
            }
           
            size--;
            }
           
           cur.add(row);
            
        }

        return cur;

    }
}

offerⅠ55：

题目描述：
在这里插入图片描述

解题思路：
使用递归的思想，求当前树的深度，就是求当前树的max(左子树深度，右子树深度)+1。
代码：

class Solution {
    public int maxDepth(TreeNode root) {
            if(root==null){
                return 0;
            }
            int right=maxDepth(root.right);
            int left=maxDepth(root.left);
            return left>right? left+1:right+1;
    }
}