最优化之梯度下降(上升)算法
1、梯度下降算法原理
梯度下降(上升)法基于的思想是:要找到某函数的 最小(大)值,最好的方法是沿着该函数的梯度(反)方向探寻。如果梯度记为 ,则函数f(x,y)的梯度由 下式表示:
,则函数f(x,y)的梯度由 下式表示: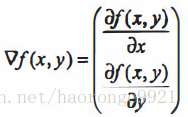 ,这是机器学习中最易造成混淆的一个地方,但在数学上并不难,需要做的只是牢记这些符号的意义。这个梯度意味着要沿x的方向移动
,这是机器学习中最易造成混淆的一个地方,但在数学上并不难,需要做的只是牢记这些符号的意义。这个梯度意味着要沿x的方向移动 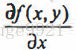 ,沿y的方向移动
,沿y的方向移动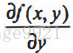 ,其中,函数’f(x,y)必须要在待计算的点上有定义并且可微。
,其中,函数’f(x,y)必须要在待计算的点上有定义并且可微。
梯度下降(上升)算法每次沿梯度(反)方向移动一步。梯度算子总是指向函数值减少(增加)最快的方向。这里所说的是移动方向,而未提到移动量的大小。该量值称为步长,记作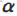 。用向量来表示的话,梯度算法的迭代公式如下:
。用向量来表示的话,梯度算法的迭代公式如下: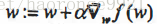 。该公式将一直被迭代执行,直至达到某个停止条件为止,比如迭代次数达到某个指定值或算法达到某个可以允许的误差范闱。
。该公式将一直被迭代执行,直至达到某个停止条件为止,比如迭代次数达到某个指定值或算法达到某个可以允许的误差范闱。
2、改进后的梯度下降算法–随机梯度下降算法
梯度上升算法在每次更新回归系数时都需要遍历整个数据集, 该方法在处理 100个左右的数据时还勉强可以接受。但如果有数十亿样本和成千上万的特征,那么该方法的计算复杂度就太高了。 一种改进方法是一次仅用一个样本点来更新回归系数,该方法称为随机梯度上升算法。由于可以在新样本到来时对分类器进行增量式更新,因而随机梯度上升算法是一个在线学习算法。
不过,随机梯度下降(上升)算法在多次迭代过程中回归系数的变化情况是不稳定的,有的系数只需要几十次迭代就能达到稳定值,有的系数则需要更多次的迭代。另外值得注意的是,有的系数在大的波动停止后,还有一些小的周期性波动。不难理解,产生这种现象的原因是存在一些不能正确分类的样本点(数据集并非线性可分),在每次迭代时会引发系数的剧烈改变。 我们期望算法能避免来回波动,从而收敛到某个值。另外,收敛速度也需要加快。
这就要考虑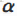 的大小,其值如果太小的话,那么下降的速度就会很慢; 如果太大的话,可能会错过最小(大)值,造成下降很不稳定,甚至会上升。因此, 应该选择合适的值,一种方法是在梯度较小的时候,选择小的,梯度较大的时候,选择大的,即正比于梯度
的大小,其值如果太小的话,那么下降的速度就会很慢; 如果太大的话,可能会错过最小(大)值,造成下降很不稳定,甚至会上升。因此, 应该选择合适的值,一种方法是在梯度较小的时候,选择小的,梯度较大的时候,选择大的,即正比于梯度算法.assets/1529915128805.png) 。这样保证了能够快速、稳定地得到最小(大)值。
。这样保证了能够快速、稳定地得到最小(大)值。




 本文介绍了梯度下降(上升)算法的基本原理和应用,包括如何沿着梯度(反)方向寻找最值点。同时,讨论了改进的随机梯度下降算法,它在大规模数据集和特征中具有较低的计算复杂度,是一种在线学习算法。然而,随机梯度下降算法的不稳定性以及选择合适步长的重要性是需要解决的问题。合适的步长应该与梯度大小成正比,以确保快速且稳定的收敛。
本文介绍了梯度下降(上升)算法的基本原理和应用,包括如何沿着梯度(反)方向寻找最值点。同时,讨论了改进的随机梯度下降算法,它在大规模数据集和特征中具有较低的计算复杂度,是一种在线学习算法。然而,随机梯度下降算法的不稳定性以及选择合适步长的重要性是需要解决的问题。合适的步长应该与梯度大小成正比,以确保快速且稳定的收敛。
















 2112
2112

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








