tensorflow课堂笔记（六）神经网络搭建的八股

"""
神经网络搭建的八股：
前向传播就是搭建网络，设计网络结构（forward.py）
def forward(x, regularizer):
    w=
    b=
    y=
    return y

def get_weight(shape, regularizer):
    w=tf.Variable()
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer(w))
    return w

def get_bias(shape):
    b=tf.Variable()
    return b

反向传播就是训练网络，优化网络参数（backwaor.py）
def backward():
    x=tf.placehlder()
    y_=tf.placeholder()
    y=forward.forward(x, REGULARIZER)
    global_step=tf.Variable(0, trainable=False)
    loss=

loss可以是：
y与y_的差距=tf.reduce_mean(tf.square(y-y_))
也可以是：
ce=tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
y与y_的差距（cem）=tf.reduce_mean(ce)
加入正则化后：
loss=y与y_的差距+tf.add_n(tf.get_collection('losses'))

指数衰减学习率
learning_rate=tf.train.exponential_decay(
    LEARNING_RATE_BASE,
    global_step,
    数据集总样本数/BATCH_SIZE,
    LEARNING_RATE_DECAY,
    staircase=True)
train_step=tf.train.GrandientDescentOptimizer(learning_rate).minimize(loss,global_step=global_step)

滑动平均
ema=tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY,gloabl_step)
ema_op=ema.apply(tf.trainable_variables())
with tf.control_dependencies([train_step, ema_op]):
    train_op=tf.no_op(name='train')

with tf.Session() as sess:
    init_op=tf.global_variable_initializer()
    sess.run(init_op)

    for i in range(STEPS):
        sess.run(train_step, feed_dict={x: ,y_: })
        if i % 轮数 == 0:
        print

if __name__ == '__main__':
    backward()
"""

generateds.py  生成数据集

#coding:utf-8
#0导入模块，生成模拟数据集
import numpy as np
import matplotlib.pyplot as plt
seed = 2
#param X 正态分布数据集 ， 2列
#param Y_ 根据X判断是否在圆中，是为1，不是为0
#param Y_c 将圆内点变成红色，圆外点变成蓝色
def generateds():
    #基于seed产生随机数
    rdm = np.random.RandomState(seed)
    #随机数返回300行2列的矩阵
    X = rdm.randn(300, 2)   #randn表示正态分布
    #取出每一行分析Y_的取值
    Y_ = [int(x0*x0 + x1*x1 < 2) for [x0, x1] in X]
    #在圆内的点为红色，圆外的点为蓝色
    Y_c = [['red' if y else 'blue'] for y in Y_]
    #对数据集X和标签Y进行形状整理，第一个维度根据第二个维度进行计算
    X = np.vstack(X).reshape(-1, 2)
    Y_ =np.vstack(Y_).reshape(-1, 1)   #Y_原来只有一行很多列，现在变成多行一列
    print(X)
    return X, Y_, Y_c

forward.py 前向传播

#coding:utf-8
#0导入模块，生成模拟数据集
import tensorflow as tf

#定义神经网络的输入，参数的输出，定义前向传播过程
def get_weight(shape, regularizer):
    w = tf.Variable(tf.random_normal(shape, dtype=tf.float32))#正态分布的变量
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w))
    return w

def get_bias(shape):
    b = tf.Variable(tf.constant(0.01, shape=shape))
    return b
#在这里设计了神经网络结构
#输出层-》隐藏层-》输出层，其中隐藏层有11个结点
def forward(x, regularizer):
    w1 = get_weight([2, 11], regularizer)   #2行11列的w，隐藏层有11个结点
    b1 = get_bias([11])                     #每一个w都要有一个偏置
    y1 = tf.nn.relu(tf.matmul(x, w1) + b1)  #得到1行11列向量

    w2 = get_weight([11, 1], regularizer)   #输出层的权重
    b2 = get_bias([1])                      #输出层偏置
    y = tf.matmul(y1, w2) + b2              #输出结果
    return y

backward.py 反向传播

#coding:utf-8
#0导入模块，生成模拟数据集
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import generagteds
import forward

STEPS = 40000
BATCH_SIZE = 30
LEARNING_RATE_BASE = 0.001  #初始的学习率
LEARNING_RATE_DECAY = 0.999 #指数衰减学习率中的衰减率
REGULARIZER = 0.01          #正则化参数
"""
指数衰减学习率
learning_rate = LEARNING_RATE_BASE*(LEARNING_RATE_DECAY)^\
                (global_step/decay_step),\
                其中 decay_step=sample_size/BATCH_SIZE
"""
def backward():
    x = tf.placeholder(tf.float32, shape=[None, 2])
    y_ = tf.placeholder(tf.float32, shape=[None, 1])
    X, Y_, Y_c = generagteds.generateds()
    y = forward.forward(x, REGULARIZER)    #前向传播后得到的结果
    global_step = tf.Variable(0, trainable=False)  #初始值为0且不可训练
    learning_rate = tf.train.exponential_decay(
        LEARNING_RATE_BASE,
        global_step,
        300/BATCH_SIZE,
        LEARNING_RATE_DECAY,
        staircase=True
    )

    #定义损失函数
    loss_mse = tf.reduce_mean(tf.square(y-y_))
    loss_total = loss_mse + tf.add_n(tf.get_collection('losses'))
    """
    tf.add_to_collection 向当前计算图中添加张量集合
    tf.get_collection 返回当前计算图中手动添加的张量集合
    tf.add_n 实现两个列表对应元素的相加
    """

    #定义反向传播方法：包含正则化
    train_step = tf.train.AdamOptimizer(learning_rate).minimize(loss_total)

    with tf.Session() as sess:
        init_op = tf.global_variables_initializer()
        sess.run(init_op)
        for i in range(STEPS):
            start = (i % BATCH_SIZE) % 300
            end = start + BATCH_SIZE
            sess.run(train_step, feed_dict={x: X[start:end], y_ : Y_[start:end]})
            if i % 2000 == 0:
                loss_v = sess.run(loss_total,feed_dict={x:X, y_:Y_})
                print("After %d steps, loss is : %f"%(i, loss_v))

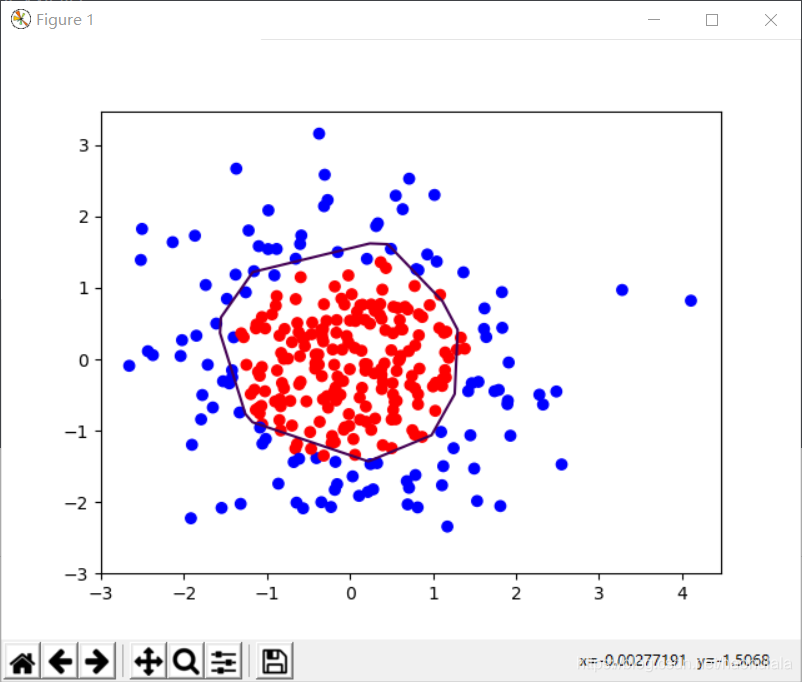
        xx, yy = np.mgrid[-3:3:.01, -3:3:.01]           #xx/yy.shape=(600,600)
        grid = np.c_[xx.ravel(), yy.ravel()]            #grid.shape=(360000,2)
        probs = sess.run(y, feed_dict={x:grid})         #y是前向传播得到的结果
        probs = probs.reshape(xx.shape)                 #probs.shape=(600,600)

    plt.scatter(X[:,0], X[:,1], c=np.squeeze(Y_c))      #scatter表示散点图，c表示color
    plt.contour(xx, yy, probs, levels=[.5])             #画出等高线(x,y,f(x,y),)
    plt.show()

if __name__=='__main__':
    backward()

输出结果：

After 0 steps, loss is : 22.403366
After 2000 steps, loss is : 0.388432
After 4000 steps, loss is : 0.220161
After 6000 steps, loss is : 0.178859
After 8000 steps, loss is : 0.149793
After 10000 steps, loss is : 0.135582
After 12000 steps, loss is : 0.128238
After 14000 steps, loss is : 0.122058
After 16000 steps, loss is : 0.121162
After 18000 steps, loss is : 0.121859
After 20000 steps, loss is : 0.117058
After 22000 steps, loss is : 0.116621
After 24000 steps, loss is : 0.118317
After 26000 steps, loss is : 0.115774
After 28000 steps, loss is : 0.115856
After 30000 steps, loss is : 0.117945
After 32000 steps, loss is : 0.115462
After 34000 steps, loss is : 0.115636
After 36000 steps, loss is : 0.117573
After 38000 steps, loss is : 0.115184