数学题库目录
说明
题目来源
本题库为三班网配套题库,本数学题库题目编号均为“M”开头。(答案在后面)
题目难度
难度分为以下七种,按从小到大排序:
入门 \colorbox{#FE4C61}{\color{white}\text{入门}} 入门、 普通- \colorbox{#F39C11}{\color{white}\text{普通-}} 普通-、 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-、 普通+/提高 \colorbox{#52C41A}{\color{white}\text{普通+/提高}} 普通+/提高、 提高+/困难- \colorbox{#3498DB}{\color{white}\text{提高+/困难-}} 提高+/困难-、 困难/地狱- \colorbox{#9D3DCF}{\color{white}\text{困难/地狱-}} 困难/地狱-、 困难+/地狱 \colorbox{#0E1D69}{\color{white}\text{困难+/地狱}} 困难+/地狱
另还有 暂未评定 \colorbox{#BFBFBF}{\color{white}\text{暂未评定}} 暂未评定难度
投题
本题库开放投题,投送题目可以获得一定的贡献值(暂未上线),需要提供对应的答案和解析(必须要有答案,如果没有解析获得的贡献值减半)
投题时可以给出难度,若不给,将会自动评定
题目不必须有名称
难度修改
难度为题目出现时设定。后续答对本题目者,可以对本题难度提供意见(微信私信发给我),综合评定后,会做出修改。
征集题解
没有题解的题目会开放征集题解,发送题解(微信私信发给我)并被选入,可以获得一定的贡献值。(可获得的贡献值会在题目解析处标出,题解被选入后会标注题解由谁提供。找出他人题解的错误并被核实后,也可以获得一定的贡献值)
题目
M0001 梦开始的地方
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:管理员添加
-
题目编号:M0001
-
题目名称:梦开始的地方
-
难度: 入门 \colorbox{#FE4C61}{\color{white}\text{入门}} 入门
-
题目类型:计算题
这是我们数学梦开始的地方。
你还记得你学数学时做过的第一个题吗?
没错,就是这道题。
在本题中,你只需要回答 1 + 1 1+1 1+1 的结果即可(正经题,禁止整活)。
M0002
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:管理员添加
-
题目编号:M0002
-
题目名称:–
-
难度: 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-
-
题目类型:选择题
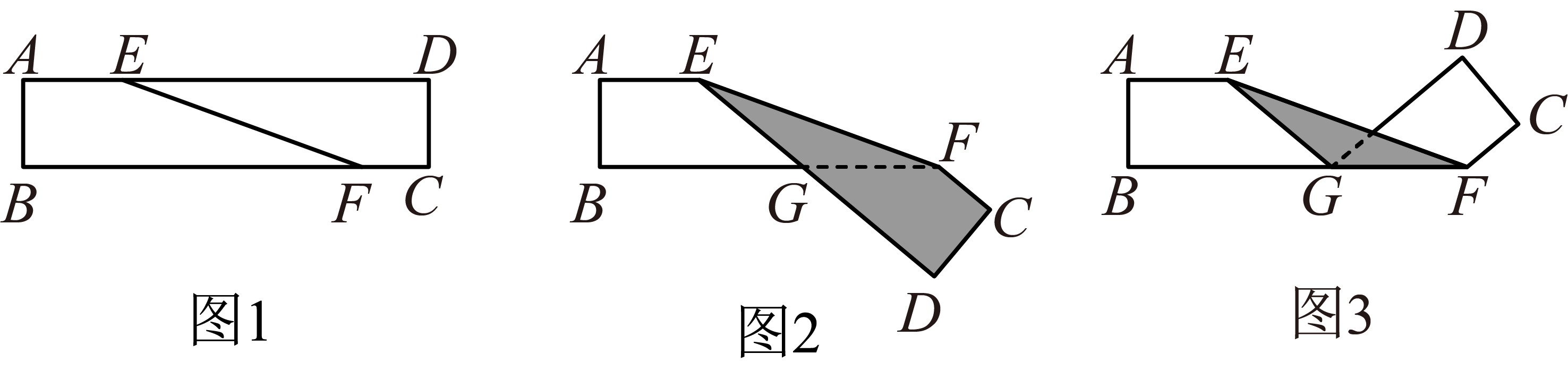
如图 1,四边形 A B C D ABCD ABCD 是长方形纸带,其中 A D ∥ B C AD\parallel BC AD∥BC, ∠ D E F = 20 ° \angle DEF=20\degree ∠DEF=20°,将纸带沿 E F EF EF 折叠成图 2,再沿 B F BF BF 折叠成图 3(在图 2 的基础上),则图 3 中 ∠ C F E \angle CFE ∠CFE 的度数是( )。
A. 110 ° 110\degree 110°
B. 120 ° 120\degree 120°
C. 140 ° 140\degree 140°
D. 150 ° 150\degree 150°
M0003
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0003
-
题目名称:–
-
难度: 普通- \colorbox{#F39C11}{\color{white}\text{普通-}} 普通-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T1
A 卷下载链接:2024 年暑假数学竞赛 A 卷试卷(需用电脑下载!!!)
以下四个坐标中,在第二象限的是
A. ( 3 , 2 ) (3,2) (3,2)
B. ( 3 , − 2 ) (3,-2) (3,−2)
C. ( − 3 , 2 ) (-3,2) (−3,2)
D. ( − 3 , − 2 ) (-3,-2) (−3,−2)
M0004
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0004
-
题目名称:–
-
难度: 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T2
已知关于 x x x 的不等式组 { 2 x + 10 < 20 5 x + m > 30 \begin{cases} 2x+10<20\\ 5x+m>30 \end{cases} {2x+10<205x+m>30 无解,则 m m m 的取值范围是
A. m < 5 m<5 m<5
B. m ≤ 5 m\le5 m≤5
C. m < 6 m<6 m<6
D. m ≤ 6 m\le6 m≤6
M0005
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0005
-
题目名称:–
-
难度: 普通- \colorbox{#F39C11}{\color{white}\text{普通-}} 普通-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T3
如图,直线 A B , C D AB,CD AB,CD 交于点 O O O,射线 O M OM OM 平分 ∠ A O C \angle AOC ∠AOC,若 ∠ B O D = 76 ° \angle BOD=76\degree ∠BOD=76°,则 ∠ B O M \angle BOM ∠BOM 是
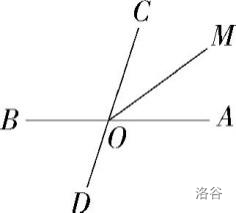
A. 38 ° 38\degree 38°
B. 104 ° 104\degree 104°
C. 142 ° 142\degree 142°
D. 144 ° 144\degree 144°
M0006
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0006
-
题目名称:–
-
难度: 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T4
如图, l ∥ A B l\parallel AB l∥AB, ∠ A = 2 ∠ B \angle A=2\angle B ∠A=2∠B。若 ∠ 1 = 108 ° \angle 1=108\degree ∠1=108°,则 ∠ 2 \angle 2 ∠2 的度数是
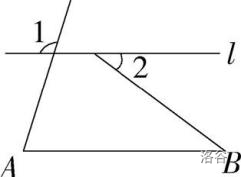
A. 36 ° 36\degree 36°
B. 46 ° 46\degree 46°
C. 72 ° 72\degree 72°
D. 82 ° 82\degree 82°
M0007
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0007
-
题目名称:–
-
难度: 普通+/提高 \colorbox{#52C41A}{\color{white}\text{普通+/提高}} 普通+/提高
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T5
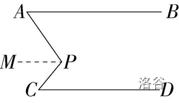
如图, A B ∥ C D AB\parallel CD AB∥CD,且 ∠ B A P = 60 ° − α \angle BAP=60\degree -α ∠BAP=60°−α, ∠ A P C = 50 ° + 2 α \angle APC=50\degree +2α ∠APC=50°+2α, ∠ P C D = 30 ° − α \angle PCD=30\degree -α ∠PCD=30°−α,则 α α α 是
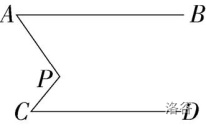
A. 10 ° 10\degree 10°
B. 15 ° 15\degree 15°
C. 20 ° 20\degree 20°
D. 25 ° 25\degree 25°
M0008
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0008
-
题目名称:–
-
难度: 普通- \colorbox{#F39C11}{\color{white}\text{普通-}} 普通-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T6
若 x + 3 x+3 x+3 是 16 16 16 的一个平方根,则 x x x 的值是
A. 1 1 1
B. − 7 -7 −7
C. 1 1 1 或 − 7 -7 −7
D. ± 7 \pm 7 ±7
M0009
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0009
-
题目名称:–
-
难度: 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T7
若关于 x x x 的等式 ( m − 4 ) x ∣ m − 3 ∣ = 26 (m-4)x^{|m-3|}=26 (m−4)x∣m−3∣=26 是一元一次方程,则 m m m 的值是
A. 4 4 4
B. 2 2 2
C. 4 4 4 或 − 2 -2 −2
D. ± 4 \pm 4 ±4
M0010
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0010
-
题目名称:–
-
难度: 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T8
下列说法中,正确的个数是
①点 A ( − a 2 − 1 , ∣ b ∣ + 1 ) A(-a^{2}-1,|b|+1) A(−a2−1,∣b∣+1) 一定在第二象限内
②点 P ( − 2 , 3 ) P(-2,3) P(−2,3) 到 y y y 轴的距离为 3 3 3
③若 P ( x , y ) P(x,y) P(x,y) 中 x = 0 x=0 x=0,则点 P P P 在 y y y 轴上
④若 x y = 0 xy=0 xy=0,则点 P ( x , y ) P(x,y) P(x,y) 一定在第二、四象限的角平分线上
A. 1 1 1
B. 2 2 2
C. 3 3 3
D. 4 4 4
答案及解析
M0001 梦开始的地方
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:管理员添加
-
题目编号:M0001
-
题目名称:梦开始的地方
-
难度: 入门 \colorbox{#FE4C61}{\color{white}\text{入门}} 入门
-
题目类型:计算题
-
涉及内容:简单计算
-
人教版衔接教材:一年级上册
答案: 2 2 2。
解析:简单计算即可。
M0002
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:管理员添加
-
题目编号:M0002
-
题目名称:–
-
难度: 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-
-
题目类型:选择题
-
涉及内容:折叠问题、平行线的性质
-
人教版衔接教材:八年级上册 第十三章
答案:B。
解析:在图 1 中, ∵ A D ∥ B C \because AD\parallel BC ∵AD∥BC,
∴ ∠ D E F = ∠ E F B = 20 ° \therefore \angle DEF=\angle EFB=20\degree ∴∠DEF=∠EFB=20°,
在图 2 中, ∠ G F C = 180 ° − 2 ∠ E F G = 140 ° \angle GFC=180\degree -2\angle EFG=140\degree ∠GFC=180°−2∠EFG=140°,
在图 3 中, ∠ C F E = ∠ G F C − ∠ E F G = 120 ° \angle CFE=\angle GFC-\angle EFG=120\degree ∠CFE=∠GFC−∠EFG=120°,
故选:B.
M0003
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0003
-
题目名称:–
-
难度: 普通- \colorbox{#F39C11}{\color{white}\text{普通-}} 普通-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T1
-
涉及内容:平面直角坐标系上象限的区分
-
人教版衔接教材:七年级下册 第七章
答案:C。
解析:根据平面直角坐标系上各个象限的坐标的正负性可得。
M0004
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0004
-
题目名称:–
-
难度: 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T2
-
涉及内容:一元一次不等式中未知数的求解
-
人教版衔接教材:七年级下册 第九章
答案:B。
解析:原式 = { 2 x + 10 < 20 ① 5 x + m > 30 ② =\begin{cases} 2x+10<20&①\\ 5x+m>30&② \end{cases} ={2x+10<205x+m>30①②,
解出 ① ① ① 式可得 x < 5 x<5 x<5,若要使不等式组无解,需要使不等式 ② ② ② 的解 x > a x>a x>a 中 a ≥ 5 a\ge5 a≥5,则设 x = 5 x=5 x=5,代入到 5 x + m = 30 5x+m=30 5x+m=30 中可得 m = 5 m=5 m=5 ,故 m ≤ 5 m\le5 m≤5.
故选:B。
M0005
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0005
-
题目名称:–
-
难度: 普通- \colorbox{#F39C11}{\color{white}\text{普通-}} 普通-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T3
-
涉及内容:邻补角与对顶角、角平分线的性质
-
人教版衔接教材:七年级下册 第五章
答案:C。
解析: ∵ ∠ B O C + ∠ B O D = 180 ° \because \angle BOC+\angle BOD=180\degree ∵∠BOC+∠BOD=180°
∴ ∠ B O C = 180 ° − ∠ B O D = 180 ° − 76 ° = 104 ° \therefore \angle BOC=180\degree-\angle BOD=180\degree-76\degree=104\degree ∴∠BOC=180°−∠BOD=180°−76°=104°
∵ ∠ A O C = ∠ B O D \because \angle AOC=\angle BOD ∵∠AOC=∠BOD
∴ ∠ A O C = 76 ° \therefore \angle AOC=76\degree ∴∠AOC=76°
∵ O M 平分 ∠ A O C \because OM平分\angle AOC ∵OM平分∠AOC
∴ ∠ C O M = 1 2 ∠ A O C = 1 2 × 76 ° = 38 ° \therefore \angle COM=\dfrac{1}{2} \angle AOC=\dfrac{1}{2} \times 76\degree=38\degree ∴∠COM=21∠AOC=21×76°=38°
∴ ∠ B O M = ∠ B O C + ∠ C O M = 104 ° + 38 ° = 142 ° \therefore \angle BOM=\angle BOC+\angle COM=104\degree+38\degree=142\degree ∴∠BOM=∠BOC+∠COM=104°+38°=142°
故选:C.
M0006( 本题征集题解 \colorbox{green}{\color{white}{\texttt{本题征集题解}}} 本题征集题解)
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0006
-
题目名称:–
-
难度: 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T4
-
涉及内容:邻补角与对顶角、平行线的性质
-
人教版衔接教材:七年级下册 第五章
答案:A。
解析:本题征集题解!!!
提交本题题解并被选入可获得 6 6 6 点贡献值!
M0007
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0007
-
题目名称:–
-
难度: 普通+/提高 \colorbox{#52C41A}{\color{white}\text{普通+/提高}} 普通+/提高
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T5
-
涉及内容:平行线的性质、猪蹄模型
-
人教版衔接教材:七年级下册 第五章
答案:A。
解析:如图,过点 P P P 作 P M ∥ A B PM\parallel AB PM∥AB
∴ ∠ B A P = ∠ A P M \therefore \angle BAP=\angle APM ∴∠BAP=∠APM
∵ A B ∥ C D \because AB\parallel CD ∵AB∥CD
∴ P M ∥ C D \therefore PM\parallel CD ∴PM∥CD
∴ ∠ P C D = ∠ M P C \therefore \angle PCD=\angle MPC ∴∠PCD=∠MPC
∴ ∠ A P C = ∠ A P M + ∠ M P C = ∠ B A P + ∠ P C D = 60 ° − α + 30 ° − α = 90 ° − 2 α \therefore \angle APC=\angle APM+\angle MPC=\angle BAP+\angle PCD=60\degree -α+30\degree -α=90\degree -2α ∴∠APC=∠APM+∠MPC=∠BAP+∠PCD=60°−α+30°−α=90°−2α
∴ 50 ° + 2 α = 90 ° − 2 α \therefore 50\degree +2α=90\degree -2α ∴50°+2α=90°−2α
∴ α = 10 ° \therefore α=10\degree ∴α=10°
故选:A.
M0008
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0008
-
题目名称:–
-
难度: 普通- \colorbox{#F39C11}{\color{white}\text{普通-}} 普通-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T6
-
涉及内容:平方根
-
人教版衔接教材:七年级下册 第六章
答案:C。
解析: ∵ ± 16 = ± 4 \because \pm \sqrt{16}=\pm 4 ∵±16=±4
∴ x + 3 = ± 4 \therefore x+3=\pm 4 ∴x+3=±4
∴ x = 1 或 − 7 \therefore x=1或-7 ∴x=1或−7
故选:C.
M0009
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0009
-
题目名称:–
-
难度: 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T7
-
涉及内容:绝对值、一元一次方程
-
人教版衔接教材:七年级上册 第一章、第三章
答案:B。
解析: ∵ ( m − 4 ) x ∣ m − 3 ∣ = 26 \because (m-4)x^{|m-3|}=26 ∵(m−4)x∣m−3∣=26 是一元一次方程
∴ m − 4 ≠ 0 , ∣ m − 3 ∣ = 1 \therefore m-4 \neq 0,|m-3|=1 ∴m−4=0,∣m−3∣=1
∴ m ≠ 4 , m = 4 \therefore m \neq 4,m=4 ∴m=4,m=4 或 2 2 2
∴ m = 2 \therefore m=2 ∴m=2
故选:B.
M0010
题目信息 {\color {blue} \texttt {题目信息}} 题目信息
-
题目提供者:郝国瑞
-
题目编号:M0010
-
题目名称:–
-
难度: 普通/提高- \colorbox{#FFC116}{\color{white}\text{普通/提高-}} 普通/提高-
-
题目类型:选择题
-
来源:2024 年暑假数学竞赛 A 卷 T8
-
涉及内容:绝对值、平面直角坐标系
-
人教版衔接教材:七年级下册 第七章
答案:B。
解析:①: ∵ a 2 ⩾ 0 \because a^2\geqslant 0 ∵a2⩾0
∴ − a 2 − 1 ⩽ − 1 \therefore -a^2-1\leqslant -1 ∴−a2−1⩽−1
∴ − a 2 − 1 < 0 \therefore -a^2-1<0 ∴−a2−1<0
∵ ∣ b ∣ ⩾ 0 \because |b|\geqslant 0 ∵∣b∣⩾0
∴ ∣ b ∣ + 1 ⩾ 1 \therefore |b|+1\geqslant 1 ∴∣b∣+1⩾1
∴ ∣ b ∣ + 1 > 0 \therefore |b|+1>0 ∴∣b∣+1>0
∴ \therefore ∴ 点 A ( − a 2 − 1 , ∣ b ∣ + 1 ) A(-a^{2}-1,|b|+1) A(−a2−1,∣b∣+1) 一定在第二象限内.
故 ① 正确.




















 19万+
19万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








