信号与系统【奥本海目】第二版笔记

最新推荐文章于 2024-03-02 20:12:21 发布

原创最新推荐文章于 2024-03-02 20:12:21 发布 · 2.7k 阅读

·

1

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

#信号与系统

专业专栏收录该内容

11 篇文章

订阅专栏

习题答案：https://mp.weixin.qq.com/s?__biz=MzU5OTYxODY1Mw==&mid=2247534141&idx=2&sn=81bee3f56a4d65da719543bdb5932879&chksm=feb0230fc9c7aa19612de53b02d618f0857ff1360dfcb905f66ffa4a37c76838b8d731bf88f1&token=1961583374&lang=zh_CN#rd

连续收敛级数
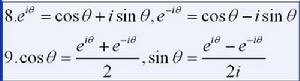
请添加图片描述

在这里插入图片描述 e^(ix)=cosx+isinx

第一章信号与系统

1.1 连续时间和离散时间信号

1 信号

信号：物质的运动形式或状态的变化。
表示：信号常用时间函数（或序列）表示。该函数的图像称为信号的波形。

在物理上，信号可以描述范围极广的一类物理现象。
在数学上，信号可以表示为一个或多个变量的函数。

连续时间信号
1.自变量是连续可变的，因此信号在自变量的连续值上都有定义
2.t表示连续时间变量
离散时间信号
1.自变量取在一组离散值上，也就是自变量仅取在一组离散值上
2.n表示离散时间变量

2 信号能量与功率

在这里插入图片描述
连续时间的总功率

1.2 自变量的变换

一。举例

1 时移

左加右减，变换后波形一致

2 时间变换

在这里插入图片描述

3 尺度变换

在这里插入图片描述

二。周期信号

1 周期信号

连续时间信号周期

一个周期连续时间信号x(t)具有这样的性质，即存在一个正值的T，对所有的t来说，有x(t)=x(t+T)

换句话说，当一个周期信号时移T后其值不变。这时就说x(t)是一个周期信号，周期为T。

1）、使上式成立的最小正值T成为x(t)的基波周期

2）、在x(t)为一个常数的情况下，基波周期无定义。

离散时间信号周期

如果一个离散时间信号x[n]时移一个N后其值不变，即对所有的n值有

x[n]=x[n+N]

则x[n]是周期的，周期为N，N为某一正整数。

2 非周期信号

一个信号x(t)不是周期的

三。偶信号与奇信号

1 偶信号

如果一个信号x(t)或x[n]，以原点为轴反转后不变，就称为偶信号。

连续时间信号：

x(-t)=x(t)

离散时间信号

x[-n]=x[n]

2 奇信号

如果一个信号x(t)或x[n]，以原点为轴反转后改变，就称为奇信号。

连续时间信号：

x(-t)=-x(t)

离散时间信号

x[-n]=-x[n]

3

任何信号都能分解为两个信号之后，其中一个为偶信号，另一个为奇信号
在这里插入图片描述

1.3 指数信号与正弦信号

一。连续时间复指数信号与正弦信号

1 连续时间复指数正弦信号

在这里插入图片描述

2 周期复指数和正弦信号

在这里插入图片描述
T0也叫基波周期

连续时间正弦信号或一个周期复指数信号，其基波周期T0是与|w0|成反比的，也称w0的基波频率

在这里插入图片描述

3 一般复指数信号

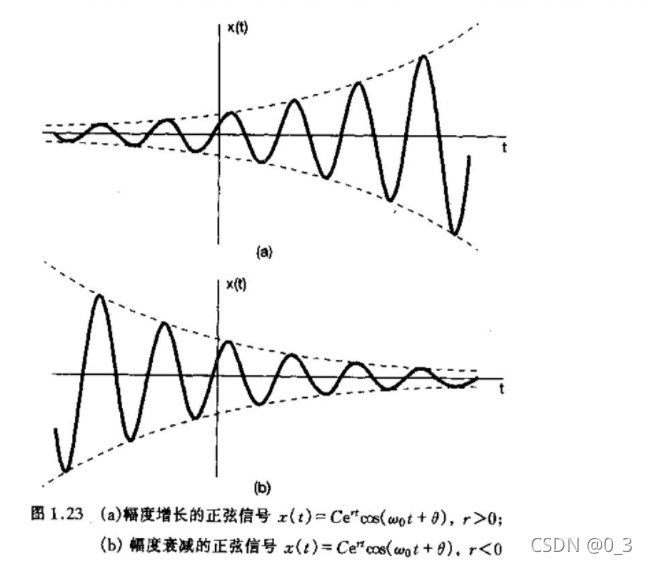
在这里插入图片描述

二。离散时间复指数信号与正弦信号

1 离散时间信号时复指数信号

与连续时间情况一样，一种重要的离散时间信号时复指数信号或序列，定义为在这里插入图片描述

2 实指数信号

如果C和a都是实数
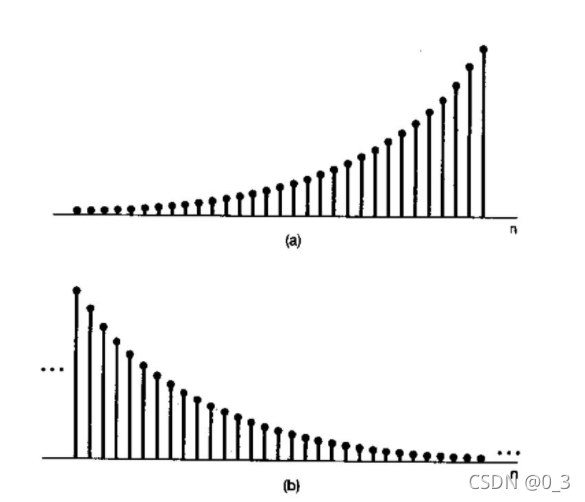
在这里插入图片描述

3 正弦信号

在这里插入图片描述
欧拉公式：

4 一般复指数信号

在这里插入图片描述

三。离散时间复指数序列的周期性质

在这里插入图片描述

1.4 单位冲激与单位阶跃函数

一。离散时间单位脉冲和单位阶跃序列

在这里插入图片描述

特性：

取样特性

解释：n=0才能取值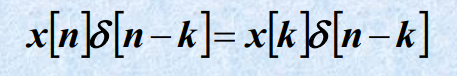
解释：n=k时才能取值
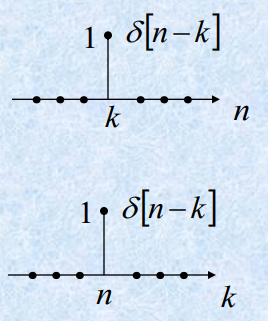
筛选特性

二。连续时间单位阶跃和单位冲激函数

在这里插入图片描述
36.。。。

1.5 连续时间和离散时间系统

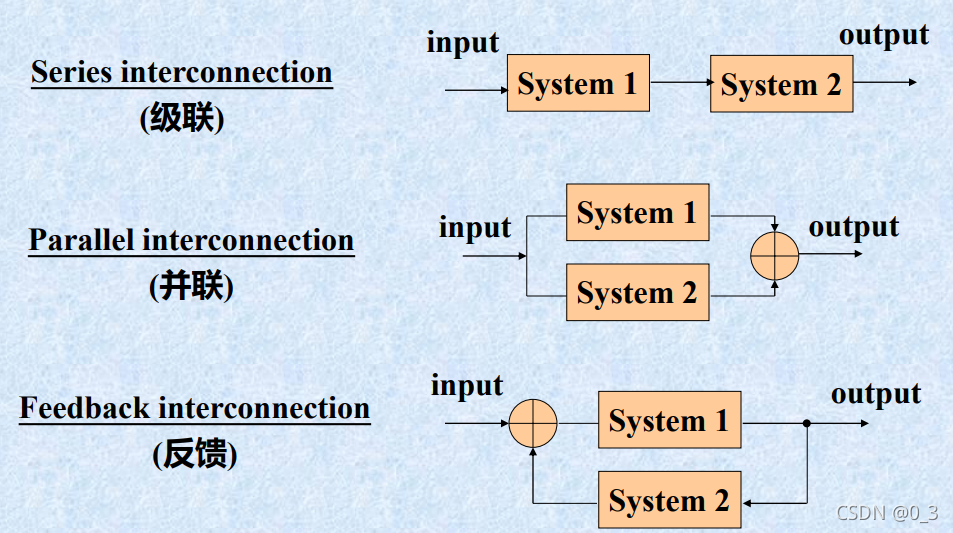
在这里插入图片描述

二。系统的互联

在这里插入图片描述

1.6 基本系统性质

一。记忆系统与无记忆系统

在这里插入图片描述

二。可逆系统与可逆性

在这里插入图片描述

三。因果性

在这里插入图片描述
无记忆系统都是因果的

四。稳定性

一个稳定系统在小的输入下的响应是不会发散。
在这里插入图片描述

五。时不变性

在这里插入图片描述

六。线性

在这里插入图片描述
课本p35

第二章线性时不变系统

2.1 离散时间线性时不变系统：卷积和

2.2 连续时间线性时不变系统：卷积积分

在这里插入图片描述

第三章周期信号的傅里叶级数表示

2 LTI系统对复指数信号的响应

在这里插入图片描述

H(s) 特征函数 e特征值

3 连续时间周期信号的傅里叶级数表示

一。连续时间傅里叶级数

11，
在这里插入图片描述

二。频谱的概念

15
在这里插入图片描述

三。傅里叶级数的其他形式

在这里插入图片描述
？

四连续时间傅里叶级数系数的确定

在这里插入图片描述
23

五。周期性矩形脉冲信号的频谱

在这里插入图片描述

4 连续时间傅里叶级数的收敛

在这里插入图片描述
狄拉克雷

5 连续时间傅里叶级数的性质

一。线性

在这里插入图片描述
p128 时移
23

六。共轭对称性

在这里插入图片描述

七。Parseval定理

在这里插入图片描述

6 离散时间周期信号的傅里叶级数表示

一。离散时间傅里叶级数（DFS）

在这里插入图片描述

二。傅里叶级数系数的确定

在这里插入图片描述

三。周期性方波序列的频谱

43？？

四。DFS的收敛

在这里插入图片描述

7 DFS的性质

在这里插入图片描述

8 傅里叶级数与LTI系统

在这里插入图片描述

第四章连续时间傅里叶变换

1 非周期信号的表示—连续时间傅立叶变换

一。从傅立叶级数到傅立叶变换

在这里插入图片描述

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。