开篇：预备知识-3

前言

我们在之前两篇文章中详细的介绍了一下 C语言的历史和关于 GCC 编译器的使用方法。这篇文章中我们来一起探讨一下关于信息数据在计算机是如何储存和表示的。有些小伙伴可能会问。数据就是储存在计算机的硬盘和主存中的啊。还能存去哪？确实，计算机中的所有数据都储存在有储存功能的部件中，这些部件包括内存、硬盘、CPU（寄存器）等。但是在这里我们要探讨的是数据在计算机中的表示形式，比如一个整型数 1 在计算机中的编码值，这是一个理论层面的东西，也可以理解为计算机科学家定制的一个标准。了解这些标准可以帮助我们更好的理解计算机的工作方式，写出更加健壮的程序。

信息表示的方法-编码

任何信息都是按照某个规则进行编码而得到的。我们日常见到的汉字、数字、英文等，当然也包括这篇文章。我们拿英语单词来举例子：

所有英语单词都是由 a~z 26 个字母中选取一个或者多个字母通过一定的顺序组合成的，这个过程就可以理解成编码：选取一个或者多个英文字母并按照一定顺序排列的过程。实际上，在这里我们把 英文字母 换成符号可能会更合适，因为从本质上来说，a~z 就是英语中 26 个用来进行信息表示的基本符号，至于为什么要采用 a~z 来作为基本符号，就得问这个语言的发明者了。

同样的，编码这个动作也适用于英语句子：所有的英语句子都是由一个或者多个英语单词按照一定的顺序组成的。

对于汉字也是一样的道理：中文中的一句话是由一个或者多个汉字组成的，而汉字又是由一个或者多个偏旁组成的。

对于不同层面的信息我们有不同的编码规则。但是只有经过了编码之后的符号才有意义。我们可以理解为：信息就是一个或者多个符号经过某个编码规则进行排列组合后得到的符号所表达的东西。

从古代的实物计数、结绳计数、筹码计数等到现代的罗马数字、阿拉伯数字，某个信息在不同的编码规则下可能有不同的符号表现。比如 ”五“ 这个数量词在罗马数字中用 V 符号表示，而在阿拉伯数字中用 5 这个符号来表示，但是它们表示的信息本质都是 五 这个数量词。

计算机中信息的编码

让我们的思绪回到现代社会。计算机帮我们 ”记住“ 和 ”做“ 了很多事情，这句话换一个描述方式是：计算机帮我们储存和处理了很多信息。而计算机内部采用 二进制 的形式来储存和处理信息。这意味着在计算机内部中，只有 0 和 1 两个符号可选。好在这两个符号数量是不受限制的。也就是说我们可以选取任意个 0 和 1 的符号进行排列组合，即编码，来得到无数个可能的结果（因为我们可以选取任意个 0 和 1）。通过这两个不同的符号已经足够描述这个世界了，只是在现实层面上我们缺少足够多的能够储存信息的介质而已，而这种介质在计算机中的最直接体现就是硬盘（无论再大，一个硬盘的容量也是有限的，容量大小时硬盘的物理属性之一）。

假设我们现在有 1 位的二进制数据，我们可以选取的二进制符号有 0 或者 1。这两我们通过排列组合得到的结果有两种可能：0、1。

如果可以选择 2 位的二进制数据呢？我们在第一位可以选择 0 或者 1，在第二位也可以选择 0 或者 1。这两我们通过排列组合得到的结果有 4 种可能性：00、01、10、11。

如果可以选择 n 位的二进制数据呢？我们通过排列组合得到的结果就有 2^n 种可能。

我们上面说过，将一个或者多个符号通过排列组合的过程就是编码。编码后的符号代表了某些信息。我们在上面已经通过二进制的符号（0 和 1）编码出了一些符号组合。但是并没有赋予其具体的含义。也就是说缺少了符号到信息的映射关系。这里的原因在于我们缺少一个实际场景，这里的缺少实际场景指的是我们还未指定这些符号要用来表示哪种类型的信息。我们来看看在计算机中这些符号组合分别代表什么信息。

信息的表示与处理

我们在上面已经知道了，编码出来的符号需要有实际的场景才可以表示对应的信息。而在计算机中这些符号表示的信息取决于这些符号被赋值给了哪种类型的变量。假设我们有一个编码出来的 8 位二进制符号：01000001，它代表的信息根据它的变量数据类型决定，我们拿 C语言中的数据类型举例子：

char

字符类型，每个变量占用 1 个字节（8位二进制）的储存空间。二进制符号范围为：00000000 ~ 11111111。一共可以有 256 个组合， 每一个值都被表示为了一个字符，对于上面的 01000001 来说。其表示的是大写字母 A，参见 [Ascii 字符对照表](#1、Ascii 码字符对照表)。我们可以通过代码验证：

#include <stdio.h>

int main() {
    // 0b 开头的代表这是一个二进制编码数据
  char c = 0b01000001;
  printf("%c\n", c);
  return 0;
} 

short

短整型类型，每个变量占用 2 个字节（16位二进制）的储存空间。二进制符号范围为 0000000000000000 ~ 1111111111111111。一共有 65536 种编码组合。 这种类型的每一种符号组合都被映射成了一个整数值。数值范围（10 进制为）：-32768 ~ 32767。至于为什么会是这个数值范围参考 整数的补码表示 小节。我们可以看到这个数值范围恰好把 short 类型的 65536 种组合用完了（-32768 ~ -1 一共 32768 用了种组合，0 ~ 32767 一共用了 32768，两个部分一共用了 65536 种组合）。

对于上面的 01000001 二进制编码符号来说，如果保存它的变量是 short 类型，那么其表示的含义是数字 65。我们可以通过代码验证：

#include <stdio.h>

int main() {
    // 0b 开头的代表这是一个二进制编码数据
  short c = 0b01000001;
  printf("%d\n", c);
  return 0;
} 

int

整型类型，在 64 位计算机上，每个变量占用 4 个字节（32位二进制）的储存空间，32 位计算机上（基本已经很少了），每个变量占用 2 个字节的储存空间（16 位二进制）。如果在 32 位机器上，这个类型就等价于 short 类型。我们这里只讨论 64 位计算机。其二进制符号范围为 00000000000000000000000000000000 ~ 11111111111111111111111111111111。一共有 4294967296 种编码组合。

和 short 类型类似，int 类型的每一个符号组合也被映射成了一个整数值。数值范围（10 进制为）：-2147483648 ~ 2147483647。所有数字的个数总和正好等于 4294967296，将 4294967296 种二进制编码的总和用完了。

和 short 类型 一样，对于上面的 01000001 二进制编码符号来说，如果保存它的变量是 int 类型，那么其表示的含义是数字 65。我们可以通过代码验证：

#include <stdio.h>

int main() {
    // 0b 开头的代表这是一个二进制编码数据
  int c = 0b01000001;
  printf("%d\n", c);
  return 0;
} 

long

长整型，每个变量占用 4 个字节（32位二进制）的储存空间。既然它是占用 4 个字节的储存空间，同时表示的信息又是整型数值类型，那么它的功能就和 int 一模一样（二进制符号范围一样、每个符号代表的信息也一样）。即可以理解为 long 类型是 int 类型的另一个别名。那么既然两个类型功能一样，还要新建一个重复功能但又名字不同的数据类型干嘛呢？我们这里讨论的类型占用储存空间的大小全部是针对 64 位机器而言的。而对于 32 位机器而言，int 类型变量占用的字节数为 2 个字节（16位二进制）。因此在早期（32位）计算机中，long 类型是为了描述 4 个字节的整型值而存在，而随着计算机的发展，到 64 位机器之后，int 类型的变量占用的字节数也变成了 4，因此这里 int 和 long 两种数据类型的功能就重合了。

long long

双长整型，每个变量占用 8 个字节（64位二进制）的储存空间，其二进制符号范围为 0000000000000000000000000000000000000000000000000000000000000000 ~ 1111111111111111111111111111111111111111111111111111111111111111。 一共有 1.8446744073709552e+19 种编码组合。

和 int 类型类似，long long 类型的每一个符号组合也被映射成了一个整数值。数值范围（10 进制为）：-9.223372036854776e+18 ~ 9.223372036854776e+18 - 1。所有数字的个数总和正好等于 1.8446744073709552e+19，将 1.8446744073709552e+19 种二进制编码的总和用完了。

和 int 类型 一样，对于上面的 01000001 二进制编码符号来说，如果保存它的变量是 long long 类型，那么其表示的含义是数字 65。我们可以通过代码验证：

#include <stdio.h>

int main() {
    // 0b 开头的代表这是一个二进制编码数据
  long long c = 0b01000001;
  printf("%d\n", c);
  return 0;
}

float

单精度浮点类型。每个变量占用 4 个字节（32 位二进制）的储存空间。二进制符号范围为：00000000000000000000000000000000 ~ 11111111111111111111111111111111 。你会发现和 int 类型的二进制符号范围一致，其实这个很好理解，因为都是用二进制来进行编码，占用的二进制位数（都是32）也一样，自然最后编码得到的符号范围和总数也一样。那么它们的区别在哪？其实就是对每个二进制编码出来的符号赋予的含义不同：在 int 类型中，每一个二进制符号都被表示成了一个整数，而在 float 类型中，每一个二进制符号都被表示成了一个浮点数。

对于上面的 01000001 二进制编码符号来说，如果保存它的变量是 float 类型，那么其表示的含义是一个小于 1 的浮点数。我们可以通过代码验证：

#include <stdio.h>

int main() {
    // 0b 开头的代表这是一个二进制编码数据
  int c = 0b01000001;
  float *cp = (float *)&c;
  // %.128f 表示输出一个浮点数，结果保留 128 位小数
  printf("%.128f\n", *cp);
  return 0;
} 

我们需要解释一下上面的代码：我们先将 01000001 二进制编码数据赋值给了一个 int 类型的变量 c。此时变量 c 在内存中的二进制编码表示为：00000000000000000000000001000001 。即（01000001）前面补齐了 24 个 0 位（int 类型占用 32 位二进制储存空间，当给定的二进制符号位数不足 32 位时，会在左边用 0 补齐剩下的位数）。然后，我们将 c 的地址强制转换成了 float 类型的指针，最后以 float 类型的编码解释模式输出了这个二进制编码数据代表的值。关于最后打印出来的结果为什么是截图上的小数值，可以参考 浮点数的表示 小节。

为什么不直接使用 float c = 0b01000001; 来给 float 类型变量赋值呢？因为如果这样写，那么这个数据就会先转换为 int 类型，也就是 10 进制的 65，然后再将 10进制的 65 这个值转换为对应的浮点数。而最终解码出来的值还是 65 这个数字。换句话来说 float c = 0b01000001; 写法和 float c = 65; 写法是没有区别的。采用这种写法时，这个 float 变量在计算机内容实际储存的二进制编码数据就不是 0b(24 个0)01000001 了。我们可以通过下面这段代码看一下当我们使用 float c = 0b01000001; 这种赋值方式时在内存中变量 c 的二进制编码数据：

#include <stdio.h>

/**
 * 打印出浮点数 f 在内存中的二进制编码数据 
 */
void showFloatBits(float f) {
  int *fp = (int *) &f;
  int size = sizeof(f) * 8;
  int i;
  for (i = 0; i < size; i++) {
    printf("%d", (*fp) >> (size - 1 - i) & 1);
  }
  printf("\n");
} 

int main() {
    // 0b 开头的代表这是一个二进制编码数据
  float c = 0b01000001;
  showFloatBits(c); 
  return 0;
} 

结果：

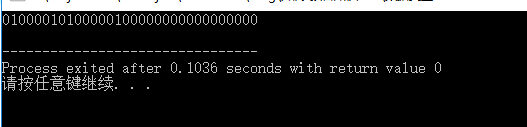
至于结果为什么是这个，可以参考 浮点数的表示 小节。

其实从上面的一系列代码实验我们已经可以看出：在计算机内存中储存的只是二进制符号数据，至于要将这个符号数据表示/“翻译” 成什么信息，那就取决于具体的场景，在这里这个场景就是储存这个二进制符号数据的变量类型。如果是字符类型数据（char），则按照 [Ascii 码字符对照表](#1、Ascii 码字符对照表) 来进行"翻译"。如果是整数类型（包括 short、int、long、long long 等），则按照 整数的表示规则 来进行翻译。如果是浮点数类型（float、double），则按照 浮点数的表示规则 来进行翻译。对于我们最开始的 01000001 这个二进制符号来说，如果保存这个二进制符号的变量是一个 char 类型变量，那么其表示的值为字母 A。如果保存这个二进制符号的变量是一个 short、int、long 类型的整型变量，那么其表示的是 10 进制数字 65。如果保存这个二进制符号的变量是一个单精度浮点数类型（float）的变量，那么其表示的是一个小数值：0.00000000000000000000000000000000000000000009108440018111311。如果是 double 类型的变量，其表示的小数将会更小，参见：double 小节。

只有绝对不变的符号，没有绝对不变的信息。

double

双精度浮点类型，每个类型占用 8 个字节的储存空间（64 位二进制）。和 float 类型类似，double 类型也是用来表示浮点数，不过每个 double 类型的变量占用 8 个字节的储存空间，在储存浮点数的范围和精度方面都有了很大的提升。因此其名为 双精度浮点类型。

对于上面的 01000001 二进制编码符号来说，如果保存它的变量是 double 类型，那么其表示的含义是一个小于 1 的浮点数。我们可以通过代码验证：

#include <stdio.h>

int main() {
    // 0b 开头的代表这是一个二进制编码数据
  long long c = 0b01000001;
  double *dp = (double *) &c;
  printf("%.1024lf\n", dp); 
  return 0;
} 

因为 double 类型变量占用 8 个字节的存储空间，所以这里先需要使用一个 long long 类型变量来承接初始的值（保证和 double 类型所占用的储存空间一致）。这里在内存中得到的二进制编码数据为：0000000000000000000000000000000000000000000000000000000001000001。即为在 01000001 前面补齐了 56 个 0 位，这一点和 int 类型类似，给定的二进制编码数据长度不满足数据类型所占用的位数，则会在左边补齐 0 。

后面其实和 float 小节的代码类似：将 long long 类型变量的指针强转为 double 类型的指针，然后将其在内存中实际储存的二进制编码翻译成 double 类型的浮点数。

double 类型能表示的浮点数精度比 float 大得多，因此这里为了能够展示出所有的非 0 小数，在打印时保留了 1024 位小数，从结果也可以看到对于同样的二进制编码：01000001，float 类型翻译出来的值和 double 类型翻译出来的值相差甚远。至于这个值为什么会是这个，请参考：浮点数的表示 小节。

到这里我们可以很清楚的知道：二进制编码符号只是做一个标识功能，至于这个符号要翻译成什么信息，取决于具体的数据类型是什么。

上面我们讨论的内存中二进制编码符号的翻译。这个规律类比到文件其实也是一样的。所有的文件本质上储存的都是二进制数据，这些二进制数据在被程序使用时要被 “翻译” 成什么样的信息就取决于文件类型，比如在 Windows 下 txt 类型的文件会被当成文本文件打开；png 类型的文件会被当成图片打开…。这就是我们上面的说的：信息的表示本质上是对二进制符号进行编码，具体的编码规则就取决于所处的场景，在编程语言中，其取决于保存二进制符号的数据类型；而在文件中，其取决于文件的后缀名（本质上还是取决于文件的解码方式，某种文件类型只是对应了一种解码方式）。

看到这里，相信你已经知道我们平时遇到的打开某些文本文件乱码的本质原因了。没错，就是因为解码文本文件中二进制符号的方式和保存这个文本文件时采用的编码方式不一致导致的。比如你采用 GBK 规则编码文本文件，却使用 ASCII 规则进行解码。这里的 GBK 和 ASCII 两种编码为两种不同的文本信息的表示方法，即为两种不同的编码规则。

整数的补码表示

我们已经在上面见过了 C语言中的表示整数的几种类型（short、int、long、long long）。我们在上面已经知道它们除了占用的内存空间不一样之外，采用的编码规则是一样的：都是采用二进制补码表示整数。我们拿 int 类型来举例，int 类型的二进制编码范围是：00000000000000000000000000000000 ~ 11111111111111111111111111111111。一共 2^32 种编码方式。这里的 2^32 种编码方式可以表示 2^32 种信息，在这里就是 2^32 个数字。

符号数

因为 int 类型的整数有负数的概念，因此我们将编码的第一位看成符号位，不计入值运算：0 代表正数、1 代表负数。

这样一分我们就相当于将这 2^32 中编码方式一分为二，第一部分为：10000000000000000000000000000000 ~ 11111111111111111111111111111111 ；第二部分为：00000000000000000000000000000000 ~ 01111111111111111111111111111111。第一部分我们用来表示负数，第二部分我们用来表示正数。这样表示之后我们会发现整数 0 有两个二进制符号表示：10000000000000000000000000000000 和 00000000000000000000000000000000。分别代表 -0 和 +0。但是这在数学上并没有意义，数学上数字 0 就是数字 0，没有正负之分。因此我们只让 00000000000000000000000000000000 这个二进制符号表示数字 0，将 10000000000000000000000000000000 这个二进制符号解放出来，让它表示 int 类型的最小值（即为负数中绝对值最大的数），这个值为 -2^31。

对于非负数（上文中的第二部分）。从小到大，我们用 00000000000000000000000000000000 （即32位全0的编码方式表示整数0），则整数 1 则为 00000000000000000000000000000001，整数 2 则为 00000000000000000000000000000010…如果按这种表示方式继续，整数的最大值则为 2^31-1，二进制符号为：01111111111111111111111111111111。这是正数部分的规律。

对于负数（上文中的第一部分），从小到大，我们从 10000000000000000000000000000000 开始，这个二进制编码符号代表是 int 类型的最小值：-2^31。而值 (-2^31) + 1 的二进制编码符号为 10000000000000000000000000000001（即为在最小值的基础上 + 1）。值 (-2^31) + 2 的二进制编码符号为 10000000000000000000000000000010， (-2^31) + 3 的二进制编码符号为 10000000000000000000000000000011…到最后，负数的部分的最大值为 -1。对应的二进制编码符号为 11111111111111111111111111111111。如果在这个基础上再加 1 的话，就发生溢出了，留下的 32 位二进制符号值为 00000000000000000000000000000000 ，变成了非负数的最小值，即为数字 0，再继续往上加的话就变成正数了。同样的，如果在正数的最大值 01111111111111111111111111111111 的基础上再加 1 的话，最高位的0 进位为了 1 ，二进制编码符号为：10000000000000000000000000000000 ，就变成了负数的最小值。从这里我们可以看出：正数的最大值和负数的最小值在二进制编码符号上是相邻的，正数的最小值和负数的最大值在二进制编码符号上也是相邻的，我们可以用一幅图来表述这个规律：

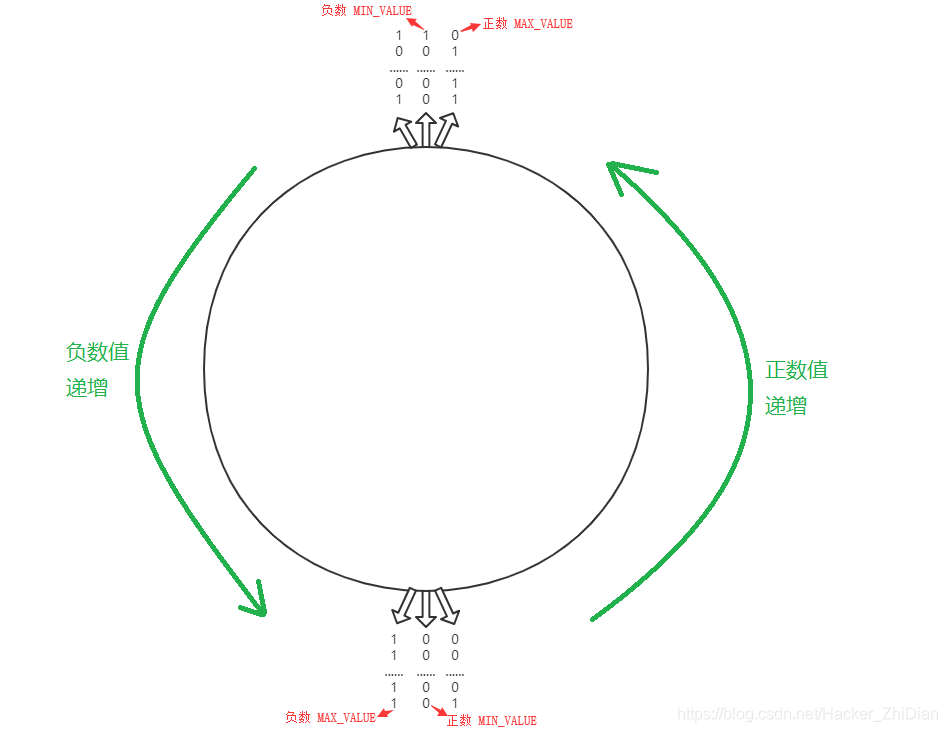
图中的整个圆形代表了 32 位二进制符号可以表示的所有符号总数，在几个特殊的位置，标注了这个二进制符号对应的 int 类型特殊值。同时通过箭头表明了符号改变的规律对应着 int 的变化规律。我们可以发现整个圆形的值随着逆时针方向，对应的 int 值是递增的，到达了南北两个极点之后，值发生对调（负数最大值->正数最小值，正数最大值->负数最小值）。于是整个部分形成了一个环，理解这个规律很重要，我们在 溢出 小节还会讨论到这个问题。

我们在上面讨论的这种整数的表示方式称为 整数的补码表示，对应的，还有整数的原码、反码表示方式，但是由于补码可以使得计算机可以以加法的形式来进行减法，因此最终计算机科学家们将二进制补码作为有符号整数最终的表示方式。

无符号数

我们在上文讨论了 int 类型（带符号数）的二进制编码表示。对于无符号数（unsigned int）类型就更简单了，因为是无符号数，所以所有的二进制编码符号都是用来表示非负整数。对于 unsigned int 来说，其共有 2^32 中二进制编码符号，因此可以表示的整数的范围为： 0 ~ 2^32-1 。这部分规律可以用如下图来表示：

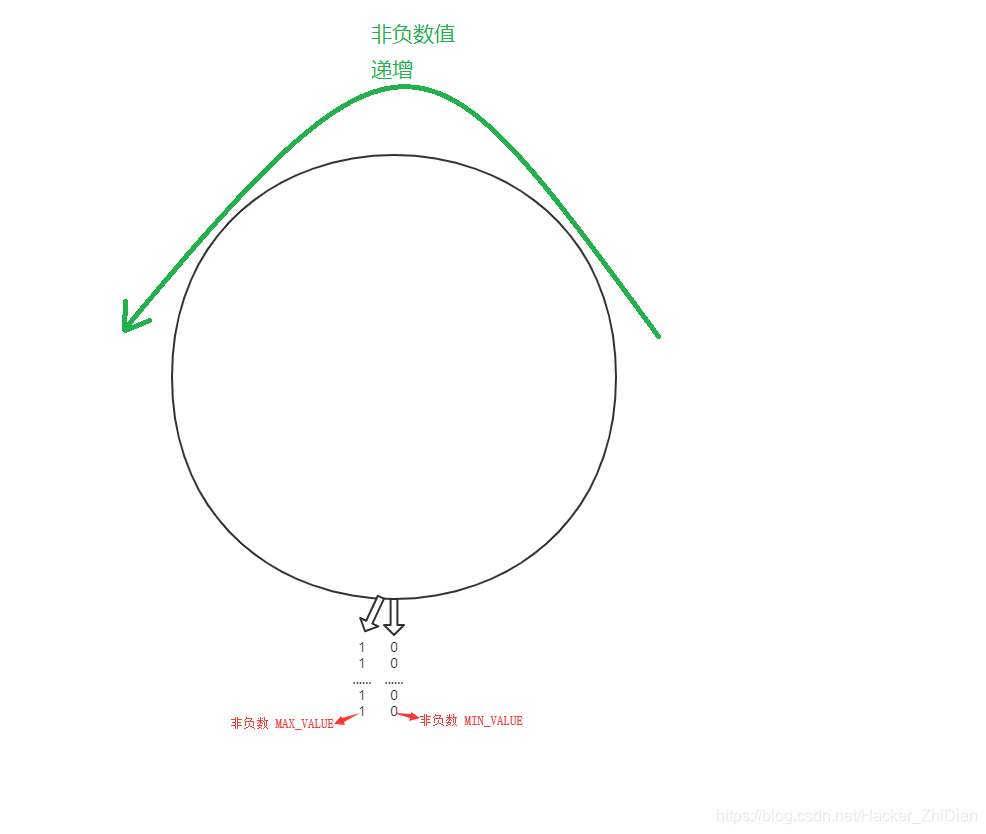
对于无符号数来说，只有两个极点值：非负数的最大值和非负数的最小值，并且这两个极点值是相邻的。在这个圆中，和上面的图一样，依然有 2^32 种二进制符号的编码方式，但是因为我们解释这些符号的规则不一样了（这里不需要将最高位当成符号位来解释了）。因此在这里对于某些（最高位为 1 的）二进制编码符号来说，得到的数值和上面相同的二进制编码符号不一样。

浮点数的表示

C语言中提供了两种浮点数类型（float、double），分别对应于单精度浮点和双精度浮点数。它们占用的内存字节数分别为 4 个字节和 8 个字节。既然规定了占用的字节数，那么这两种类型的二进制编码数目也就确定了。分别是 2^32 种和 2^64 种。我们分别来看一下这两种数据类型对于二进制编码的解释方式：

单精度浮点

单精度浮点类型把 4 个字节， 32 位 Bit 储存空间划分为如下部分：

双精度浮点

双精度浮点类型把 8 个字节，64 位 Bit 储存空间划分为如下部分：

两种浮点类型的区别在于占用的储存空间不同，因此能表示的浮点数的范围和精度也不一样。但是解释二进制编码的规则是一样的：

浮点数的解释规范

不管是单精度浮点数还是双精度浮点数，都是将对应的内存 Bit 位分成了 3 个部分：s、exp 和 frac。

1、s(sign) : 符号位，和整数类型类似，浮点数也要有正负标识，这就是我们熟知的符号位，占用一个 bit 位，值为 0 代表正数、1 代表负数。

2、exp(exponent): 阶码，这个值会被解释成一个无符号整数，我们先标记为 e；

3、frac: 尾数，这个值会被解释成一个二进制小数，我们先标记为 f。

浮点数最终的值解释公式为：V = (-1)^s * M * 2^E。

其中 M 和上面的尾数部分（frac）相关联， E 和上面的阶码部分（exp）相关联，根据 exp 部分的值，最终得到的值会有三种解释方式，这三种解释下 M 和 E 的值又不尽相同，我们来看一下：

1). 规格化的值

当浮点数中 exp 部分的值不全为 0(00000000) 并且不为 1(11111111)。会采用该方式来对浮点数进行解释。此时上面浮点数解释公式中的 M 值公式为 M = 1 + f。f 即为上面的尾数部分解释成了二进制小数后的值。 E 的值公式为 E = e - Bias。其中 Bias 是一个常量值，在单精度浮点中为 127（2^(7) - 1）。在双精度浮点中为 1023（2^(10) - 1）。Bias 值的规律为 2^(阶码的位数-1) - 1 。

浮点数中绝大多数值都是规范化的值，我们来举个例子，假设在计算机内存中有一个二进制编码为 00111111001100000000000000000000 的 float 类型浮点数，它的 10 进制值是多少呢？我们按照上面的浮点数 Bit 划分来分别取出 s、exp 和 frac 部分的数据

1、s: 左边第一位符号为 0，因此这个浮点数是一个正数。

2、exp: 从左边第二位开始，向右数 8 位，值为 01111110，因此这是一个规范化的浮点数，得到的 E 值为 e - Bias = 126 - 127 = -1 。

3、frac: 从右边第一位开始，向左数 23 位，值为 01100000000000000000000。即为 0.01100000000000000000000。转换为小数值为 2^(-2) + 2^(-3) = 3/8。此时得到的 M 值为 1 + f = 11/8。

最后，根据浮点数的计算公式：V = (-1)^s + M * 2^E。得到的最终10 进制小数值为：(-1)^0 + 11/8 * 2^(-1) = 11/16。我们还是用计算机帮我们验证吧：

#include <math.h>
#include <stdio.h>

int main() {
  int i = 0b00111111001100000000000000000000;
  float *p = &i;
  printf("%f\n", *p);
  printf("%f", 11/16.0f);
  return 0;
}

结果：

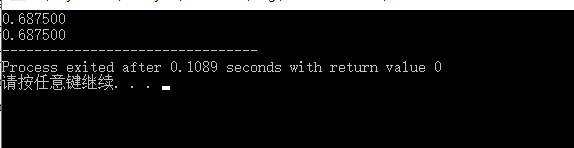
可以看到 11/16.0f 的值和我们手动解析 float 类型的二进制编码得到的值相同。

2). 非规格化的值

当浮点数中 exp 部分的值全为 0(00000000) 时，代表该浮点数是非规范化的。会采用该方式对浮点数进行解释。此时上面浮点数解释公式中的 M 值公式为 M = f。f 即为上面的尾数部分解释成了二进制小数后的值。E 值公式为 E = 1 - Bias，Bias 和上面规格化的规则一样，单精度浮点中值为 127。双精度浮点值为 1023。

浮点数中也有很大一部分数值是非规范化的， 我们拿 float 小节中遗留的数据，类型为 float，值为 00000000000000000000000001000001 的单精度浮点数据来举例

1、s: 左边第一位符号位为 0，因此这个浮点数是一个正数。

2、exp: 从左边第二位开始，向右数 8 位，都是 0，因此这是一个非规范化的浮点数，得到的 E 值为 1 - Bias = -126。

3、frac: 从右边第一位开始，往左边数 23 位，值为 00000000000000001000001，实际值即为 0.00000000000000001000001。转换为 10 进制小数为：M * 2^E = (2^(-17) + 2^(-23)) * 2^(-126) = ...

最后，根据浮点数的计算公式：V = (-1)^s + M * 2^E。得到的最终10 进制小数值为：(-1)^0 + M * 2^(-126)。因为数字过于复杂，我们还是用计算机帮我们验证吧：

#include <math.h>
#include <stdio.h>

int main() {
  float a = (float) ((pow(2, -17) + pow(2, -23)) * pow(2, -126));
  printf("%.128f\n", a);
  return 0;
}

结果：

这个结果和 float 小节中得到的运算结果是一致的！

3). 特殊值

当浮点数中 exp 部分的值全为 1(11111111) 时。此时的值有以下 2 种情况：

[1]. 小数部分(frac)全为 0 时，得到的值表示无穷，此时 s 为 0 时表示正无穷，为 1 表示负无穷。当我们把两个非常大的浮点数相乘，或者除以 0.0f 时，会得到这个值。

[2]. 小数部分(frac) 不全为 0 时，得到的称为 NaN（not a numer），即 “不是一个数字”。NaN 和任何数运算结果都是 NaN。

浮点数的范围

单精度浮点数(float)

从上面规律可以知道，对于单精度浮点数来说（float）类型，其能表示数据的最小值对应的二进制编码为：11111111011111111111111111111111。此时的 s、exp、frac 的值分别为：

s: 1。意味着这是一个负数。

exp: 11111110，既不为全 0 也不为全 1，意味着这是一个规格化的浮点数，e = 254。

frac: 11111111111111111111111，即为 0.11111111111111111111111 = 1 - 1/(2^(23))，f = 1 - 1/(2^(23))。

此时对应的 E 为：e - Bias = 254 - 127 = 127。M 为：M = 1 + f = 2 - 1/(2^(23))。此时得到的浮点数值为：V = -1^(s) * M * 2^E = -3.4028234663852886e+38。负数最小值是这个，那么对应的正数最大值自然是将 s 符号位值改为 0 的时候了，对应的正数最大值为3.4028234663852886e+38。

因此单精度浮点数(float) 能表达的数字范围为：-3.4028234663852886e+38 ~ 3.4028234663852886e+38。

双精度浮点数(double)

对于双精度浮点数来说（double）类型，其能表示数据的最小值对应的二进制编码为：1111111111101111111111111111111111111111111111111111111111111111。此时的 s、exp、frac 的值分别为：

s: 1。意味着这是一个负数。

exp: 11111111110，既不为全 0 也不为全 1，意味着这是一个规格化的浮点数，e = 2046。

frac: 1111111111111111111111111111111111111111111111111111，即为 0.1111111111111111111111111111111111111111111111111111 = 1 - 1/(2^(52))，f = 1 - 1/(2^(52))。

此时对应的 E 为：e - Bias = 2046- 1023 = 1023。M 为：M = 1 + f = 2 - 1/(2^(52))。此时得到的浮点数值为：V = -1^(s) * M * 2^E = -1.7976931348623157e+308。负数最小值是这个，那么对应的正数最大值自然是将 s 符号位值改为 0 的时候了，对应的正数最大值为 1.7976931348623157e+308。

因此双精度浮点数(double) 能表达的数字范围为：-1.7976931348623157e+308 ~ 1.7976931348623157e+308。

不精确的浮点数

在数学中，0 ~ 1 之间的小数可以有无限多个，因为我并没有限制小数的位数。但是在计算机中就不存在 “无限多个” 这种说法，就如同计算机的储存介质是有限的一样。不管我们用 32 位的浮点数（float）还是 64 位的浮点数（double），因为它们的二进制编码总数是有限的。那么它们能表示的浮点数的个数总就是有限的。因此对于某些特殊的小数，在计算机中就会出现没办法精确表示的情况。

举个例子，假设我们要用一个 float 类型的变量保存 10 进制的浮点数 0.1。我们很容易就可以写出这段代码：

#include <math.h>
#include <stdio.h>

int main() {
  float a = 0.1f;
  return 0;
}

但是如果此时你把 a 打印出来：

#include <math.h>
#include <stdio.h>

int main() {
  float a = 0.1f;
    // 保留小数点后面 32 位小数
  printf("%.32f\n", a);
  return 0;
}

结果：

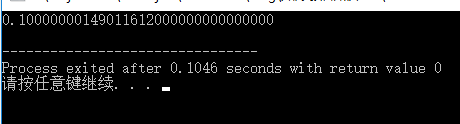
很奇怪对不对，赋值进去的明明是 0.1，怎么打印出来的结果是略微比 0.1 大一点的值呢，我们不妨看一下变量 a 中在内存的二进制编码：

#include <stdio.h>

/**
 * 打印出浮点数 f 在内存中的二进制编码数据 
 */
void showFloatBits(float f) {
  int *fp = (int *) &f;
  int size = sizeof(f) * 8;
  int i;
  for (i = 0; i < size; i++) {
    printf("%d", (*fp) >> (size - 1 - i) & 1);
  }
  printf("\n");
} 

int main() {
  float c = 0.1f;
  showFloatBits(c); 
  return 0;
} 

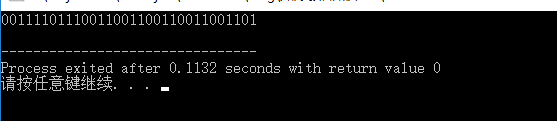
得到的结果为：00111101110011001100110011001101，我们将这个二进制编码按照浮点数解释规范来拆分，到的值如下

s: 0.

exp: 01111011 = 123.

frac: 10011001100110011001101 = 0.10011001100110011001101 = 2^(-1) +2^(-4) + 2^(-5) + 2^(-8) + 2^(-9) + 2^(-12) + 2^(-13) + 2^(-16) + 2^(-17) + 2^(-20) + 2^(-21) + 2^(-23)。

根据 exp 的值，我们知道这是一个规范化的浮点数，因此

E= e - Bias = 123 - 127 = -4。

M = 1 + f。

最后得到：V = 2^(-4) * M。用计算机帮我们算：

#include <math.h>
#include <stdio.h>

int main() {
  float M = (float) (1 + pow(2, -1) + pow(2, -4) + 
    pow(2, -5) + pow(2, -8) + pow(2, -9) + pow(2, -12) + pow(2, -13) + 
    pow(2, -16) + pow(2, -17) + pow(2, -20) + pow(2, -21) + pow(2, -23));
  float E = (float) pow(2, -4);
  
  float a = (float) (M * E);
  printf("%.32f\n", a);
  return 0;
}

结果：

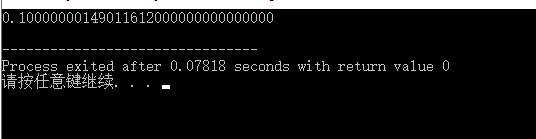
可以看到，和之前直接打印出 a 的结果一样。这说明浮点数编码规则是没错的，那为什么不精确呢？其实从上面的 a 的内存二进制编码打印结果中就可以知道了，frac 部分的值为 10011001100110011001101。 23 位表示小数部分的 bit 已经用完了，依然没有办法精确的表示所需要的小数。那么只能取这个值了（float 对 0.1 说：我最多只能表示到这个精度了，还是没有办法精确的表示你，那我也没办法了，我尽力了）。但是我们在打印的时候会按正常的浮点数解释规则对这个二进制编码进行解释，因此得到的浮点数就是不精确的。

这个问题我们可以通过提高浮点数的精度来改善，比如把 a 换成 double 类型的，这样就有 52 位 bit 可以用来表示小数部分了。但是这也仅仅是改善，不能解决这个问题，小伙伴们仔细观察一下就会知道：在数据类型为 float 时， 0.1 的 frac 部分是以 1001 的无限循环，这就和我们 10 进制中的无限循环小数一样。而在有限的计算机内存中，显然是无法精确表示的。我们还是用 double 类型来验证一下：

#include <math.h>
#include <stdio.h>

int main() {
  double a = 0.1;
  printf("%.128f\n", a);
  return 0;
}

结果：

确实有了很大改善，但还是偏大一点，我们再打印出此时的变量 a 在内存中而进制编码数据：

#include <stdio.h>

/**
 * 打印出浮点数 f 在内存中的二进制编码数据 
 */
void showFloatBits(double f) {
  int *fp = (int *) &f;
  int *fpNext = fp++;
  int size = sizeof(int) * 8;
  int i;
  // 打印前 4 字节数据 
  for (i = 0; i < size; i++) {
    printf("%d", ((*fp) >> (size - 1 - i)) & 1);
  }
  // 打印后 4 字节数据 
  for (i = 0; i < size; i++) {
    printf("%d", ((*fpNext) >> (size - 1 - i)) & 1);
  }
  printf("\n");
} 

int main() {
  double c = 0.1;
  showFloatBits(c); 
  return 0;
} 

结果：

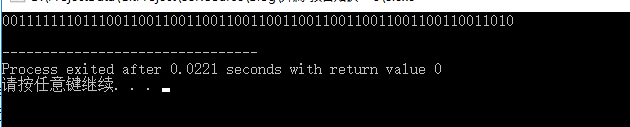
同样的，按照浮点数的解释规则进行分隔：

s: 0

exp: 01111111011

frac: 1001100110011001100110011001100110011001100110011010

这里我们不再重新计算浮点数据了，可以观察到，此时的 frac 还是以 1001 重复的无限循环，相对 float ，这个循环的位数提高了（从 23 到 52），这意味着值会更加精确，但是依然无法完全精确的表示 0.1 。如果对精度要求很高，需要使用高精度的浮点数类型，C语言中本身没有提供，需要自己实现，Java 中有 BigDecimal 类可供使用。

溢出

数学上没有溢出的概念，只有进位的概念，因为在数学上默认可用的数字空间是无限的，是一种理论模型。但是到了计算机上面就不是这样的了，我们拿两数相加来举例子，如果我要计算 10 进制数 516 + 728。我们会在草稿纸上写下如下步骤：

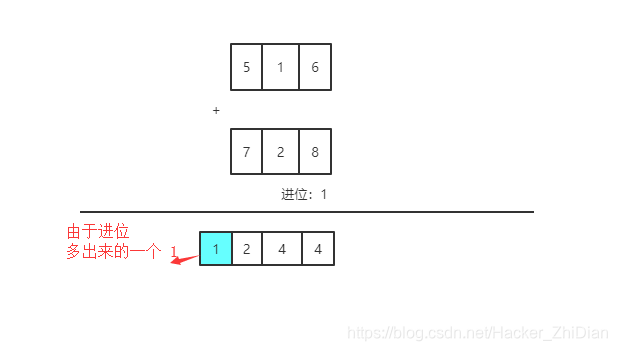
结果等于 1244。是一个四位数，而我们参与运算的两个数字都是三位数，也就是说我们如果要以 10 进制数储存 516 + 728 的运算结果的话需要 4 个单位的储存空间，这里说的单位指的是能储存数字 0~9 的硬件。

但是我们的计算机用的是存储 0~1 的硬件，所以只能储存二进制储存数据，如果我们要在计算机中模拟出上述计算过程，必须先将运算数转换成二进制数字：516 -> 1000000100。728 -> 1011011000。于是这个运算过程就变成了：

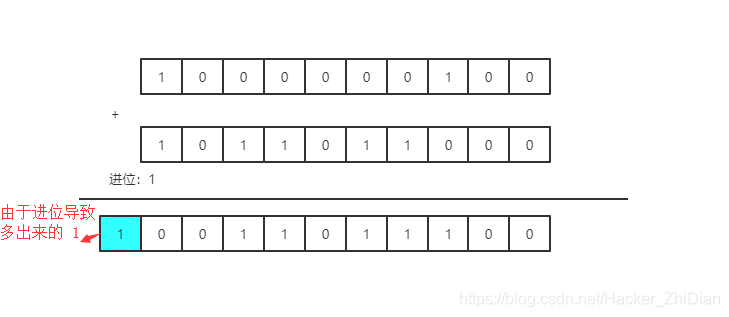
可以看到，两个运算数都是占用 10 位（bit）储存空间的数字，我们可以用 short 类型来保存着两个运算数（short 类型有用两个字节，16 bit 的存储空间，最左边的 1 位用来标识符号，有 15 位 bit 可以用来储存值）。运算结果占用 11 位（bit）的储存空间。这本是一个再正常不过的运算式，但是如果我们把两个运算数再扩大一点的话，情况可能就不是这样了，现在我们把算式改成：100000010000000 + 101101100000000，这个运算过程就变成了：

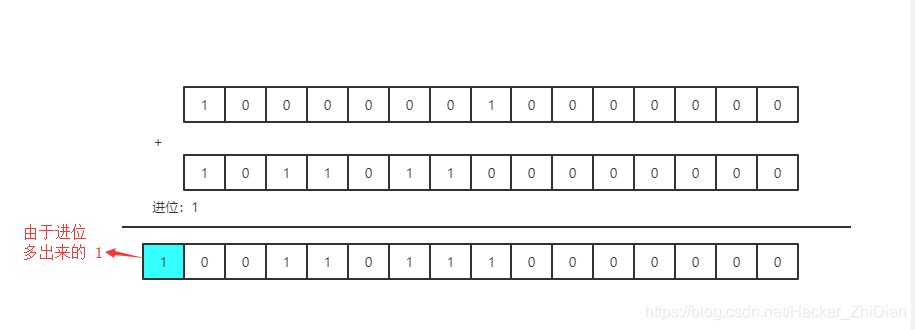
此时的出来的结果为 1001101110000000。如果用 short 类型保存这个数据的话，得到的值是：-25728。我们用代码来验证：

#include <stdio.h>

int main() {
  short valueA = 0b100000010000000;
  short valueB = 0b101101100000000;
  short s = valueA + valueB;
  printf("a = %d\n", valueA);
  printf("b = %d\n", valueB);
  printf("a + b = %d\n", s);
  return 0;
}

结果：

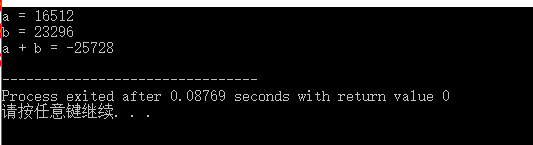
很显然，这个结果并不是我们想要的。为什么两个正数做加法得到的结果会是负数？其实答案已经在上面的二进制运算过程图中：我们的两个运算数相加得到的结果已经超过了 short 类型能表示的整数的最大值（65535），对应的二进制补码是 0111111111111111，而我们运算得到的结果是 1001101110000000 。很明显，运算过程中最左边的 0 由于进位被置为 1 ，而作为一个有符号整型，最左边的 1 位代表符号位。此时，根据有符号整数的补码表示规则。得到的值就是一个负数。具体的值为：-2^15 + 0 + 0 + 2^12 + 2^11 + 0 + 2^9 + 2^8 + 2^7 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = -25728。

其实上面的运算已经产生了溢出，运算的结果超过了该类型能表示的最大值。还记得我们在 符号数 小节中的那张圆形图吗？圆形左边的值代表负数，右边代表正数。如果你的运算结果超过了其数据类型能表示的正数的最大值，那么就会反转到圆形的左边，即变成负数。同样的，对于负数运算也是如此。

对于上面的问题，我们有很多种解决方法，这里举两种：

1、将 valueA、valueB、s 的类型变成 unsigned short，即变成无符号短整类型，这个时候 16 位 Bit 中最左边的就不算符号位了，成了实际的数值存储位。对于结果不大于 16 的运算自然是可以储存的。

2、将 valueA、valueB、s 的类型变成 int，即将数据类型占用的内存空间变大（16 bit -> 32 bit），这样储存 16 位 Bit 的数据就绰绰有余了。

需要注意的是，在进行整数之间的运算时，不管你设置的数据类型占用的内存空间有多大，得到的结果都会有发生溢出的风险。溢出是一个异常的事件，我们在进行程序设计时，应当对输入数据的最大值和最小值有一个充分的预估，以避免溢出这种异常情况的产生。

这是计算机中运算和数学中一个很大的不同的地方，数学是理论，我们在草稿纸上计算时，如果有进位，我们就在左边加一位，这是没有空间限制的（只要你的草稿纸足够大）。

而计算机是应用。在包括 C语言在内的绝大多数编译语言中，每一个个变量能储存大多的数值在这个变量定义时就已经决定了。计算机中每一个信息都需要用储存介质（内存、磁盘）来进行储存，而这个介质的容量一定是有限的，当数据超过了这个容量后（在这里体现的就是数据类型占用的字节数），多余的数据就会丢失，而在没有其他处理的前提下，计算机就会按照原有既定的规则来处理这些不完整的数据，进而发生意想不到的结果。

好了，这篇文章到这里就结束了，我们详细介绍了 C语言中的数据类型，以及信息在计算机中的表示方式、编码方式，最后我们讨论了一下为什么计算机无法精确的表示某些小数。如果觉得本文对你有帮助，请不要吝啬你的赞，如果文章中有哪里不对的地方，请多多指点。

谢谢观看。。。

附录

1、Ascii 码字符对照表

Bin(二进制)	Oct(八进制)	Dec(十进制)	Hex(十六进制)	缩写/字符	解释
0000 0000	00	0	0x00	NUL(null)	空字符
0000 0001	01	1	0x01	SOH(start of headline)	标题开始
0000 0010	02	2	0x02	STX (start of text)	正文开始
0000 0011	03	3	0x03	ETX (end of text)	正文结束
0000 0100	04	4	0x04	EOT (end of transmission)	传输结束
0000 0101	05	5	0x05	ENQ (enquiry)	请求
0000 0110	06	6	0x06	ACK (acknowledge)	收到通知
0000 0111	07	7	0x07	BEL (bell)	响铃
0000 1000	010	8	0x08	BS (backspace)	退格
0000 1001	011	9	0x09	HT (horizontal tab)	水平制表符
0000 1010	012	10	0x0A	LF (NL line feed, new line)	换行键
0000 1011	013	11	0x0B	VT (vertical tab)	垂直制表符
0000 1100	014	12	0x0C	FF (NP form feed, new page)	换页键
0000 1101	015	13	0x0D	CR (carriage return)	回车键
0000 1110	016	14	0x0E	SO (shift out)	不用切换
0000 1111	017	15	0x0F	SI (shift in)	启用切换
0001 0000	020	16	0x10	DLE (data link escape)	数据链路转义
0001 0001	021	17	0x11	DC1 (device control 1)	设备控制1
0001 0010	022	18	0x12	DC2 (device control 2)	设备控制2
0001 0011	023	19	0x13	DC3 (device control 3)	设备控制3
0001 0100	024	20	0x14	DC4 (device control 4)	设备控制4
0001 0101	025	21	0x15	NAK (negative acknowledge)	拒绝接收
0001 0110	026	22	0x16	SYN (synchronous idle)	同步空闲
0001 0111	027	23	0x17	ETB (end of trans. block)	结束传输块
0001 1000	030	24	0x18	CAN (cancel)	取消
0001 1001	031	25	0x19	EM (end of medium)	媒介结束
0001 1010	032	26	0x1A	SUB (substitute)	代替
0001 1011	033	27	0x1B	ESC (escape)	换码(溢出)
0001 1100	034	28	0x1C	FS (file separator)	文件分隔符
0001 1101	035	29	0x1D	GS (group separator)	分组符
0001 1110	036	30	0x1E	RS (record separator)	记录分隔符
0001 1111	037	31	0x1F	US (unit separator)	单元分隔符
0010 0000	040	32	0x20	(space)	空格
0010 0001	041	33	0x21	!	叹号
0010 0010	042	34	0x22	"	双引号
0010 0011	043	35	0x23	#	井号
0010 0100	044	36	0x24	$	美元符
0010 0101	045	37	0x25	%	百分号
0010 0110	046	38	0x26	&	和号
0010 0111	047	39	0x27	’	闭单引号
0010 1000	050	40	0x28	(	开括号
0010 1001	051	41	0x29	)	闭括号
0010 1010	052	42	0x2A	*	星号
0010 1011	053	43	0x2B	+	加号
0010 1100	054	44	0x2C	,	逗号
0010 1101	055	45	0x2D	-	减号/破折号
0010 1110	056	46	0x2E	.	句号
0010 1111	057	47	0x2F	/	斜杠
0011 0000	060	48	0x30	0	字符0
0011 0001	061	49	0x31	1	字符1
0011 0010	062	50	0x32	2	字符2
0011 0011	063	51	0x33	3	字符3
0011 0100	064	52	0x34	4	字符4
0011 0101	065	53	0x35	5	字符5
0011 0110	066	54	0x36	6	字符6
0011 0111	067	55	0x37	7	字符7
0011 1000	070	56	0x38	8	字符8
0011 1001	071	57	0x39	9	字符9
0011 1010	072	58	0x3A	:	冒号
0011 1011	073	59	0x3B	;	分号
0011 1100	074	60	0x3C	<	小于
0011 1101	075	61	0x3D	=	等号
0011 1110	076	62	0x3E	>	大于
0011 1111	077	63	0x3F	?	问号
0100 0000	0100	64	0x40	@	电子邮件符号
0100 0001	0101	65	0x41	A	大写字母A
0100 0010	0102	66	0x42	B	大写字母B
0100 0011	0103	67	0x43	C	大写字母C
0100 0100	0104	68	0x44	D	大写字母D
0100 0101	0105	69	0x45	E	大写字母E
0100 0110	0106	70	0x46	F	大写字母F
0100 0111	0107	71	0x47	G	大写字母G
0100 1000	0110	72	0x48	H	大写字母H
0100 1001	0111	73	0x49	I	大写字母I
01001010	0112	74	0x4A	J	大写字母J
0100 1011	0113	75	0x4B	K	大写字母K
0100 1100	0114	76	0x4C	L	大写字母L
0100 1101	0115	77	0x4D	M	大写字母M
0100 1110	0116	78	0x4E	N	大写字母N
0100 1111	0117	79	0x4F	O	大写字母O
0101 0000	0120	80	0x50	P	大写字母P
0101 0001	0121	81	0x51	Q	大写字母Q
0101 0010	0122	82	0x52	R	大写字母R
0101 0011	0123	83	0x53	S	大写字母S
0101 0100	0124	84	0x54	T	大写字母T
0101 0101	0125	85	0x55	U	大写字母U
0101 0110	0126	86	0x56	V	大写字母V
0101 0111	0127	87	0x57	W	大写字母W
0101 1000	0130	88	0x58	X	大写字母X
0101 1001	0131	89	0x59	Y	大写字母Y
0101 1010	0132	90	0x5A	Z	大写字母Z
0101 1011	0133	91	0x5B	[	开方括号
0101 1100	0134	92	0x5C	\	反斜杠
0101 1101	0135	93	0x5D	]	闭方括号
0101 1110	0136	94	0x5E	^	脱字符
0101 1111	0137	95	0x5F	_	下划线
0110 0000	0140	96	0x60	`	开单引号
0110 0001	0141	97	0x61	a	小写字母a
0110 0010	0142	98	0x62	b	小写字母b
0110 0011	0143	99	0x63	c	小写字母c
0110 0100	0144	100	0x64	d	小写字母d
0110 0101	0145	101	0x65	e	小写字母e
0110 0110	0146	102	0x66	f	小写字母f
0110 0111	0147	103	0x67	g	小写字母g
0110 1000	0150	104	0x68	h	小写字母h
0110 1001	0151	105	0x69	i	小写字母i
0110 1010	0152	106	0x6A	j	小写字母j
0110 1011	0153	107	0x6B	k	小写字母k
0110 1100	0154	108	0x6C	l	小写字母l
0110 1101	0155	109	0x6D	m	小写字母m
0110 1110	0156	110	0x6E	n	小写字母n
0110 1111	0157	111	0x6F	o	小写字母o
0111 0000	0160	112	0x70	p	小写字母p
0111 0001	0161	113	0x71	q	小写字母q
0111 0010	0162	114	0x72	r	小写字母r
0111 0011	0163	115	0x73	s	小写字母s
0111 0100	0164	116	0x74	t	小写字母t
0111 0101	0165	117	0x75	u	小写字母u
0111 0110	0166	118	0x76	v	小写字母v
0111 0111	0167	119	0x77	w	小写字母w
0111 1000	0170	120	0x78	x	小写字母x
0111 1001	0171	121	0x79	y	小写字母y
0111 1010	0172	122	0x7A	z	小写字母z
0111 1011	0173	123	0x7B	{	开花括号
0111 1100	0174	124	0x7C	|	垂线
0111 1101	0175	125	0x7D	}	闭花括号
0111 1110	0176	126	0x7E	~	波浪号
0111 1111	0177	127	0x7F	DEL (delete)	删除