状态压缩DP
一、棋盘类(基于连通块的DP)
一些做题得到的Trick
-
题目要求四联通不能重复
(a & b) == 0 -
题目要求八联通不能重复
(a | b) 不存在相邻的两个1 -
判断是否存在至少两个相邻的1
bool check(int x){ for(int i=0;i<n;i++){ if(x>>i&1 && x>>i+1&1) return false; } return true; } -
状态DP的时间复杂度是: 状态数 * 状态转移量 , 一般都很大,但是满足条件的状态数不会很多。
-
如果空间不够,当每一行的状态只和上一行有关的时候可以使用滚动数组优化
f[i&1][j] +=f[i-1&1][b]; -
把一个01组成的数组变成一个二进制串对应的10进制数(玉米田)
int res=0; for(int i=0;i<m;i++){ int t;cin>>t; res+= t<<i; } -
将10进制数打印成二进制数
void print(int x){ vector<int>ans; for(int i=0;i<m;i++){ ans.push_back(x>>i&1); } reverse(ans.begin(),ans.end()); for(auto c:ans){ cout<<c<<""; } cout<<endl; } -
在状态转移时,不要写judge函数,
常数大直接用continue -
相邻的两个1中间至少隔2个0 (炮兵阵地)
bool check(int state) (感觉很万能) { for (int i = 0; i < m; i ++ ) if ((state >> i & 1) && ((state >> i + 1 & 1) || (state >> i + 2 & 1))) return false; return true; } 当时手写的 bool check(int x){//不能有连续的两个1 int cnt=0;//连续的0的个数 bool flag=1; for(int i=0;i<m;i++){ int t = x>>i&1; if(t){ if(flag){ flag=0; cnt=0; continue; } if(cnt<2)return false; cnt=0; } else{ cnt++; } } return true; } -
有矩阵限制的题 (炮兵阵地和玉米田)。
输入 PHPP PPHH PPPP PHPP PHHP for (int i = 1; i <= n; i ++ ) for (int j = 0; j < m; j ++ ) { char c; cin >> c; g[i] += (c == 'H') << j; 把字符转为01串。 } -
将 iii 的第 jjj 位(从右向左,从0开始计数),置 0 (最短Hamilton路径)
i -= (1<<j) -
将iii 的第 jjj 位,置1
i |= (1<<j) -
位运算的优先级比四则元素的优先级低,
&运算的优先级比==的优先级要低。if( (a&b) == 0 ) 与 if( (a&b) ==0 )不同。 f[(1<<n)-1][n-1] 与f[1<<n-1][n-1]不同。
1.AcWing 291. 蒙德里安的梦想
18点59分。
二刷发现不会写。不知道横竖应该怎么表示,不清楚状态如何表示(突然发现这是我基础课打卡的最后一题)。
长方形如何抽象成二进制?
将长方形进行抽象。
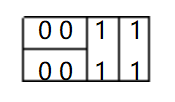
-
预处理出所有合法的条件。可以发现对于一个01串,连续的0必须是偶数个。
-
考虑如何DP,第 iii 层的状态依赖于第 i−1i-1i−1层的状态。 f[i][j]f[i][j]f[i][j] 表示已经摆放到第 iii 层,且第 i−1i-1i−1 层的状态是 jjj 的集合。
-
当上一层是 111 的时候,下一层只能放 111 。
枚举所有第i层合法的状态,递推。然后发现上边的状态表达式写不出来,改变状态表达式的定义:
f[i][j]f[i][j]f[i][j] 表示已经摆放到第 iii 层且第 iii 层的状态是 jjj 的所有方案的集合。
有一个很棘手的问题,我的ans是什么?我怎么知道最后一行能把所有的都摆满?
19:29:31第一题还没写完呢。
第一题SG代码
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 15;
int n,m;
bool st[1<<N];//将所有合法的01串标记出来
int f[N][N];
void print(int x){
vector<int>v;
for(int i=0;i<m;i++){
v.push_back(x>>i&1);
}
reverse(v.begin(),v.end());
for(auto c:v){
cout<<c;
}
cout<<endl;
}
bool check(int x,int y){
for(int i=0;i<m;i++){
if((x>>i&1) ^ (y>>i&1)){
return false;
}
}
return true;
}
int main(){
while(cin>>n>>m,n&&m){
for(int i=0;i<1<<m;i++){
int cnt=0;
st[i]=true;
for(int j=0;j<m;j++){
int t = i>>j;//数i的第j位(从右向左数)
if(t&1){
if(cnt&1){
st[i]=false;
break;
}
}
else{
cnt++;
}
}
if(cnt&1){
st[i]=false;
}
}
f[0][0]=1;
for(int i=1;i<=n+1;i++){
for(int j=0;j<1<<m;j++){
if(st[j]){
for(int k=0;k<1<<m;k++){
if(st[k]){
if(check(j,k)){
f[i][j] = f[i][j] + f[i-1][k];
}
}
}
}
}
}
cout<<f[n+1][0];
}
return 0;
}
看了下题解,发现和题解思路很 不一样,理解不了了。
开始二刷y总的视频。
没有想到的Trick:
- 按行把横着的小方块全都摆完,竖着的方块也就自动摆完了。所有方案数等于把横着的方块摆完的方案数。
而且主要到,题目要求把 N∗MN*MN∗M 的棋盘进行分割,所有要求所有横着的小方块摆完之后,竖着的小方块能够塞满。
- 发现了很多和我自己想的不同点,y总是按列摆的,我是按行摆的。y总定义 f[i][j]f[i][j]f[i][j] 表示已经摆完第 i−1i-1i−1 列,且第 i−1i-1i−1 列伸出到第 iii 列的方案是 jjj 的所有方案。(如果定义 jjj 就是第 iii 列的摆放方案,会发现子集不好划分。)子集划分,因为 第 i−1i-1i−1 到第 iii 列已经摆放好了,所以找最后一个不同点, 枚举第i−2i-2i−2 到 i−1i-1i−1 列的所有方案。 这个状态定义解决了一个非常棘手的问题,如何求ans
- 判断 jjj 和 kkk 何时满足条件。 jjj 和 kkk 在不同出现在同一行。
j & k == 0 - 对于每列考虑,因为塞的是横着的小方块,当把横着的小方块塞满之后,剩下的空着的连续小方块的个数必须是偶数,才能被 1∗21*21∗2 的方块塞满。
- 这题的状态定义非常有意思,他方便的最后答案的求解。如果从第 000 列开始计数,最后一列是 第m−1m-1m−1 列,答案就是 f[m][0]f[m][0]f[m][0] 已经将第 0∼m−10 \sim m-10∼m−1 列摆好,并且最后一列合法的所有方案的集合。
第二个三十分钟到了,我第一题还没写完。
大冤种了,遇到了优先级的BUG,以后不确定的优先级一定要写括号,不然调都不好调。
if ((j & k) == 0 && st[j | k]) 写成了 if((j&k==0)&&(st[j|k]))
等于和不等于比按位与的优先级高,按位与比按位异或和按位或的优先级高。 他们比&& , || 的优先级高。
三目运算符仅比 = ,+= ,/= ,*= , % , ... , 这些运算符的优先级高。
把所有的n改成m,就变成了按行放置的代码,可见按行还是按列都是可以的,我自己写的代码不行,是因为状态没定义好。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 15, M = 1 << N;
int n, m;
long long f[N][M];
bool st[M];
int main()
{
while (cin >> n >> m, n || m)
{
for (int i = 0; i < 1 << n; i ++ )
{
int cnt = 0;
st[i] = true;
for (int j = 0; j < n; j ++ )
if (i >> j & 1)
{
if (cnt & 1){
st[i] = false;
break;
}
cnt = 0;
}
else cnt ++ ;
if (cnt & 1) st[i] = false;
}
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= m; i ++ )
for (int j = 0; j < 1 << n; j ++ )
for (int k = 0; k < 1 << n; k ++ ) //可以把从 k->j 的合法情况预处理出来
if ((j & k) == 0 && st[j | k])
f[i][j] += f[i - 1][k];
cout << f[m][0] << endl;
}
return 0;
}
2.AcWing 1064. 小国王([SCOI2005]互不侵犯)(dfs+状态压缩DP)
忘记怎么思考了。
第三个30分钟到, 然后我发现可能当时就理解的不是很深刻吧。
放置国王的时候,第 iii 行如何放置只和第 i−1i-1i−1 行有关。
考虑状态定义 : f[i][j][s]f[i][j][s]f[i][j][s] 表示已经处理完了前 iii 行,且最后一行的状态是 jjj ,当前摆放了 sss 个国王的所有合法方案。
状态转移:枚举第 i−1i-1i−1 行,判断两个状态是否合法。
对于每个合法的状态要求:不能有两个相邻的1。
定义: aaa 表示第 iii 行的状态,bbb 表示第 i−1i-1i−1 行的状态。
- 同一列不能有俩国王。
a & b ==0 - 两行的国王不能互相攻击到。
(a|b) 满足不能有两个相邻的1
然后考虑状态转移方程。
对于 f[i][j][s]f[i][j][s]f[i][j][s] ,我们枚举的是第 i−1i-1i−1 排的状态。
第i排的状态是j,第i−1排的状态是a,count(j)表示状态j中国王的个数f[i][j][s]+=f[i−1][a][s−count(j)]或者写成f[i+1][j][s]+=f[i][a][s−count(j)]
第i排的状态是j,第i-1排的状态是a,count(j)表示状态j中国王的个数\\
f[i][j][s] += f[i-1][a][s-count(j)] \\
或者写成\\
f[i+1][j][s] += f[i][a][s-count(j)] \\
第i排的状态是j,第i−1排的状态是a,count(j)表示状态j中国王的个数f[i][j][s]+=f[i−1][a][s−count(j)]或者写成f[i+1][j][s]+=f[i][a][s−count(j)]
才发现忘了开闹钟了
什么是答案呢?
自己写了一个dfs+状态压缩DP的代码
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
const int N = 12;
int n,k;
int f[N][1<<N][N];
bool st[1<<N];//所有满足条件数量
ll ans=0;
int cal(int x){//返回一行中国王的个数。
int res=0;
for(int i=0;i<n;i++){
if(x>>i&1)res++;
}
return res;
}
bool check(int a,int b){
int x = a|b;
for(int j=0;j<n;j++){
if(x>>j&1&&(x>>j+1&1)){
return false;
}
}
return true;
}
//我是用第i层去推第i+1层,和状态转移方程有点偏差。
void dfs(int u,int state,int num){//已经摆放完第i行,第i行的状态是state,已经摆放了num个国王。
// 顺序写的有点问题。
if(u>n){
if(num==k){
ans++;
}
else{
return ;
}
}
//枚举第i-1行的所有状态
for(int j=0;j<1<<n;j++){
int a = state;
int b = j;
if(a&b==0 && check(a,b)){
dfs(u+1,b,num+cal(b));
}
}
}
int main(){
cin>>n>>k;
//对于一行国王来说,不能有两个相邻的1
for(int i=0;i<1<<n;i++){
st[i]=true;
for(int j=0;j<n;j++){
if((i>>j&1) && (i>>(j+1)&1)){
st[i]=false;
}
}
}
for(int i=0;i<1<<n;i++){
if(st[i])
dfs(1,i,cal(i));//从第1行开始考虑,目前放置了cal(i)个国王
}
cout<<ans<<endl;
return 0;
}
改了但是没改的代码
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
const int N = 12;
int n,k;
int f[N][1<<N][N*N];
bool st[1<<N];//所有满足条件数量
ll ans=0;
int cal(int x){//返回一行中国王的个数。
int res=0;
for(int i=0;i<n;i++){
if(x>>i&1)res++;
}
return res;
}
bool check(int a,int b){
int x = a|b;
for(int j=0;j<n;j++){
if(x>>j&1&&(x>>j+1&1)){
return false;
}
}
return true;
}
//我是用第i层去推第i+1层,和状态转移方程有点偏差。
void dfs(int u,int state,int num){//已经摆放完第i行,第i行的状态是state,已经摆放了num个国王。
cout<<u<<" "<<state<<" "<<num<<endl;
if(u>n){
if(!k){
ans++;
}
else{
return ;
}
}
//枚举第i-1行的所有状态
for(int j=0;j<1<<n;j++){
int a = state;
int b = j;//第i+1层的状态
if(a&b==0 && check(a,b)){
dfs(u+1,b,num-cal(b));
}
}
}
int main(){
cin>>n>>k;
//对于一行国王来说,不能有两个相邻的1
for(int i=0;i<1<<n;i++){
st[i]=true;
for(int j=0;j<n;j++){
if((i>>j&1) && (i>>(j+1)&1)){
st[i]=false;
}
}
}
for(int i=0;i<1<<n;i++){
if(st[i])
dfs(1,i,k-cal(i));//从第1行开始考虑,目前放置了cal(i)个国王
}
cout<<ans<<endl;
return 0;
}
22:36:34终于写出来了少了一个条件人麻了
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long ll;
const int N = 12;
int n,m;
ll f[N][1<<N][N*N];
bool st[1<<N];//所有满足条件数量
ll ans=0;
int cal(int x){//返回一行中国王的个数。
int res=0;
for(int i=0;i<n;i++) res += x>>i&1;
return res;
}
bool check(int a,int b){
int x = a|b;
for(int j=0;j<n;j++){
if(x>>j&1&&(x>>j+1&1)){
return false;
}
}
return true;
}
vector<int>a;
vector<int>tran[1<<N];//每个合法的方案存储所有他可以转移到的方案。
void init(){
for(int i=0;i<1<<n;i++){
st[i]=true;
for(int j=0;j<n;j++){
if((i>>j&1) && (i>>(j+1)&1)){
st[i]=false;
}
}
if(st[i]){
a.push_back(i);//存储所有合法的方案。
}
}
for(int i=0;i<a.size();i++){//不能只添加单向边,需要添加双向边
for(int j=0;j<a.size();j++){
int x = a[i];
int y = a[j];
if((x&y)==0&&check(x,y)){//少了一个条件人麻了
tran[x].push_back(y);
}
}
}
}
int main(){
cin>>n>>m;
init();
f[0][0][0]=1;
for(int i=1;i<=n+1;i++){//第一维
for(int j=0;j<=m;j++){//第三维
for(int k=0;k<a.size();k++){//k表示第i行的状态
for(auto c:tran[a[k]]){//c表示第i行可以由哪些状态转移来
int cnt=cal(a[k]);//求一下第i行中国王的数量。
if(cnt<=j)
f[i][a[k]][j]+=f[i-1][c][j-cnt];
}
}
}
}
cout<<f[n+1][0][m]<<endl;
return 0;
}
3.AcWing 327. 玉米田
14:38:18
f[i][j]f[i][j]f[i][j] 表示种完了前 iii 行土地,且最后一行的状态是 jjj 的所有种植方案的集合。
枚举所有 i−1i-1i−1 行合法的种植方案,转移。
f[i][j]+=f[i−1][j′]f[i][j] += f[i-1][j']f[i][j]+=f[i−1][j′]
自己写的0分代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define debug(x) cout<<#x<<":"<<x<<endl
using namespace std;
typedef long long ll;
const int N = 15,mod = 1e8;
int m,n;
ll f[N][1<<N];
int st[N][N];
vector<int>state;
bool check(int x){//不能有连续的两个1
for(int i=0;i<n;i++){
if(x>>i&1 && x>>i+1 &1){
return false;
}
}
return true;
}
bool Chk(int id,int x){
if(!id)return true;
for(int i=0;i<n;i++){
int t = x>>i&1;
if(t!=st[id][n-i]){
return false;
}
}
return true;
}
int main(){
cin>>m>>n;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
cin>>st[i][j];
}
}
for(int i=0;i<1<<n;i++){
if(check(i)){
state.push_back(i);
}
}
f[0][0]=1;
for(int i=1;i<=m+1;i++){
for(int j=0;j<state.size();j++){//第i行
for(int k=0;k<state.size();k++){//i-1行
int x = state[j];
int y = state[k];
if((x&y)==0&&Chk(i,x)&&Chk(i-1,y)){
cout<<"?"<<endl;
f[i][x] = (f[i][x] + f[i-1][y])%mod;
}
}
}
}
cout<<f[m+1][0];
return 0;
}
第一个30分钟到了,还没找出BUG
一顿操作之后,发现第一个Chk写错了,改了就对了
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define debug(x) cout<<#x<<":"<<x<<endl
using namespace std;
typedef long long ll;
const int N = 15,mod = 1e8;
int m,n;
ll f[N][1<<N];
int st[N][N];
vector<int>state;
bool check(int x){//不能有连续的两个1
for(int i=0;i<n;i++){
if(x>>i&1 && x>>i+1 &1){
return false;
}
}
return true;
}
bool Chk(int id,int x){
if(!id)return true;
for(int i=0;i<n;i++){
int t = x>>i&1;
// debug(t);
// debug(st[id][n-i]);
if(t && !st[id][n-i]){
return false;
}
}
return true;
}
void print(int x){
vector<int>ans;
for(int i=0;i<n;i++){
ans.push_back(x>>i&1);
}
reverse(ans.begin(),ans.end());
for(auto c:ans){
cout<<c<<"";
}
cout<<endl;
}
int main(){
cin>>m>>n;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
cin>>st[i][j];
}
}
for(int i=0;i<1<<n;i++){
if(check(i)){
state.push_back(i);
}
}
f[0][0]=1;
for(int i=1;i<=m+1;i++){
for(int j=0;j<state.size();j++){//第i行
for(int k=0;k<state.size();k++){//i-1行
int x = state[j];
int y = state[k];
// cout<<i<<endl;
// print(x);print(y);
// cout<<i<<" Chk(x)=="<<Chk(i,x)<<endl;
// cout<<i-1<<" Chk(y)=="<<Chk(i-1,y)<<endl;
if((x&y)==0&&Chk(i,x)&&Chk(i-1,y)){
f[i][x] = (f[i][x] + f[i-1][y])%mod;
}
}
}
}
cout<<f[m+1][0];
return 0;
}
4.AcWing 292. 炮兵阵地
15:33:53
第2个30分钟到了,刚写炮兵阵地
f数组爆空间了,用滚动数组优化。
自己的0分代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define debug(x) cout<<#x<<":"<<x<<endl
using namespace std;
typedef long long ll;
const int N = 12,mod = 1e8;
int n,m;
char g[110][20];
vector<int>state;
vector<int>st[110];//每行有哪些状态是合法的
int f[2][1<<N][1<<N];
/*
每一行,1之间0的数量必须大于等于2
1 0 0 0 0 1
f[i][j][k];
摆放了i行,第i行是j,且第i-1行是k的所有摆放方案的集合。
*/
int cal(int x){
int res=0;
for(int i=0;i<m;i++){
res+= x>>i&1;
}
return res;
}
bool check(int x){//不能有连续的两个1
int cnt=0;//连续的0的个数
bool flag=1;
for(int i=0;i<m;i++){
int t = x>>i&1;
if(t){
if(flag){
flag=0;
cnt=0;
continue;
}
if(cnt<2)return false;
cnt=0;
}
else{
cnt++;
}
}
return true;
}
bool chk(int id,int x){
for(int i=0;i<m;i++){
int t = x>>i&1;
if(t&&g[id][m-i-1]=='H'){
return false;
}
}
return true;
}
void print(int x){
vector<int>ans;
for(int i=0;i<m;i++){
ans.push_back(x>>i&1);
}
reverse(ans.begin(),ans.end());
for(auto c:ans){
cout<<c<<"";
}
cout<<endl;
}
bool judge(int x,int y,int z){
if((x&y) || (x&z) || (y&z)) return false;//满足垂直关系
return true;
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
scanf("%s",g+i);
}
for(int i=0;i<1<<m;i++){
if(check(i)){
state.push_back(i);
}
}
for(int i=0;i<n;i++){
for(auto c:state){
if(chk(i,c)){
st[i].push_back(c);//从0下标开始的
}
}
}
for(int i=1;i<=n+2;i++){
for(auto a:st[i-1]){
for(auto b:st[i-2]){
for(auto c:st[i-3]){
if(judge(a,b,c)){
f[i&1][a][b] = max(f[i&1][a][b],f[i-1&1][b][c] +cal(a));
}
}
}
}
}
cout<<f[n+2&1][0][0]<<endl;
// int res = 0;
// for (int i = 0; i < state.size(); i ++ )
// for (int j = 0; j < state.size(); j ++ )
// res = max(res, f[n & 1][i][j]);
// cout << res << endl;
return 0;
}
第三个30分钟到了,我还在调BUG。
TM的,我又自己打自己的脸了
我的G数组从0行开始读的,取数字忘了++了
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define debug(x) cout<<#x<<":"<<x<<endl
using namespace std;
typedef long long ll;
const int N = 12,mod = 1e8;
int n,m;
char g[110][20];
vector<int>state;
int f[2][1<<N][1<<N];
/*
每一行,1之间0的数量必须大于等于2
1 0 0 0 0 1
f[i][j][k];
摆放了i行,第i行是j,且第i-1行是k的所有摆放方案的集合。
*/
int cal(int x){
int res=0;
for(int i=0;i<m;i++){
res+= x>>i&1;
}
return res;
}
bool check(int x){//不能有连续的两个1
int cnt=0;//连续的0的个数
bool flag=1;
for(int i=0;i<m;i++){
int t = x>>i&1;
if(t){
if(flag){
flag=0;
cnt=0;
continue;
}
if(cnt<2)return false;
cnt=0;
}
else{
cnt++;
}
}
return true;
}
bool chk(int id,int x){
for(int i=0;i<m;i++){
int t = x>>i&1;
if(t&&g[id][m-i-1]=='H'){
return false;
}
}
return true;
}
void print(int x){
vector<int>ans;
for(int i=0;i<m;i++){
ans.push_back(x>>i&1);
}
reverse(ans.begin(),ans.end());
for(auto c:ans){
cout<<c<<"";
}
cout<<endl;
}
bool judge(int id,int x,int y,int z){//倒数第1行,倒数第2行。
id--;
if((x&y) | (x&z) | (y&z)) return false;//满足垂直关系
if(!chk(id,x))return false;
if(!chk(id-1,y))return false;
if(!chk(id-2,z))return false;
return true;
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
scanf("%s",g+i);
}
for(int i=0;i<1<<m;i++){
if(check(i)){
state.push_back(i);
}
}
for(int i=1;i<=n+2;i++){
for(auto a:state){
for(auto b:state){
for(auto c:state){
if(judge(i,a,b,c)){
f[i&1][a][b] = max(f[i&1][a][b],f[i-1&1][b][c] +cal(a));
}
}
}
}
}
cout<<f[n+2&1][0][0]<<endl;
return 0;
}
最后一个点TLE了,把judge展开,卡常AC
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define debug(x) cout<<#x<<":"<<x<<endl
using namespace std;
typedef long long ll;
const int N = 12,mod = 1e8;
int n,m;
char g[110][20];
vector<int>state;
int f[2][1<<N][1<<N];
/*
每一行,1之间0的数量必须大于等于2
1 0 0 0 0 1
f[i][j][k];
摆放了i行,第i行是j,且第i-1行是k的所有摆放方案的集合。
*/
int cal(int x){
int res=0;
for(int i=0;i<m;i++){
res+= x>>i&1;
}
return res;
}
bool check(int x){//不能有连续的两个1
int cnt=0;//连续的0的个数
bool flag=1;
for(int i=0;i<m;i++){
int t = x>>i&1;
if(t){
if(flag){
flag=0;
cnt=0;
continue;
}
if(cnt<2)return false;
cnt=0;
}
else{
cnt++;
}
}
return true;
}
bool chk(int id,int x){
for(int i=0;i<m;i++){
int t = x>>i&1;
if(t&&g[id][m-i-1]=='H'){
return false;
}
}
return true;
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
scanf("%s",g+i);
}
for(int i=0;i<1<<m;i++){
if(check(i)){
state.push_back(i);
}
}
for(int i=1;i<=n+2;i++){
for(auto a:state){
for(auto b:state){
for(auto c:state){
if((a&b) | (b&c) | (a&c)) continue;//满足垂直关系
int id = i;
id--;
if(!chk(id,a))continue;
if(!chk(id-1,b))continue;
if(!chk(id-2,c))continue;
f[i&1][a][b] = max(f[i&1][a][b],f[i-1&1][b][c] +cal(a));
}
}
}
}
cout<<f[n+2&1][0][0]<<endl;
return 0;
}
P3694 邦邦的大合唱站队
人麻了,我暴力都写不利索。感觉打了20分钟才写了一个20%的暴力(然后TM全T了)。
看了题解后
第一篇题解没懂,看别人的题解
O(M!)算法O(M!)算法O(M!)算法
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
template<typename T>void read(T &r){static char c;r=0;for(c=getchar();c>'9'||c<'0';c=getchar());for(;c>='0'&&c<='9';r=(r<<1)+(r<<3)+(c^48),c=getchar());}
const int maxn = 1e5 + 10;
const int maxm = 21;
int n,m;
int a[maxn];
int num[maxm];
int order[maxm];
int s[maxn][maxm];
int main()
{
read(n);
read(m);
for(int i = 1;i<=n;++i)
read(a[i]),num[a[i]]++,s[i][a[i]]++;
for(int i = 1;i<=n;++i)
for(int j = 1;j<=m;++j)
s[i][j] += s[i-1][j];
for(int i = 1;i<=m;++i)
order[i] = i;
int ans = 1 << 30;
do
{
int res = 0;
int l = 0,r = 0;
for(int i = 1;i<=m;++i)
{
l = r + 1;
r = l + num[order[i]] - 1;
res += num[i] - (s[r][order[i]] - s[l-1][order[i]]);
}
ans = min(ans,res);
} while (next_permutation(order + 1, order + 1 + m));
printf("%d",ans);
return 0;
}
想要将 O(M!)O(M!)O(M!) 的复杂度降低到 O(2M)O(2^M)O(2M),使用状压DP的方法。
f[i]表示i的二进制中是1的组已经排好队了,该集合下出队次数的最小值f[i] 表示i的二进制中是1的组已经排好队了,该集合下出队次数的最小值f[i]表示i的二进制中是1的组已经排好队了,该集合下出队次数的最小值
f[i]只知道哪些乐队在里边,并不知道最后的顺序,可以枚举排在最后的组f[i] 只知道哪些乐队在里边,并不知道最后的顺序,可以枚举排在最后的组f[i]只知道哪些乐队在里边,并不知道最后的顺序,可以枚举排在最后的组
可以先预处理出每个组的队列长度,知道长度之后就知道最后的组的范围,然后用类似二维前缀和求出应该将多少人移除队列。
woc,真的自己AC了,蓝题不过如此 (核心就是0/1背包的思想)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define debug(x) cout<<#x<<":"<<x<<endl
using namespace std;
typedef long long ll;
const int N = 1e5+10,mod = 1e8;
int cnt[22];//每个乐队的人数
int id[N];
int n,m;
int s[N][22];//前i个人中每个乐队的人的个数
int f[1<<22];
int len[1<<22];
/*
预处理出每个队列的长度,我感觉我好懒啊,
一直想看人家的代码,都不自己思考着写。
*/
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>id[i];
cnt[id[i]]++;
s[i][id[i]]++;
}
for(int i=0;i<1<<m;i++){
for(int j=0;j<m;j++){
if((i>>j)&1){
len[i]+=cnt[j+1];
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
s[i][j]+=s[i-1][j];
}
}
memset(f,0x3f,sizeof f);
f[0]=0;
for(int i=0;i<1<<m;i++){
for(int j=0;j<m;j++){//让j跑到最后一队去
int t = (i>>j)&1;
if(!t)continue;
int length = len[i];//状态i时所有人的总长度
int r = length;
int l = length - cnt[j+1] + 1;
f[i] = min(f[i],f[i-(1<<j)] + cnt[j+1] - (s[r][j+1]-s[l-1][j+1]));
}
}
cout<<f[(1<<m)-1]<<endl;
return 0;
}
P3092 [USACO13NOV]No Change G(状态压缩DP+二分,前缀和)
很明显不是棋盘式DP,然后就G了。
暴力dfs?
dfs需要什么信息呢?样例告诉我们,先话面值小的硬币进行贪心不对。
看到题解的瞬间惊了(DP+二分?)
套路:硬币的数据范围只有16,所以压缩的肯定是硬币,可以把所有硬币的使用情况进行压缩。
看懂了一个大佬的题解,非常的妙,自己复现一下
f[i]f[i]f[i] 表示使用 iii 状态表示的硬币能够买到的最大层数。
c[i]表示i状态下是1的硬币的集合,用非常像背包的方式推递推式。c[i] 表示 i 状态下是1的硬币的集合,用非常像背包的方式推递推式。c[i]表示i状态下是1的硬币的集合,用非常像背包的方式推递推式。
不清楚数学怎么表达,看代码吧
麻了,手写lower_bound 写不出来
这题应该是找一个upper_bound
int find(ll cost){//写lower_bound
// 在sum数组中找<=s的最大的数的下标
int l=1,r=n;
while(l<r){
int mid=l+r>>1;
cout<<cost<<" "<<mid<<endl;
if(sum[mid]>=cost){// 用二分的值做判断, >= 就是大于等于x的第一个位置。
r=mid;
}
else{
l=mid+1;
}
}
return r;
}
手写upper_bound 也出错 (应该是写出来了,但是题目有特殊判断)
int find(ll cost){//手写upper_bound
// 在sum数组中找<=s的最大的数的下标
int l=1,r=n+1;
while(l<r){
int mid=l+r>>1;
if(sum[mid]>cost){
r=mid;
}
else{
l=mid+1;
}
}
return r;
}
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#define debug(x) cout<<#x<<":"<<x<<endl
using namespace std;
typedef long long ll;
const int N = 1e5+10,mod = 1e8;
int k,n;
ll a[N],w[20];
ll sum[N];
int dp[1<<17];
int find(ll cost){//手写upper_bound
// 在sum数组中找<=s的最大的数的下标
int l=1,r=n+1;
while(l<r){
int mid=l+r>>1;
if(sum[mid]>cost){
r=mid;
}
else{
l=mid+1;
}
}
return r;
}
int main(){
cin>>k>>n;
for(int i=0;i<k;i++){
cin>>w[i];
}
for(int i=1;i<=n;i++){
cin>>a[i];
sum[i] = sum[i-1] + a[i];
}
for(int i=0;i<1<<k;i++){//枚举所有的状态
for(int j=0;j<k;j++){//枚举硬币
if(!(i&(1<<j)))continue;
int pre = i^(1<<j);
pre = dp[pre];//很强
int pos=find(sum[pre]+w[j]);
dp[i] = max(dp[i],pos-1);
}
}
ll ans=-1;
for(int i=0;i<1<<k;i++){
if(dp[i]==n){
ll cost=0;
for(int j=0;j<k;j++){
if(!(i&(1<<j)))cost+=w[j];
}
ans=max(ans,cost);
}
}
cout<<ans<<endl;
return 0;
}
二、集合优化DP
1.AcWing 91. 最短Hamilton路径(旅行商问题,NPC)
二刷这道题的时候,发现完全没有思路。
现在来看依然是非常妙的一道题。
思路:把整条路径先拆分。我们想一笔画 nnn 个点,那么遍历过的点之后就不会再被遍历了。
假设我们要从 0到50 到 50到5 号点再到6号点(终点),如何拆分集合呢?找最后一个不同的位置
所有从0号店到5号点的方案可以划分为一个集合。这个集合中距离的最小值+ w[5][6]w[5][6]w[5][6] 就是问题可能的一组解。所以我们需要知道。
- 我们遍历了哪些点?
- 我们到了哪个点。
定义 f[i][j]f[i][j]f[i][j] 表示从0号点遍历到了 jjj 号点,且遍历的路径用二进制数表示为 iii 的所有方案的集合。
枚举最后一个不同点,kkk 是 jjj 的上一个点。
f[i][j]=min(f[i][j],f[i−1<<j][k]+w[k][j])f[i][j] = min(f[i][j],f[i-1<<j][k]+w[k][j])f[i][j]=min(f[i][j],f[i−1<<j][k]+w[k][j])
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 21;
int f[1<<21][N];
int n,a[N][N];
int main(){
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>a[i][j];
}
}
memset(f,0x3f,sizeof f);
f[0][0]=0;
for(int i=0;i<1<<n;i++){
for(int j=0;j<n;j++){
if(i>>j&1) //(需要注意的地方)
for(int k=0;k<n;k++){
if(i>>k&1)
// i的第j位置0
f[i][j] = min(f[i][j],f[i-(1<<j)][k]+a[k][j]);
}
}
}
cout<<f[ (1<<n) -1][n-1]<<endl;
return 0;
}





















 940
940

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








