题目:
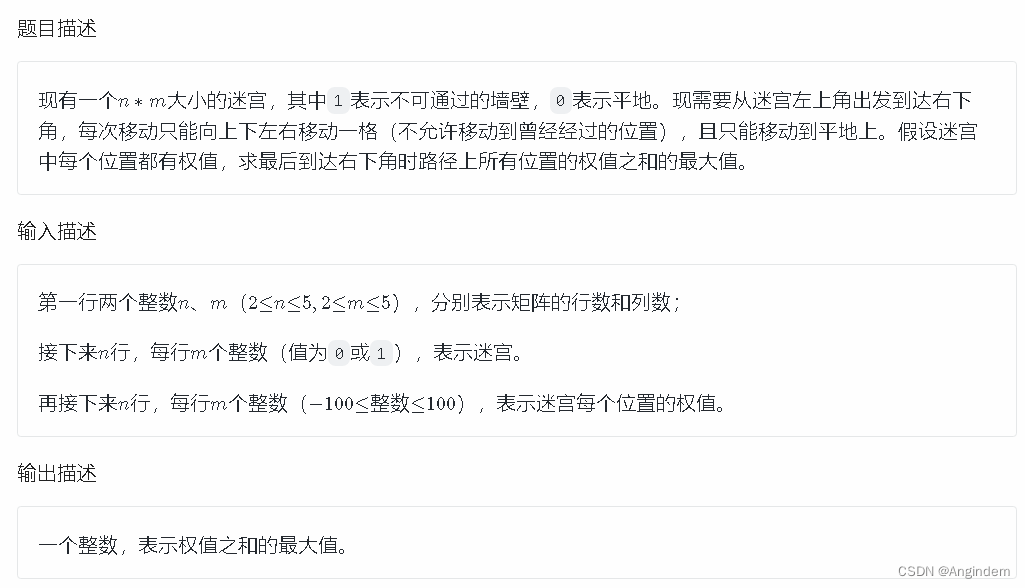
样例:
|
3 3 0 0 0 0 1 0 0 0 0 1 2 3 4 5 6 7 8 9 |
| 29 |
思路:
在这里,还是和走迷宫一样,只是多了一个权值累加然后比较即可
代码详解如下:
#include <iostream>
using namespace std;
const int N = 500;
// 这里是控制坐标移动操作,
// 错位即可一步一步的移动
int dx[4] = {1, 0, -1, 0};
int dy[4] = {0, 1, 0, -1};
int n, m; // 迷宫大小变量
int num[N][N]; // 数值矩阵
int g[N][N]; // 迷宫数组
bool vis[N][N]; // 这里是标记所走过的坐标
int ans = -0x3f3f; // 最终答案取最大值,所以这里我们要注意初始化无穷小
// 这里是 DFS 递归条件,也就是往前走的条件
bool isRun(int bx, int by)
{
return (bx >= 0 && bx < n && by >= 0 && by < m && !vis[bx][by] && !g[bx][by]);
}
void DFS(int x, int y, int sum)
{
// 递归边界,如果到达了右下角,判断数值总和大小
if (x == n - 1 && y == m - 1)
{
if (ans < sum)
{
ans = sum;
}
return ;
}
// 这里最容易让人忘记的
// 这里是标记当前的坐标,很关键
// 否则会多重复之前的走动
vis[x][y] = true;
for (int i = 0; i < 4; ++i)
{
int bx = x + dx[i];
int by = y + dy[i];
if (isRun(bx, by))
{
// 如果可以往前走的话
// 就开始累加,并且标记
vis[bx][by] = true;
DFS(bx, by, sum + num[bx][by]);
// 恢复原有状态
vis[bx][by] = false;
}
}
return ;
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
cin >> g[i][j];
}
}
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
cin >> num[i][j];
}
}
// 开始往前走
DFS(0, 0, num[0][0]);
cout << ans << endl;
return 0;
}
最后提交:





 该代码示例是一个C++程序,利用深度优先搜索(DFS)策略解决了一种特殊的迷宫问题。给定一个迷宫矩阵和一个数值矩阵,任务是找到从左上角到右下角的路径,使得路径上的数值之和最大。程序通过递归地遍历所有可能的路径并累加路径上的数值来实现这一目标。
该代码示例是一个C++程序,利用深度优先搜索(DFS)策略解决了一种特殊的迷宫问题。给定一个迷宫矩阵和一个数值矩阵,任务是找到从左上角到右下角的路径,使得路径上的数值之和最大。程序通过递归地遍历所有可能的路径并累加路径上的数值来实现这一目标。

















 1078
1078










