题目: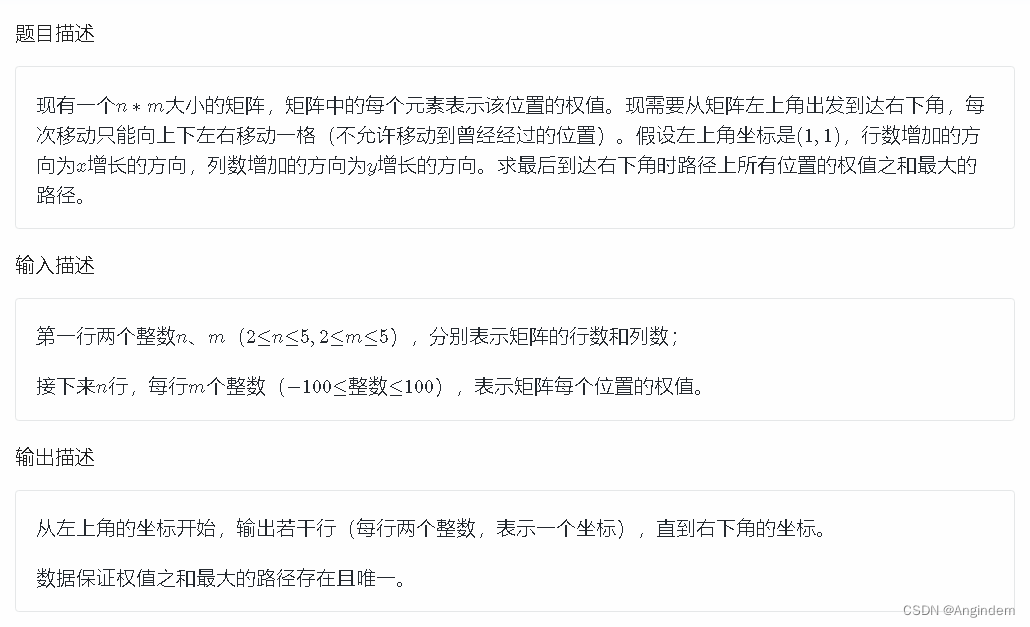
样例:
|
2 2 1 2 3 4 |
|
1 1 2 1 2 2 |
思路:
由于数据范围小,所以还是可以DFS暴力搜索,而这里将总和进行比较,然后在走动过程中统计好所走过的路径,再然后一旦有比上一条路径结果还要大的数值,那么就记录好最终路径即可
代码详解如下:
#include <iostream>
#include <vector>
#define mk make_pair // 自定义创建坐标变量名 为 mk
#define x first // 自定义坐标变量
#define y second
using namespace std;
const int N = 500;
using PII = pair<int, int>; // 自定义变量名 PII 为坐标
// 这里是控制坐标移动操作,
// 错位即可一步一步的移动
int dx[4] = {1, 0, -1, 0};
int dy[4] = {0, 1, 0, -1};
int n, m; // 矩阵大小变量
int g[N][N]; // 数值矩阵
bool vis[N][N]; // 这里是标记所走过的坐标
int ans_sum = -0x3f3f; // 最终答案取最大值,所以这里我们要注意初始化无穷小
vector<PII>tree, ans; // tree 为记录 DFS 路径 ans 为答案最终路径
// 这里是 DFS 递归条件,也就是往前走的条件
bool isRun(int bx, int by)
{
return (bx >= 0 && bx < n && by >= 0 && by < m && !vis[bx][by]);
}
void DFS(int x, int y, int sum)
{
// 递归边界,如果到达了右下角,判断数值总和大小
if (x == n - 1 && y == m - 1)
{
if (ans_sum < sum)
{
ans_sum = sum;
ans = tree;
}
return ;
}
// 这里最容易让人忘记的
// 这里是标记当前的坐标,很关键
// 否则会多重复之前的走动
vis[x][y] = true;
for (int i = 0; i < 4; ++i)
{
int bx = x + dx[i];
int by = y + dy[i];
if (isRun(bx, by))
{
// 如果可以往前走的话
// 就开始累加,并且标记
vis[bx][by] = true;
tree.emplace_back(mk(bx, by));
DFS(bx, by, sum + g[bx][by]);
// 恢复原有状态
tree.pop_back();
vis[bx][by] = false;
}
}
return ;
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
cin >> g[i][j];
}
}
// 因为肯定是从左上角开始,
// 所以先统计左上角的
tree.emplace_back(mk(0, 0));
// 开始往前走
DFS(0, 0, g[0][0]);
// 输出结果
for (auto i : ans)
{
cout << i.x + 1 << ' ' << i.y + 1 << endl;
}
return 0;
}
最后提交:





 该程序使用深度优先搜索(DFS)策略,通过暴力搜索找到一个二维矩阵中从左上角到右下角的最大路径和。在搜索过程中,它跟踪经过的坐标,更新最大路径和,并在找到更优解时保存路径。矩阵的每个单元格的值被累加到路径和中。最后,输出最优路径的坐标。
该程序使用深度优先搜索(DFS)策略,通过暴力搜索找到一个二维矩阵中从左上角到右下角的最大路径和。在搜索过程中,它跟踪经过的坐标,更新最大路径和,并在找到更优解时保存路径。矩阵的每个单元格的值被累加到路径和中。最后,输出最优路径的坐标。

















 903
903

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








