C++-二叉树OJ题

1. 二叉树创建字符串

OJ链接：606. 根据二叉树创建字符串 - 力扣（LeetCode）

思路： 

1. 前序遍历：按照根节点 -> 左子树 -> 右子树的顺序遍历二叉树。

2. 括号规则：

   • 如果当前节点的左孩子为空，但右孩子不为空，需要用 "()" 表示左孩子为空（以区分左右子树）。

   • 如果当前节点的右孩子为空，可以省略右孩子的空括号 "()"。

   • 如果当前节点的左右孩子都为空，可以完全省略括号。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    string tree2str(TreeNode* root) {
        if(root == nullptr) return "";    //递归终止条件
        if(root->left == nullptr && root->right == nullptr)
        {
            return to_string(root->val);
        }
        if(root->right == nullptr)
        {
            return to_string(root->val)+"("+tree2str(root->left)+")";
        }
        return to_string(root->val)
                +"("+tree2str(root->left)+")"
                +"("+tree2str(root->right)+")";

    }
};

代码解释

• 递归终止：

       空节点返回空字符串。

•    左右子树均为空：

        叶子节点返回节点值的字符串。

• 左子树处理：

        1、如果左子树或右子树存在，递归处理左子树并用括号包裹。

        2、如果左子树为空但右子树存在，会生成 "()"（占位左子树）。

• 右子树处理：

        只有右子树存在时才递归处理右子树并用括号包裹。

2. 二叉树的分层遍历1

OJ链接:102. 二叉树的层序遍历 - 力扣（LeetCode）

思路：

        二叉树的层序遍历（Level Order Traversal）是一种广度优先搜索（BFS）的应用，需要逐层访问节点，从左到右输出每一层的节点值。以下是实现层序遍历的步骤：

1. 初始化：使用队列来辅助遍历，首先将根节点入队。

2. 逐层处理：

   • 记录当前层的节点数量（队列的大小）。

   • 遍历当前层的所有节点，将它们的值存入结果中，并将它们的左右子节点（如果存在）入队。

3. 更新层信息：处理完当前层后，更新下一层的节点数量（即队列的新大小）。

4. 终止条件：当队列为空时，遍历结束。

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> vv; // 存储最终结果的二维数组
        if (root == NULL) return vv; // 空树直接返回
        
        queue<TreeNode*> q; // 辅助队列，用于BFS
        size_t levelsize = 1; // 初始层大小为1（根节点）
        
        q.push(root); // 根节点入队
        while (!q.empty()) { // 队列不为空时循环
            vector<int> v; // 存储当前层的节点值
            for (size_t i = 0; i < levelsize; ++i) { // 遍历当前层的所有节点
                TreeNode* front = q.front(); // 取出队首节点
                v.push_back(front->val); // 将节点值存入当前层的结果
                q.pop(); // 弹出已处理的节点
                
                // 将左右子节点入队（如果存在）
                if (front->left) q.push(front->left);
                if (front->right) q.push(front->right);
            }
            vv.push_back(v); // 将当前层的结果存入最终结果
            levelsize = q.size(); // 更新下一层的节点数量
        }
        return vv; // 返回层序遍历结果
    }
};

代码解释：

1. 队列的作用：队列用于按层级顺序存储待访问的节点，确保每一层的节点按从左到右的顺序处理。

2. 层大小的记录：levelsize 记录当前层的节点数量，确保内层循环只处理当前层的节点。

3. 子节点的入队：在处理当前层节点时，将其左右子节点（非空）入队，为下一层的遍历做准备。

4. 时间复杂度：O(N)，每个节点被访问一次。

5. 空间复杂度：O(N)，队列的最大空间为最后一层的节点数（最坏情况下为 O(N)）。

3. 二叉树的分层遍历2

OJ链接:107. 二叉树的层序遍历 II - 力扣（LeetCode）

思路：

       对于这道题我们可以惊奇的发现，思路与上面二叉树的分层遍历1思路基本相同，只需在他的代码最后加一个翻转即可

class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) 
    {
        vector<vector<int>> vv;
        if(root==NULL)
        return vv;
        queue<TreeNode*> q;
        size_t levelsize=1;

        q.push(root);
        while(!q.empty())
        {
            vector<int> v;
            for(size_t i=0;i<levelsize;++i)
            {
                
                TreeNode* front=q.front();
                v.push_back(front->val);
                q.pop();
                if(front->left)
                    q.push(front->left);
                if(front->right)
                    q.push(front->right);
            }
            vv.push_back(v);
            levelsize=q.size();
        }
        reverse(vv.begin(),vv.end()); //翻转vector容器
        return vv;
    }
};

4. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先

OJ链接:236. 二叉树的最近公共祖先 - 力扣（LeetCode）

思路：

1. 基本情况：如果当前节点为空或是 p/q 中的一个，直接返回当前节点

2. 递归搜索：分别在左右子树中搜索 p 和 q

3. 结果判断：

   • 如果左右子树都返回非空节点，说明当前节点就是 LCA

   • 如果只有一边返回非空，返回该结果（说明 LCA 在子树中）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 基本情况：如果root为空或是p/q中的一个，返回root
        if (root == nullptr || root == p || root == q) return root;
        
        // 在左右子树中查找p和q
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        
        // 如果左右都找到，说明当前节点是LCA
        if (left && right) return root;
        
        // 否则返回非空的那个结果
        return left ? left : right;
    }
};

代码解释：

• 递归法

• 时间复杂度：O(n)，每个节点最多访问一次

• 空间复杂度：O(n)，最坏情况下递归栈的深度等于树的高度

5. 二叉树搜索树转换成排序双向链表

OJ链接:二叉搜索树与双向链表_牛客题霸_牛客网

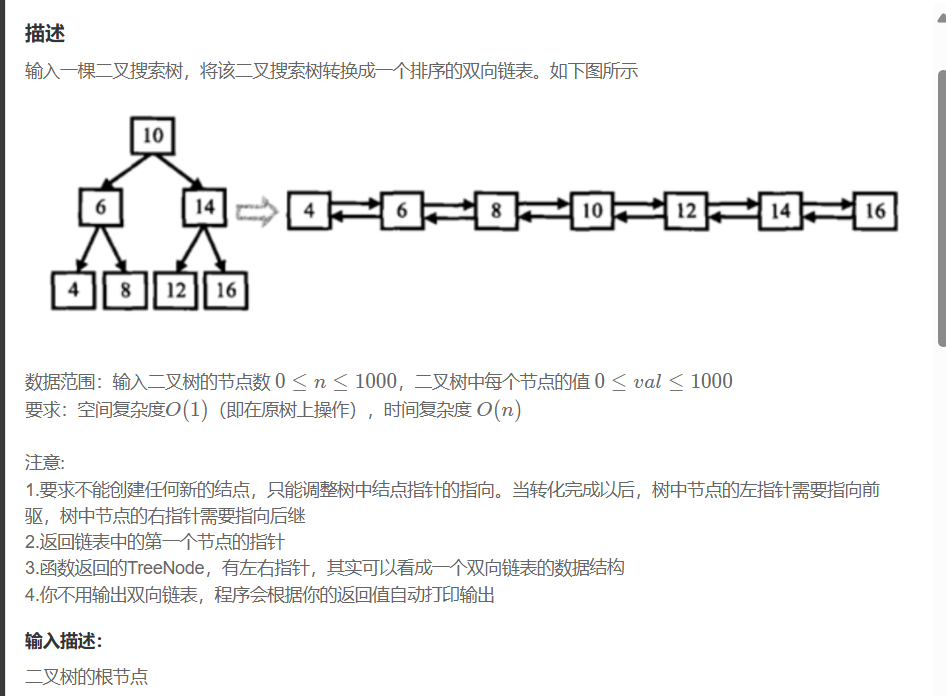
思路：

由于二叉搜索树的中序遍历结果是有序的，我们可以利用这一特性：

1. 使用中序遍历访问所有节点

2. 在遍历过程中维护一个"前驱节点"指针，将当前节点与前驱节点连接起来

3. 最后需要将头节点和尾节点连接起来（虽然题目示例似乎没有这个要求）

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
	void Solve(TreeNode* cur,TreeNode*& pre)
	{
		if(cur == nullptr) return;

		Solve(cur->left,pre);

		cur->left=pre;
		if(pre != nullptr)
		{
			pre->right = cur;
		}

		pre = cur; // 更新前驱节点

		Solve(cur->right,pre);
		return;
	}

    TreeNode* Convert(TreeNode* pRootOfTree) 
	{
		if(pRootOfTree == nullptr) return nullptr;
		//构造双链表
		TreeNode* pre = nullptr;
		Solve(pRootOfTree,pre);
		//找头节点
		TreeNode* head = pRootOfTree;
		while(head->left != nullptr)
		{
			head = head->left;
		}

		return head;
    }
};

代码解释：

1. 主函数 Convert：

   • 处理空树情况

   • 调用辅助函数进行转换

   • 寻找并返回链表头节点（最左节点）

2. 辅助函数 Solve：

   • 递归处理左子树

   • 将当前节点的左指针指向前驱节点

   • 如果前驱节点存在，将其右指针指向当前节点

   • 更新前驱节点为当前节点

   • 递归处理右子树

3. 指针处理：

   • 使用TreeNode*& pre（引用指针）来确保在整个递归过程中维护同一个前驱节点

• 时间复杂度：O(n)，需要访问所有节点一次

• 空间复杂度：O(1)，除了递归栈空间外没有使用额外空间

6. 根据一棵树的前序遍历与中序遍历构造二叉树

OJ链接:105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）

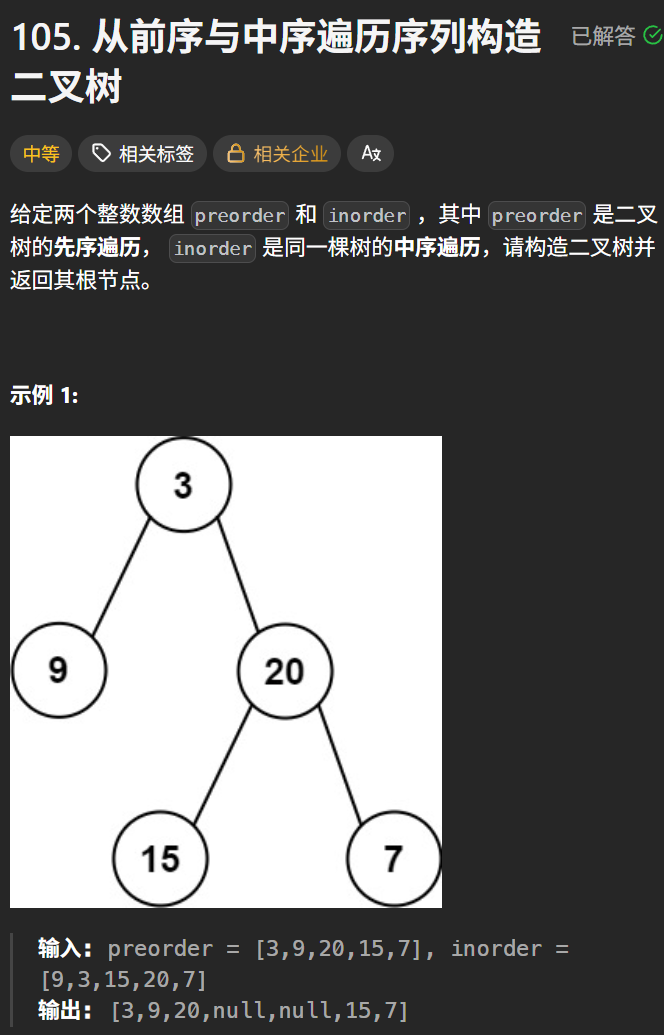
思路：

• 前序遍历的第一个元素总是树的根节点
• 在中序遍历中，根节点将序列分为左子树和右子树
• 递归地对左子树和右子树重复这个过程

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int preIndex = 0;
        return _buildTree(preorder, inorder, preIndex, 0, inorder.size()-1);
    }
    
    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder,
                       int& preIndex, int inStart, int inEnd) {
        if (inStart > inEnd) {
            return nullptr;
        }
        
        // 当前子树的根节点是前序遍历的第一个元素
        TreeNode* root = new TreeNode(preorder[preIndex]);
        
        // 在中序遍历中找到根节点的位置
        int inIndex = inStart;
        while (inIndex <= inEnd) {
            if (inorder[inIndex] == preorder[preIndex]) {
                break;
            }
            inIndex++;
        }
        
        // 移动到前序遍历的下一个元素
        preIndex++;
        
        // 递归构建左子树和右子树
        root->left = _buildTree(preorder, inorder, preIndex, inStart, inIndex-1);
        root->right = _buildTree(preorder, inorder, preIndex, inIndex+1, inEnd);
        
        return root;
    }
};

代码解释：

• 使用preIndex跟踪前序遍历中当前根节点的位置

• 在inorder数组中找到根节点的位置inIndex

• 左子树的范围是[inStart, inIndex-1]

• 右子树的范围是[inIndex+1, inEnd]

• 当inStart > inEnd时，表示当前子树为空，返回nullptr

• 时间复杂度：O(n)，每个节点只被处理一次

• 空间复杂度：O(n)，递归调用栈的深度在最坏情况下为n

7. 根据一棵树的中序遍历与后序遍历构造二叉树

OJ链接:106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）

思路：  

1. 后序遍历的特点：最后一个元素是根节点。

2. 中序遍历的特点：根节点将序列分为左子树和右子树。

3. 递归构建：

   • 从 postorder 中取出最后一个元素作为根节点。

   • 在 inorder 中找到根节点的位置，分割出左子树和右子树的 inorder 序列。

   • 根据左子树的长度，分割 postorder 序列为左子树和右子树的 postorder 序列。

   • 递归构建左子树和右子树。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        return build(inorder, 0, inorder.size() - 1, postorder, 0, postorder.size() - 1);
    }

    TreeNode* build(vector<int>& inorder, int inStart, int inEnd, vector<int>& postorder, int postStart, int postEnd) {
        if (inStart > inEnd || postStart > postEnd) {
            return nullptr;
        }

        // 根节点是 postorder 的最后一个元素
        int rootVal = postorder[postEnd];
        TreeNode* root = new TreeNode(rootVal);

        // 在 inorder 中找到根节点的位置
        int rootIndex = inStart;
        while (rootIndex <= inEnd && inorder[rootIndex] != rootVal) {
            rootIndex++;
        }

        // 左子树的长度
        int leftSize = rootIndex - inStart;

        // 递归构建左子树和右子树
        root->left = build(inorder, inStart, rootIndex - 1, postorder, postStart, postStart + leftSize - 1);
        root->right = build(inorder, rootIndex + 1, inEnd, postorder, postStart + leftSize, postEnd - 1);

        return root;
    }
};

代码解释：

1. 函数定义：

   • buildTree 是主函数，调用 build 辅助函数完成递归构建。

   • build 函数接收 inorder 和 postorder 的起始和结束索引，返回当前子树的根节点。

2. 递归终止条件：

   • 如果 inStart > inEnd 或 postStart > postEnd，说明当前子树为空，返回 nullptr。

3. 根节点确定：

   • postorder[postEnd] 是当前子树的根节点值。

4. 中序遍历分割：

   • 在 inorder 中找到根节点的位置 rootIndex，分割出左子树和右子树的 inorder 序列。

5. 后序遍历分割：

   • 左子树的 postorder 序列从 postStart 开始，长度为 leftSize。

   • 右子树的 postorder 序列从 postStart + leftSize 开始，到 postEnd - 1 结束（排除根节点）。

6. 递归构建：

   • 分别递归构建左子树和右子树，连接到当前根节点。

7. 时间复杂度：O(n)，每个节点被处理一次。

8. 空间复杂度：O(n)，递归栈的深度最坏为树的高度（线性退化为链表时为 O(n)）。

8. 二叉树的前序遍历，非递归迭代实现

OJ链接:144. 二叉树的前序遍历 - 力扣（LeetCode）

思路：

        按照 根节点 -> 左子树 -> 右子树 的顺序访问所有节点，并返回节点值的列表。

        利用栈模拟递归，显式地维护待处理的节点，优先访问根节点和左子树，再回溯处理右子树。

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> v; // 存储遍历结果
        stack<TreeNode*> s; // 辅助栈
        TreeNode* cur = root; // 当前节点
        while (cur || !s.empty()) {
            // 1. 访问左路节点，并入栈
            while (cur) {
                s.push(cur);
                v.push_back(cur->val); // 访问根节点
                cur = cur->left; // 转向左子树
            }
            // 2. 栈顶节点的右子树
            TreeNode* top = s.top();
            s.pop();
            cur = top->right; // 转向右子树
        }
        return v;
    }
};

代码解释：

1. 初始化：

   • vector<int> v：用于存储遍历结果。

   • stack<TreeNode*> s：辅助栈，用于模拟递归调用栈。

   • TreeNode* cur = root：从根节点开始遍历。

2. 外层循环：

   • 条件 cur || !s.empty()：只要当前节点不为空或栈不为空，就继续遍历。

     • cur 不为空：说明还有左子树或右子树需要处理。

     • !s.empty()：说明栈中还有未处理完的节点。

3. 内层循环（访问左路节点）：

   • while (cur)：沿着左子树深入，直到左子树为空。

     • 将当前节点 cur 的值存入结果列表 v（前序遍历的“根”操作）。

     • 将 cur 压入栈中（用于后续回溯）。

     • 转向左子树：cur = cur->left。

4. 处理右子树：

   • 当左子树为空时，从栈中弹出栈顶节点 top。

   • 转向右子树：cur = top->right。

   • 如果右子树不为空，下一次循环会继续处理右子树的左路节点。

5. 时间复杂度：O(n)，每个节点被访问一次。

6. 空间复杂度：O(n)，最坏情况下栈的空间为树的高度（线性退化为链表时为 O(n)）。

9. 二叉树中序遍历 ，非递归迭代实现

OJ链接:94. 二叉树的中序遍历 - 力扣（LeetCode）

思路：

        按照 左子树 -> 根节点 -> 右子树 的顺序访问所有节点，并返回节点值的列表。

        利用栈模拟递归，显式地维护待处理的节点，优先深入左子树，再访问根节点，最后处理右子树。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> v; // 存储遍历结果
        stack<TreeNode*> s; // 辅助栈
        TreeNode* cur = root; // 当前节点
        while (cur || !s.empty()) {
            // 1. 访问左路节点，并入栈
            while (cur) {
                s.push(cur);
                cur = cur->left; // 转向左子树
            }
            // 2. 栈顶节点的根节点和右子树
            TreeNode* top = s.top();
            v.push_back(top->val); // 访问根节点
            s.pop();
            cur = top->right; // 转向右子树
        }
        return v;
    }
};

代码解释：

1. 初始化：

   • vector<int> v：用于存储遍历结果。

   • stack<TreeNode*> s：辅助栈，用于模拟递归调用栈。

   • TreeNode* cur = root：从根节点开始遍历。

2. 外层循环：

   • 条件 cur || !s.empty()：只要当前节点不为空或栈不为空，就继续遍历。

     • cur 不为空：说明还有左子树或右子树需要处理。

     • !s.empty()：说明栈中还有未处理完的节点。

3. 内层循环（访问左路节点）：

   • while (cur)：沿着左子树深入，直到左子树为空。

     • 将当前节点 cur 压入栈中（用于后续回溯）。

     • 转向左子树：cur = cur->left。

4. 处理根节点和右子树：

   • 当左子树为空时，从栈中弹出栈顶节点 top。

   • 访问根节点：v.push_back(top->val)（中序遍历的“根”操作）。

   • 转向右子树：cur = top->right。

   • 如果右子树不为空，下一次循环会继续处理右子树的左路节点。

5. 时间复杂度：O(n)，每个节点被访问一次。

6. 空间复杂度：O(n)，最坏情况下栈的空间为树的高度（线性退化为链表时为 O(n)）。

10. 二叉树的后序遍历 ，非递归迭代实现

OJ链接:145. 二叉树的后序遍历 - 力扣（LeetCode）

思路：

        按照 左子树 -> 右子树 -> 根节点 的顺序访问所有节点，并返回节点值的列表。

        利用栈模拟递归，显式地维护待处理的节点，优先深入左子树，再处理右子树，最后访问根节点。通过 prev 标记已访问的右子树，避免重复访问。

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> v; // 存储遍历结果
        stack<TreeNode*> s; // 辅助栈
        TreeNode* cur = root; // 当前节点
        TreeNode* prev = nullptr; // 记录前一个访问的节点
        while (cur || !s.empty()) {
            // 1. 访问左路节点，并入栈
            while (cur) {
                s.push(cur);
                cur = cur->left;
            }
            // 2. 检查栈顶节点的右子树
            TreeNode* top = s.top();
            if (top->right == nullptr || prev == top->right) {
                // 右子树已访问或为空，可以访问根节点
                prev = top;
                v.push_back(top->val); // 访问根节点
                s.pop();
            } else {
                // 转向右子树
                cur = top->right;
            }
        }
        return v;
    }
};

代码解释：

1. 初始化：

   • vector<int> v：用于存储遍历结果。

   • stack<TreeNode*> s：辅助栈，用于模拟递归调用栈。

   • TreeNode* cur = root：从根节点开始遍历。

   • TreeNode* prev = nullptr：记录前一个访问的节点，用于判断右子树是否已访问。

2. 外层循环：

   • 条件 cur || !s.empty()：只要当前节点不为空或栈不为空，就继续遍历。

     • cur 不为空：说明还有左子树或右子树需要处理。

     • !s.empty()：说明栈中还有未处理完的节点。

3. 内层循环（访问左路节点）：

   • while (cur)：沿着左子树深入，直到左子树为空。

     • 将当前节点 cur 压入栈中（用于后续回溯）。

     • 转向左子树：cur = cur->left。

4. 处理右子树和根节点：

   • 当左子树为空时，检查栈顶节点 top 的右子树：

     • 如果 top->right == nullptr 或 prev == top->right（右子树已访问），则访问根节点 top->val，并弹出栈顶节点。

     • 否则，转向右子树：cur = top->right。

5. 时间复杂度：O(n)，每个节点被访问一次。

6. 空间复杂度：O(n)，最坏情况下栈的空间为树的高度（线性退化为链表时为 O(n)）。