数据结构-堆-C语言

前言：

 1.概念：

        堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的    数组对象。

 2.性质：

        1.堆中某个结点的值总是不大于或不小于其父结点的值；

        2.堆总是一棵完全二叉树。

        3.将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。常见的堆有  二叉堆、斐波那契堆等。

        4.堆的物理结构本质上是顺序存储的，是线性的。但在逻辑上不是线性的，是完全二叉树的这种逻辑储存结构。 堆的这个数据结构，里面的成员包括：一维数组，数组的容量，数组元素的个  数，有两个直接后继。

  大堆的代码实现：

        堆的实现所需要的基本操作主要有初始化，插入（这里需要用到向上调整），删除（这里需要用到向下调整），堆顶元素 , 判空，统计堆中元素个数

        因此，我们可以通过三个文件来实现一个堆。

其中：

        头文件-Heap.h：主要用来实现所需函数的声明以及include的调用。

        源文件-Heap.c：主要用来实现所需函数的定义。

        源文件-Test.c：主要用于检测和调用各个函数。

1.头文件-Heap.h：

        

         对于 头文件-Head.h 我们主要目的是在该文件中实现 初始化，销毁释放，判空，插入，删出，堆中元素个数，返回堆顶元素 这些函数的声明。我们还需在头文件内定义一下结构体的内部结构当然也可以通过typedef使结构体名字简化,这里我是通过数组来实现的堆，所以这里我定义了一个结构体用来存储 数组a,数组大小，容量。除此之外，我们还需要调用各个函数定义所需要的头文件。如 stdio.h , stdlib.h , assert.h ,stdbool.h 等。

代码如下：

#pragma once

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>

//大堆
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;

void HeapInit(HP* php);				//初始化
void HeapDestory(HP* php);           //释放销毁
void HeapPush(HP* php, HPDataType x);				//插入
void HeapPop(HP* php);				//删除
HPDataType HeapTop(HP* php);							//堆顶元素	
bool HeapEmpty(HP* php);			//判空
int HeapSize(HP* php);				//堆中元素个数

2.源文件-Heap.c：

初始化-HeapInit：

        这里传入了结构体指针，该指针不能为空，故这里需要通过断言来增强代码的健壮性。然后我们为数组a开辟空间并判断空间是否开辟成功，接着对结构体其他成员进行初始化即可。我这里容量初始化值为4。

代码如下：

void HeapInit(HP* php)				//初始化
{
	assert(php);

	php->a = (HPDataType*)malloc(sizeof(HPDataType)*4);
	if (php->a == NULL)
	{
		perror("malloc");
		return;
	}

	php->size = 0;
	php->capacity = 4;
}

销毁释放-HeapDestory：

        这里传入了结构体指针，该指针不能为空，故这里需要通过断言来增强代码的健壮性。然后我们需将开辟的空间均释放掉。

代码如下：

void HeapDestory(HP* php)           //释放销毁
{
	free(php->a);
	php->size = 0;
	php->capacity = 0;
	php = NULL;
}

数值交换-Swap：

        这个函数是一个简单的交换函数，目的是为了便于下面的操作，下面的操作会用到多次交换，所以这里可以提前定义一个交换函数。

代码如下：

void Swap(HPDataType* a, HPDataType* b)		//交换函数
{
	HPDataType tem;
	tem = *a;
	*a = *b;
	*b = tem;
}

向上调整-AdjustUP：

        这个函数是为了下面的插入函数做准备，因为值插入在数组后可能使孩子大于父亲，数组不满足堆的性质，这时我们就需要向上调整。

代码如下：

//前提上面child部分是堆
void AdjustUP(HPDataType* a, int child)		//向上调整
{
	int parent = (child - 1) / 2;
	while (a[parent] < a[child])
	{
		Swap(&a[child], &a[parent]);
		child = parent;
		parent = (child - 1) / 2;
	}
}

插入-HeapPush：

        这里传入了结构体指针，该指针不能为空，故这里需要通过断言来增强代码的健壮性。除此之外，我们还需判断函数是否需要增容，若需要用realloc()函数增容即可。接着，直接插入即可，插入后，我们需要通过上面的AdjustUP()来判断是否需要进行向上调整。

代码如下：

void HeapPush(HP* php, HPDataType x)				//入堆
{
	assert(php);

	if (php->size == php->capacity)		//增容
	{
		HPDataType* tem= (HPDataType*)realloc(php->a,sizeof(HPDataType) * php->capacity*2);
		if (tem == NULL)
		{
			perror("realloc");
			return;
		}
		php->a = tem;
		php->capacity *= 2;
	}

	//插入
	php->a[php->size] = x;
	php->size++;

	//判断是否符合堆，是否需要调整。
	AdjustUP(php->a, php->size-1);
}

向下调整-AdjustDown：

        这个函数是为了下面的删除函数做准备，这里同上面向上调整原理相似，区别在于这里需要额外传入数组的大小来判断是否进行循环。

代码如下：

//前提 左右子树都是大堆或小堆
void AdjustDown(HPDataType* a, int n , int parent)		//向下调整
{
	int leftchild = parent * 2 + 1;
	int rightchild = parent* 2 + 2;
	int maxchild = 0;
	while (leftchild < n)
	{
		//选出左右孩子中最大的那个
		if (rightchild<n && a[rightchild]>a[leftchild])
		{
			maxchild = rightchild;
		}
		else
		{
			maxchild = leftchild;
		}

		if (a[maxchild] > a[parent])
		{
			Swap(&a[maxchild], &a[parent]);
            parent=maxcgild;
			leftchild = parent * 2 + 1;
			rightchild = parent* 2 + 2;
		}
		else
		{
			break;
		}
	}
}

删除-HeapPop：

        这里传入了结构体指针，该指针不能为空，故这里需要通过断言来增强代码的健壮性，另外，因为是删除所以我们还需断言一下是否堆空，这里我们删除堆顶方式是将堆顶元素与数组尾元素交换，然后删除为元素，接着进行向下调整使数组满足堆的性质。

代码如下：

void HeapPop(HP* php)				//删除
{
	assert(php);
	assert(!HeapEmpty(php));

	//删除数据
	Swap(&php->a[0], &php->a[php->size-1]);
	php->size--;
	//这时我们需要通过向下调整，来满足堆的定义
	AdjustDown(php->a, php->size, 0);
}

堆顶元素-HeapTop：

        这里传入了结构体指针，该指针不能为空，故这里需要通过断言来增强代码的健壮性。然后直接返回数组首元素值即是堆顶元素。

代码如下：

HPDataType HeapTop(HP* php)							//堆顶元素	
{
	assert(php);
	return php->a[0];
}

判空-HeapEmpty：

        这里传入了结构体指针，该指针不能为空，故这里需要通过断言来增强代码的健壮性。然后，直接通过结构体中size大小来判断是否堆空。

代码如下：

bool HeapEmpty(HP* php) 		//判空
{
	assert(php);
	return php->size == 0;
}

堆中元素个数-HeapSize：

        这里传入了结构体指针，该指针不能为空，故这里需要通过断言来增强代码的健壮性。然后直接返回结构体中size大小即可。

代码如下：

int HeapSize(HP* php)				//堆中元素个数
{
	assert(php);
	return php->size;
}

3.源文件-Test.c：

        对于源文件-Test.c，我们的目的是检测所定义的函数是否有问题，通过下面操作可初步判断。

代码及结果如下：

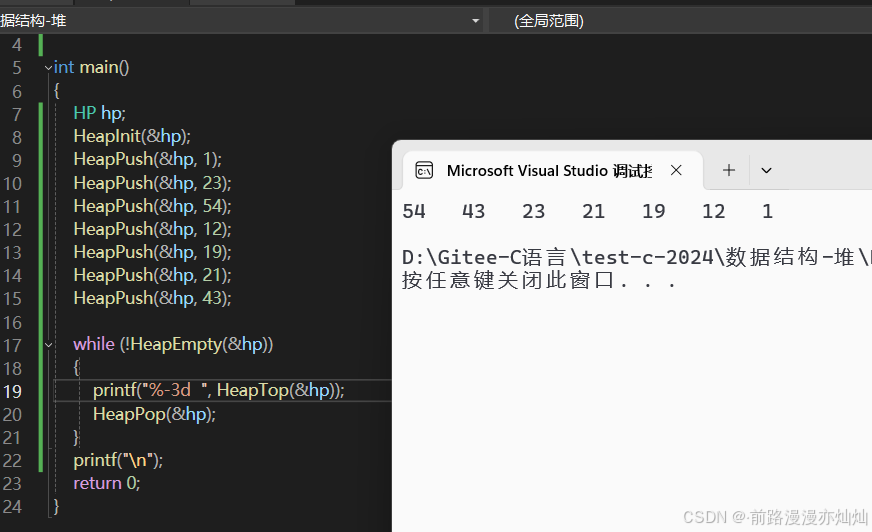
        通过上述产生的数组结果：54、43、23、21、19、12、1。我们可以判断最后输出的结果是否符合堆的性质。通过下面图片可知，显然数组结果符合堆的性质。

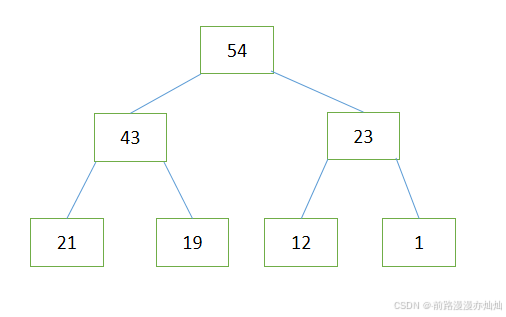
结语：

        上述内容，即是我个人对数据结构堆的基本操作的实现和见解。若有大佬发现哪里有问题可以私信或评论指教一下我这个小萌新。非常感谢各位友友们的点赞，关注，收藏与支持，我会更加努力的学习编程语言，还望各位多多关照，让我们一起进步吧！