Mad scientist Mike entertains himself by arranging rows of dominoes. He doesn't need dominoes, though: he uses rectangular magnets instead. Each magnet has two poles, positive (a "plus") and negative (a "minus"). If two magnets are put together at a close distance, then the like poles will repel each other and the opposite poles will attract each other.
Mike starts by laying one magnet horizontally on the table. During each following step Mike adds one more magnet horizontally to the right end of the row. Depending on how Mike puts the magnet on the table, it is either attracted to the previous one (forming a group of multiple magnets linked together) or repelled by it (then Mike lays this magnet at some distance to the right from the previous one). We assume that a sole magnet not linked to others forms a group of its own.

Mike arranged multiple magnets in a row. Determine the number of groups that the magnets formed.
The first line of the input contains an integer n (1 ≤ n ≤ 100000) — the number of magnets. Then n lines follow. The i-th line (1 ≤ i ≤ n) contains either characters "01", if Mike put the i-th magnet in the "plus-minus" position, or characters "10", if Mike put the magnet in the "minus-plus" position.
On the single line of the output print the number of groups of magnets.
6 10 10 10 01 10 10
3
4 01 01 10 10
2
The first testcase corresponds to the figure. The testcase has three groups consisting of three, one and two magnets.
The second testcase has two groups, each consisting of two magnets.
题目意思是说磁铁有正负极,同性相吸,异性相斥,现在用字符串01表示磁铁正负摆放,字符串10表示磁铁负正摆放,现在给定的n个磁铁依次放在一排,问总共可以组成多少组磁铁。由磁铁的特性可知,摆放方式相同的组成一组,所以当前摆放方式与前一个不同就表示一个磁铁组的开始,在开始的时候特判一下,就可以了。
代码如下:
/*************************************************************************
> File Name: a.cpp
> Author: gwq
> Mail: gwq5210@qq.com
> Created Time: 2014年11月13日 星期四 23时06分11秒
************************************************************************/
#include <cmath>
#include <ctime>
#include <cctype>
#include <climits>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <sstream>
#include <iostream>
#include <algorithm>
#define INF (INT_MAX / 10)
#define clr(arr, val) memset(arr, val, sizeof(arr))
#define pb push_back
#define sz(a) ((int)(a).size())
using namespace std;
typedef set<int> si;
typedef vector<int> vi;
typedef map<int, int> mii;
typedef long long ll;
const double esp = 1e-5;
int main(int argc, char *argv[])
{
int n;
while (scanf("%d", &n) != EOF) {
int ans = 0;
char s1[10], s2[10];
for (int i = 0; i < n; ++i) {
scanf("%s", s1);
if (i == 0 || strcmp(s1, s2) != 0) {
++ans;
}
strcpy(s2, s1);
}
printf("%d\n", ans);
}
return 0;
}Mad scientist Mike is busy carrying out experiments in chemistry. Today he will attempt to join three atoms into one molecule.
A molecule consists of atoms, with some pairs of atoms connected by atomic bonds. Each atom has a valence number — the number of bonds the atom must form with other atoms. An atom can form one or multiple bonds with any other atom, but it cannot form a bond with itself. The number of bonds of an atom in the molecule must be equal to its valence number.
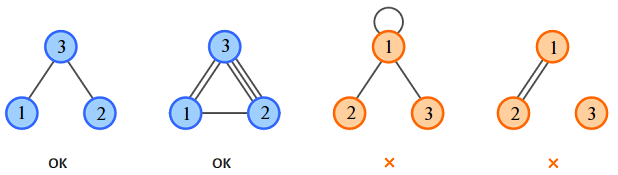
Mike knows valence numbers of the three atoms. Find a molecule that can be built from these atoms according to the stated rules, or determine that it is impossible.
The single line of the input contains three space-separated integers a, b and c (1 ≤ a, b, c ≤ 106) — the valence numbers of the given atoms.
If such a molecule can be built, print three space-separated integers — the number of bonds between the 1-st and the 2-nd, the 2-nd and the 3-rd, the 3-rd and the 1-st atoms, correspondingly. If there are multiple solutions, output any of them. If there is no solution, print "Impossible" (without the quotes).
1 1 2
0 1 1
3 4 5
1 3 2
4 1 1
Impossible
The first sample corresponds to the first figure. There are no bonds between atoms 1 and 2 in this case.
The second sample corresponds to the second figure. There is one or more bonds between each pair of atoms.
The third sample corresponds to the third figure. There is no solution, because an atom cannot form bonds with itself.
The configuration in the fourth figure is impossible as each atom must have at least one atomic bond.
代码如下:
/*************************************************************************
> File Name: b.cpp
> Author: gwq
> Mail: gwq5210@qq.com
> Created Time: 2014年11月13日 星期四 23时15分01秒
************************************************************************/
#include <cmath>
#include <ctime>
#include <cctype>
#include <climits>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <sstream>
#include <iostream>
#include <algorithm>
#define INF (INT_MAX / 10)
#define clr(arr, val) memset(arr, val, sizeof(arr))
#define pb push_back
#define sz(a) ((int)(a).size())
using namespace std;
typedef set<int> si;
typedef vector<int> vi;
typedef map<int, int> mii;
typedef long long ll;
const double esp = 1e-5;
int main(int argc, char *argv[])
{
int a, b, c;
while (scanf("%d%d%d", &a, &b, &c) != EOF) {
int tmp = a + b - c;
int x = tmp / 2;
int y = b - x;
int z = a - x;
//刚开始没判断tmp<0就会WA在tmp为-1时
if (tmp < 0 || (tmp % 2 == 1) || (x < 0) || (y < 0) || (z < 0)
|| (x == 0 && y == 0) || (x == 0 && z == 0)
|| (y == 0 && z == 0)) {
printf("Impossible\n");
} else {
printf("%d %d %d\n", x, y, z);
}
}
return 0;
}Mad scientist Mike is building a time machine in his spare time. To finish the work, he needs a resistor with a certain resistance value.
However, all Mike has is lots of identical resistors with unit resistance R0 = 1. Elements with other resistance can be constructed from these resistors. In this problem, we will consider the following as elements:
- one resistor;
- an element and one resistor plugged in sequence;
- an element and one resistor plugged in parallel.
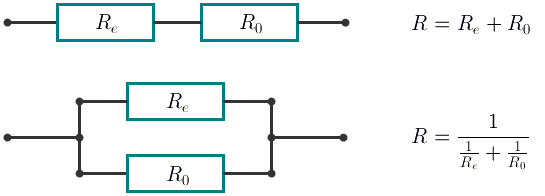
With the consecutive connection the resistance of the new element equals R = Re + R0.
With the parallel connection the resistance of the new element equals  .
In this case Re equals
the resistance of the element being connected.
.
In this case Re equals
the resistance of the element being connected.
Mike needs to assemble an element with a resistance equal to the fraction  .
Determine the smallest possible number of resistors he needs to make such an element.
.
Determine the smallest possible number of resistors he needs to make such an element.
The single input line contains two space-separated integers a and b (1 ≤ a, b ≤ 1018).
It is guaranteed that the fraction  is
irreducible. It is guaranteed that a solution always exists.
is
irreducible. It is guaranteed that a solution always exists.
Print a single number — the answer to the problem.
Please do not use the %lld specifier to read or write 64-bit integers in С++. It is recommended to use the cin, cout streams or the%I64d specifier.
1 1
1
3 2
3
199 200
200
In the first sample, one resistor is enough.
In the second sample one can connect the resistors in parallel, take the resulting element and connect it to a third resistor consecutively. Then, we get an element with resistance  .
We cannot make this element using two resistors.
.
We cannot make this element using two resistors.
物理中电阻的串联和并联,现在给定了一个电阻的值a/b,要求我们使用最少的电阻通过串联并联来得到这个电阻值,a/b是最简分数。我们只有电阻为1的单个电阻。题目保证答案存在。如果我们用k个电阻器得到了a/b的电阻,那么我们可以串联一个1的电阻器得到(a+b)/b的电阻,并联一个1的电阻器得到a/(a+b)的电阻,这个操作相当于更相减损法的一步逆推,更相减损法是每次大数减小数,所以最小的电阻数就是更相减损法的运算次数,因为开始只有1/1的电阻器,但是更相减损法效率太低,使用欧几里得算法求最大公约数的过程可以直接求出来更相减损法的步数。即每次ans加上b/a就可以了。
代码如下:
/*************************************************************************
> File Name: c.cpp
> Author: gwq
> Mail: gwq5210@qq.com
> Created Time: 2014年11月13日 星期四 23时50分00秒
************************************************************************/
#include <cmath>
#include <ctime>
#include <cctype>
#include <climits>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <sstream>
#include <iostream>
#include <algorithm>
#define INF (INT_MAX / 10)
#define clr(arr, val) memset(arr, val, sizeof(arr))
#define pb push_back
#define sz(a) ((int)(a).size())
using namespace std;
typedef set<int> si;
typedef vector<int> vi;
typedef map<int, int> mii;
typedef long long ll;
const double esp = 1e-5;
ll ans;
ll gcd(ll a, ll b)
{
if (a == 0) {
return b;
} else {
ans += b / a;
return gcd(b % a, a);
}
}
int main(int argc, char *argv[])
{
ll a, b;
while (cin >> a >> b) {
ans = 0;
gcd(a, b);
cout << ans << endl;
}
return 0;
}




 本文深入探讨了多种算法和技术的应用,包括数据结构、人工智能、区块链、云计算等领域的关键概念和实践案例,旨在帮助读者理解技术如何解决实际问题。
本文深入探讨了多种算法和技术的应用,包括数据结构、人工智能、区块链、云计算等领域的关键概念和实践案例,旨在帮助读者理解技术如何解决实际问题。
















 1121
1121

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








