切蛋糕

切蛋糕

Time Limit: 1000ms   Memory limit: 65536K  有疑问？点这里^_^

题目描述

现在有一块圆形大蛋糕。我们想知道切N刀最多能把蛋糕分成多少块。你能写个程序计算出么？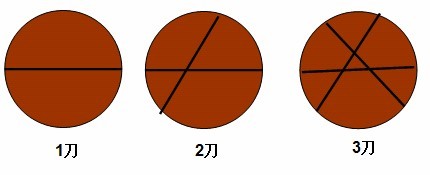

输入

 题目数据有多组，每组包含一个正整数N(1<=N<=100)。

输出

 对于每一组的N。输出N刀最多能把蛋糕切成多少块。

示例输入

123

示例输出

247

提示

 

来源

 

示例程序

 

#include<stdio.h>  
int main()  
{  
    int i,n,m;  
    while(scanf("%d",&n)!=EOF)  
    {  
        m=1;  
        for(i=1;i<=n;i++)  
        {  
            m+=i;  
        }  
        printf("%d\n",m);  
    }  
}