【剑指offer】剪绳子

【题目】给你一根长度为n的绳子，请把绳子剪成整数长的m段（m、n都是整数，n>1并且m>1），每段绳子的长度记为k[1],…,k[m]。请问k[1]x…xk[m]可能的最大乘积是多少？

例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

显然，可以尝试着将问题规模减小并挖掘不同规模问题间的关系。

思路一： 将f(n)转变为max(f(n-i)*i)问题，其中i为切分的那段长度为i

根据这个思路，可分别写出对应的递归方法、带备忘的递归方法以及DP方法。

• 暴力穷举，递归法

class Solution1:
    def cutRope(self, number):
        if number == 2:
            return 1
        if number == 3:
            return 2
        return self.cutRopeCore(number)

    def cutRopeCore(self, number):
        if number <= 3:
            return number

        maxProd = 1    # 初始值，假设全部为1，也可为0
        for i in range(1, number):
            maxProd = max(maxProd, i*self.cutRopeCore(number-i))

        return maxProd

该算法的时间复杂度O(n!) , 空间复杂度O(n)。

• 带备忘的递归法

显然，在上面的暴力穷举法中有很多重复的子问题计算，因此可以采用缓存机制将这些子问题的结果保存起来方便查询。

class Solution:
    def cutRope(self, number):
        if number == 2:
            return 1
        if number == 3:
            return 2
        cache = [-1] * (number+1)       # index=0为哨兵位
        return self.cutRopeCore(number, cache)

    def cutRopeCore(self, number, cache):
        if number <= 3:
            cache[number] = number
            return cache[number]

        for i in range(1, number+1):
            if cache[i] == -1:
                cache[i] = self.cutRopeCore(i, cache)
            cache[number] = max(cache[number], cache[i] * (number-i))

        return cache[number]

该算法的时间复杂度O(n^2)，空间复杂度O(n)。

• DP算法

参照上面的递归算法，我们从底向上就可以提出对应的DP算法，其中的状态变量为各子问题的最优解。

class Solution:
    def cutRope(self, number):
        if number == 2:
            return 1
        if number == 3:
            return 2

        # dps: 各长度的最优子长度乘积
        dps = [-1] * (number+1)       # index=0为哨兵位
        for i in range(1, number+1):
            if i <= 3:
                dps[i] = i
            else:
                for j in range(1, i):
                    dps[i] = max(dps[i], j*dps[i-j])

        return dps[-1]  return cache[number]

该算法的时间复杂度O(n^2)，空间复杂度O(n)

思路二：将f(n)转变为max(f(n-i)*f(i))，即两个最优子问题的乘积

在思路一中我们将子问题的规模不断-1，另一方面我们参考归并排序的想法，将子问题拆分为两个子问题的乘机。同样可以分别给出对应的归方法、带备忘的递归方法以及DP方法。

采用这种思路还有一个技巧，因为拆分子问题的对称性，所以在算法中只要考虑一般的搜索空间即可。

• 递归算法

class Solution:
    def cutRope(self, number):
        if number == 2:
            return 1
        if number == 3:
            return 2
        return self.cutRopeCore(number)

    def cutRopeCore(self, number):
        if number <= 3:
            return number

        maxProd = 1    # 初始值，假设全部为1，也可为0
        for i in range(1, number//2+1):       # 注意折半
            maxProd = max(maxProd, self.cutRopeCore(i)*self.cutRopeCore(number-i))

        return maxProd

• 带备忘的递归算法

class Solution2:
    def cutRope(self, number):
        if number == 2:
            return 1
        if number == 3:
            return 2
        cache = [-1] * (number+1)    # index=0为哨兵位
        return self.cutRopeCore(number, cache)

    def cutRopeCore(self, number, cache):
        if number <= 3:
            cache[number] = number
            return cache[number]

        for i in range(1, number//2+1):       # 注意折半, 注意+1
            if cache[i] == -1:
                cache[i] = self.cutRopeCore(i, cache)
            if cache[number-i] == -1:
                cache[number-1] = self.cutRopeCore(number-i, cache)
            cache[number] = max(cache[number], cache[i]*cache[number-i])

        return cache[number]

• DP算法

class Solution:
    def cutRope(self, number):
        if number == 2:
            return 1
        if number == 3:
            return 2

        dps = [-1] * (number+1)    # index=0为哨兵位
        for i in range(1, number+1):
            if i <= 3:
                dps[i] = i
            else:
                for j in range(1, i//2+1):
                    dps[i] = max(dps[i], dps[j]*dps[i-j])

        return dps[-1]

思路三：寻找f(n-1)和f(n)的直接关系

上面的两种思路都搜索了1～(n-1)规模的子问题，那么能否直接找到f(n-1)和f(n)间的关系呢？

假设我们现在对于f(n-1)已经有了最优的切分方案，那么当问题规模变为n时，我们该如何演变呢？此时，有三种选择：
（1）新增的1为新的一段，显然这种方案对于面积增加没有任何增益，因此舍弃；
（2）添加到一段上，显然添加到最短的一段对面积的增益越大；
（3）添加到一段并做重新拆分，此时又有了两个新问题：a) 添加到哪一段；b) 该段如何重新分割。这里不给证明的给出如下答案：选择最长的子段，分割为两段，且两段的距离尽可能相近。

由此可以给出对应的代码：

import math
class Solution:
    def cutRope(self, number):
        # write code here
        split_list = [1]
        for i in range(2, number + 1):
            minVal = min(split_list)
            maxVal = max(split_list)
            ratio_add_minVal = (minVal + 1) / minVal

            split_after_maxVal = int(math.sqrt(maxVal + 1))
            ratio_split_maxVal = (maxVal + 1 - split_after_maxVal) * split_after_maxVal / maxVal

            if ratio_split_maxVal >= ratio_add_minVal:
                split_list.remove(maxVal)
                split_list.extend([split_after_maxVal, maxVal + 1 - split_after_maxVal])

            else:
                split_list.remove(minVal)
                split_list.append(minVal + 1)

        prod = 1
        for i in split_list:
            prod *= i

        return prod

上述方案可以给出最优方案的各子段的情况，如
n=8, 对应的子段方案为[3, 2, 3]
n=15, 对应的子段方案为[3, 3, 3, 2, 2]
似乎各子段都是2和3的组合。

我们不妨从1开始，手动给出不限条件下各长度的最优解，确认里面的规律：
n=1, 不做分割 [1]
n=2, 不做分割 [2]
n=3, 不做分割 [3]
n=4, 分割为 [2, 2]
n=6, 分割为[2, 3]
n=7, 分割为 [2, 2, 3]
n = 8, 分割为 [2, 3, 3]
n = 9，分割为 [3, 3, 3]
…

不难看出，最优方案倾向于尽量分割为3的子段，但当最后一段为1时，需要和3重新组合起来（变成4）将其拆分为两个2。因此，我们可以给出下面的解决思路。

思路四：从数学上寻找关系

import math

class Solution:
    def cutRope(self, number):
        # write code here
        if number == 2:
            return 1
        if number == 3:
            return 2

        timesOf3 = number//3
        if number % 3 == 1:
            timesOf3 -= 1            # 若余数为1，与一个3凑成2*2

        timesOf2 = (number - timesOf3 * 3)//2

        return math.pow(3, timesOf3) * math.pow(2, timesOf2)

问题虽然解决了，为什么最优方案倾向于分裂为3的子段呢？根据Jesen不等式，将n分为k段，其乘积最大值当且仅当各段相等，且值为n/k时，此时乘积为(n/k)^k，可以给出不同k时的函数曲线如下：

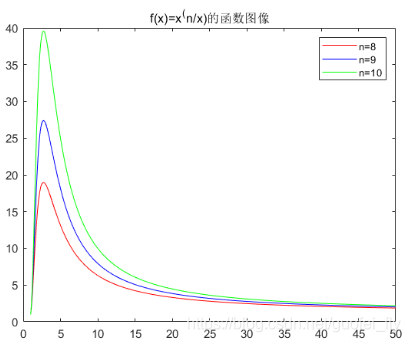
不难看到无论n为多少，其峰值均在3附近。

总结

1）如何将问题拆解为子问题，并建立联系是采用递归或DP类算法的核心。常见的包括-1规模，1～n-1规模，对半规模等。
2）注意边界条件和递归终止条件。
3）注意约束条件，如本题要求绳子必须切割，所以n=2、3时必须单独处理。但是在递归的子问题最优化中又需要考虑他们的最优解。这也是本题的一个坑。