SVM算法（九）将SVM推广到回归问题

如前文SVM算法的正则化损失函数视角中提及的，SVM可以理解为“广义线性损失函数+L2正则化”在损失函数为Hinge Loss下特例。即$$\min \frac{\lambda }{N}{w}^2+\frac{1}{N}\sum _{i=1}^{N}err(y_i,g(w{x}_i))$$式中$g(wx)$为线性函数。
本质上，SVM算法是基于二分类的最大软间隔分类算法，那如何将其推广到回归问题中呢？
有如下两种常见思路，其原则都是修改上述损失函数，使其适用于回归问题。

一、核岭回归(kernel ridge regression)

在线性回归(一)基础理论曾介绍过岭回归(即L2正则化的线性回归)：
$$\min \frac{\lambda }{N}{w}^2+\frac{1}{N}\sum _{i=1}^N(y_i-w{x}_i{)}^2$$又考虑到对于这种“广义线性损失函数+L2正则化”，线性参数$w$可以写成样本特征向量线性组合的形式，即：$$w^{\ast }=\sum _{j=1}^N{\beta }_j{x}_j$$将其代入岭回归目标函数，同时引入核技巧，可得$$\underset{\beta }{\min }\frac{\lambda }{N}\sum _{i=1}^N\sum _{j=1}^N{\beta }_i{\beta }_{j}K(x_i,x_j)+\frac{1}{N}\sum _{i=1}^N(y_i-\sum _{j=1}^N{\beta }_{j}K(x_i,x_j){)}^2$$写成向量形式，为：$$\underset{\mathbf{\beta }}{\min }\frac{\lambda }{N}{\mathbf{\beta }}^{\mathbf{T}}\mathbf{K}\mathbf{\beta }+\frac{1}{N}({\mathbf{\beta }}^{\mathbf{T}}{\mathbf{K}}^{\mathbf{T}}\mathbf{K}\mathbf{\beta }-2{\mathbf{\beta }}^{\mathbf{T}}{\mathbf{K}}^{\mathbf{T}}\mathbf{y}+{\mathbf{y}}^{\mathbf{T}}\mathbf{y})$$上式对$\mathbf{\beta }$求导，令其等于0，则可得极值点:$$\begin{array}{rl}{\nabla }_{\mathbf{\beta }}& =\frac{\lambda }{N}2{\mathbf{K}}^{\mathbf{T}}\mathbf{\beta }+\frac{1}{N}(2{\mathbf{K}}^{\mathbf{T}}\mathbf{K}\mathbf{\beta }-2{\mathbf{K}}^{\mathbf{T}}\mathbf{y})\\ & =\frac{2}{N}{\mathbf{K}}^{\mathbf{T}}((\mathbf{\lambda }\mathbf{I}+\mathbf{K})\mathbf{\beta }-\mathbf{y})\\ & =0\end{array}$$因为核函数矩阵$\mathbf{K}$为半正定阵（因为$K_{ij}=\varphi (x_i)\ast \varphi (y_i)$），而$\lambda <0$，因此$\mathbf{\lambda }\mathbf{I}+\mathbf{K}$必为正定阵，即可逆。所以$\mathbf{\beta }$存在解析的最优解：$${\mathbf{\beta }}^{\ast }=(\mathbf{\lambda }\mathbf{I}+\mathbf{K}{)}^{-1}\mathbf{y}$$本质上，核岭回归就是通过核技巧，将原始特征映射到高维非线性空间，再进行线性回归的过程。
从数学表达上，核岭回归通过将软间隔SVM目标函数的损失函数改写为MSE，因此也叫做最小回归SVM（least-squares SVM, 简称LSSVM）.

采用LSSVM的一种缺点在于其目标参数$\beta$的密集性。因为MSE对所有的预测值（只要预测值不等于真实值）都进行残差平方级的惩罚。所以，近乎所有的样本点都可视为支持向量，那么拉格朗日乘子$\beta$即非0。所以其计算量很大，而在标准的SVM算法中，参数$\alpha$是具备稀疏性的（即支持向量点占少数）。

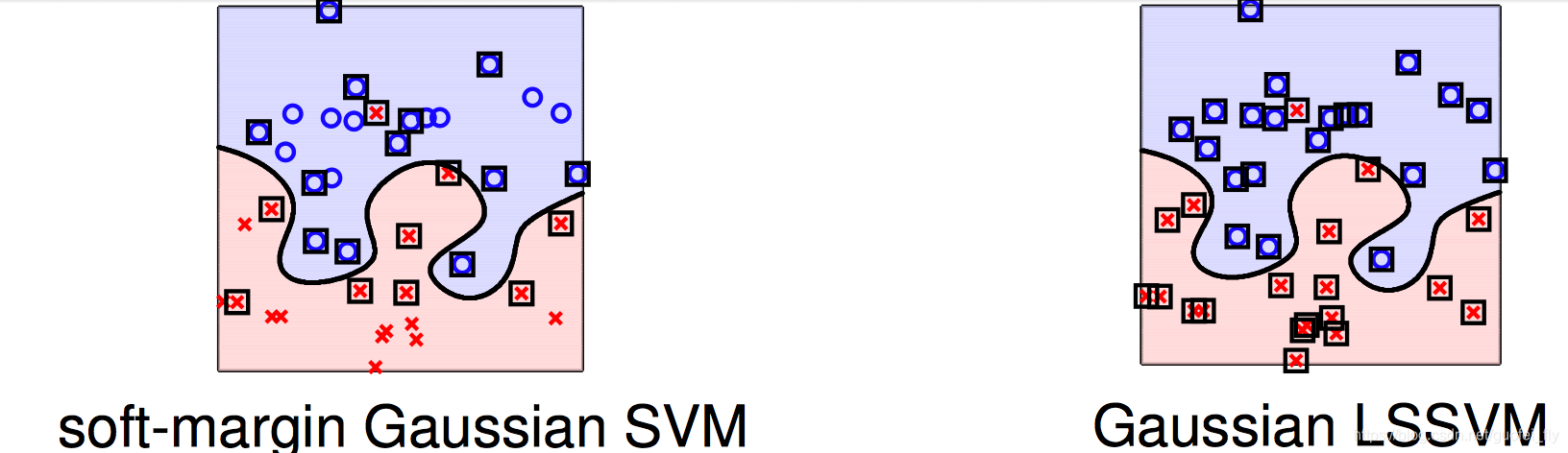
那么，有没有方法能够在进行做到像LSSVM一样解决回归问题，同时参数有具有稀疏性呢？答案同样是修改合适的损失函数。

二、Tube regression

从“广义线性损失函数+L2正则化”的视角来观察标准的SVM目标函数：$$\min \frac{\lambda }{N}{w}^2+\frac{1}{N}\sum _{i=1}^N\max (0,1-y_i(w{x}_i+b))$$通过构造Hinge损失函数，通过仅对$y_i(w{x}_i+b)\le 1$的样本点（即既非支持向量点，又非正确分类且间隔足够大的的那些点）进行惩罚。这是参数$\alpha$具有稀疏性的本质原因。

因此，可以在回归问题中，也构造具备类似性质的损失函数来取得类似的效果。定义tube损失函数：$$err(y,\hat{y})=\max (0,|y-\hat{y}|-ϵ),ϵ>0$$其中超参数$ϵ$可理解为对预测值偏差的容忍程度，在$ϵ$范围内可以不对误差值进行惩罚。当$ϵ=0$时，tube损失退化为MSE损失。从间隔的角度来看，tube损失相当于设置了一个单边宽度为$ϵ$的margin，margin外的误差才进行惩罚。

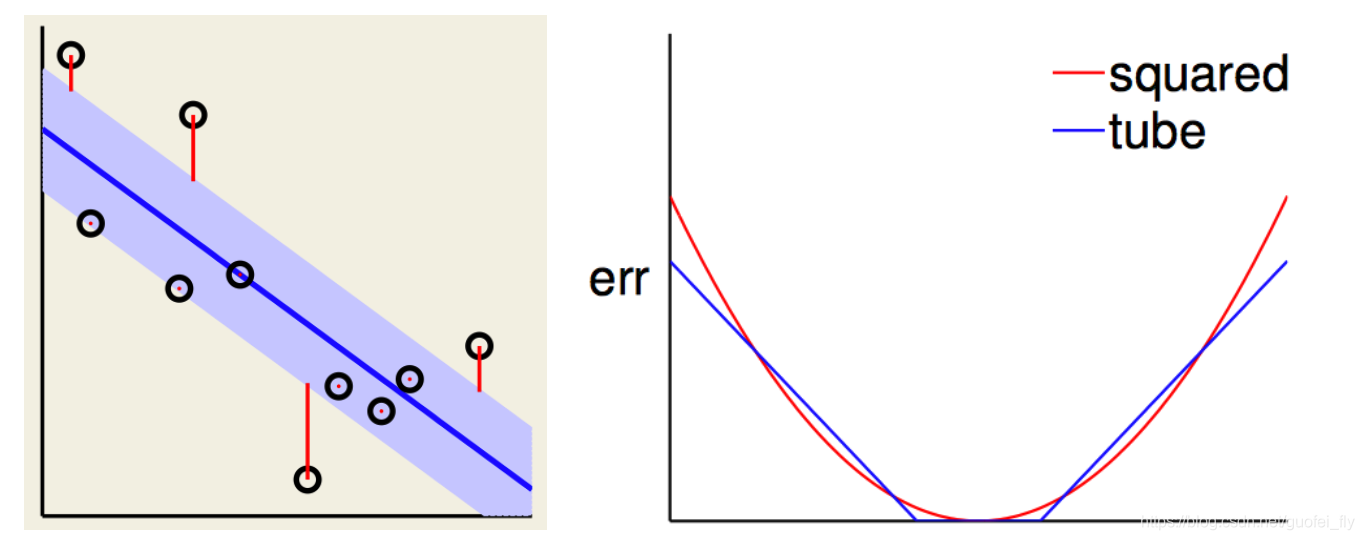
因此，在tube损失下的回归问题目标函数可写为：$$\min \frac{\lambda }{N}{w}^2+\frac{1}{N}\sum _{i=1}^N\max (0,|y-(wx+b)|-ϵ)$$虽然表达为“广义线性损失函数+L2正则化”的形式，优化目标无约束，但其不可微，并不方便求解。仿照在标准SVM问题中，“广义线性损失函数+L2正则化”与广义拉格朗日对偶问题的相互转化，可以尝试将其变为更易求解的二次规划问题。
注意到与标准SVM中惩罚项$1-y(wx+b)$不一样，这里的损失函数存在绝对值，因此需要同时对$y-(wx+b)$设置上界约束条件和下界约束函数，即写成：$$\begin{array}{rl}\underset{w,b,{ϵ}^{-},{ϵ}^{+}}{\min }& \frac{1}{2}{w}^2+C\sum _{i=1}^N({ϵ}_i^{+}+{ϵ}_i^{-})\\ s.t.& -ϵ-{ϵ}^{+}\le y_i-w{x}_i-b\le ϵ+{ϵ}^{+}\\ & {ϵ}^{+}\ge 0,{ϵ}^{-}\ge 0\end{array}$$上式中，$ϵ$为预设的超参数，而${ϵ}^{+},{ϵ}^{-}$分别为在$ϵ$基础上对上界约束和下界约束的进一步松弛。当然也能将两者合并进行统一表达。
类比于标准SVM中，将其表述为拉格朗日函数的极大极小问题，进而转化为对偶问题。通过求解拉格朗日乘子的二次规划问题，以及对偶补充条件，可以求得所有的参数，从而得到回归问题的解。