| 数据科学、数据分析、人工智能必备知识汇总-----机器学习-----XGBoost(Extreme Gradient Boosting,极端梯度集成)-----主目录-----持续更新:https://blog.youkuaiyun.com/grd_java/article/details/146939086 |
|---|
文章目录
- 1. 得出XGBoost最初的Obj目标函数
- 2. 推导XGBoost对Loss二阶泰勒展开之后的Obj
- 3. Obj化简常数项,明确训练每颗回归树需要准备的 g i g_i gi和 h i h_i hi
- 4. 重新定义树 f t f_t ft和树的复杂度 Ω \Omega Ω
- 5. 定义树的复杂度Define the Complexity of Tree
- 6. Revisit the Objectives 回顾目标函数
- 7. 推导XGBoost的Wj计算公式,推导评价树好坏的Obj
- 8. 根据Obj收益指导每一层分裂从而学习一棵树的结构
- 9. 从连续型和离散型变量中寻找最佳分裂条件
- 10. XGBoost中防止过拟合的前剪枝和后剪枝,学习率
- 11. 样本权重对于模型学习的影响
- 12. 总结XGBoost特性_包括缺失值的处理策略
1. 得出XGBoost最初的Obj目标函数
我们到底该怎么学呢?
Objective: ∑ i = 1 n l ( y i , y i ^ ) + ∑ k Ω ( f k ) , f k ∈ F \sum_{i=1}^n l(y_i,\hat{y_i})+\sum_k \Omega(f_k),f_k ∈ F ∑i=1nl(yi,yi^)+∑kΩ(fk),fk∈F
我们不能使用类似SGD(随机梯度下降法)的方法,去找到f(因为我们的函数空间的f,他们是一堆树,不是单纯的数值型的向量)
Solution解决方案:Additive Training累计训练(Boosting提升算法)
Additive Training是一种机器学习中的训练方法,主要用于提升树(Boosting)算法中,特别是在XGBoost等算法中应用广泛。其核心思想是在每一轮训练中,仅添加一个模型到当前的预测结果中,而不是重新训练整个模型。这种方法通过逐步优化预测结果来提高模型的准确性。
从constant prediction常数预测开始,每次添加一个new function 新的函数(决策树)
{ y i ^ ( 0 ) = 0 ,最初为常数 y i ^ ( 1 ) = f 1 ( x i ) = y i ^ ( 0 ) + f 1 ( x i ) ,之后每一轮都建立在上一轮结果之上,再加入本轮新的 f u n c t i o n ( 新的决策树 ) y i ^ ( 2 ) = f 1 ( x i ) + f 2 ( x i ) = y i ^ ( 1 ) + f 2 ( x i ) ⋯ y i ^ ( t ) = ∑ k = 1 t f k ( x i ) = y i ^ ( t − 1 ) + f t ( x i ) y i ^ ( t ) 为 t r a i n i n g − r o u n d − t (第 t 轮训练)的模型, y i ^ ( t − 1 ) 表示上一轮迭代出来的 f u n c t i o n 函数也要添加到本轮 f t ( x i ) 表示新的 f u n c t i o n 。 \begin{cases} \hat{y_i}^{(0)} = 0,最初为常数\\\\ \hat{y_i}^{(1)} = f_1(x_i)=\hat{y_i}^{(0)}+f_1(x_i),之后每一轮都建立在上一轮结果之上,再加入本轮新的function(新的决策树)\\\\ \hat{y_i}^{(2)} = f_1(x_i) + f_2(x_i)=\hat{y_i}^{(1)}+f_2(x_i)\\\\ \cdots \\\\ \hat{y_i}^{(t)} =\sum_{k=1}^t f_k(x_i)=\hat{y_i}^{(t-1)}+f_t(x_i)\\\\ \hat{y_i}^{(t)}为training-round-t(第t轮训练)的模型,\hat{y_i}^{(t-1)} 表示上一轮迭代出来的function函数也要添加到本轮\\\\ f_t(x_i)表示新的function。 \end{cases} ⎩ ⎨ ⎧yi^(0)=0,最初为常数yi^(1)=f1(xi)=yi^(0)+f1(xi),之后每一轮都建立在上一轮结果之上,再加入本轮新的function(新的决策树)yi^(2)=f1(xi)+f2(xi)=yi^(1)+f2(xi)⋯yi^(t)=∑k=1tfk(xi)=yi^(t−1)+ft(xi)yi^(t)为training−round−t(第t轮训练)的模型,yi^(t−1)表示上一轮迭代出来的function函数也要添加到本轮ft(xi)表示新的function。
注:y为已知常量
我们如何决定add添加哪个f(function,决策树)呢?
优化obj目标函数
在round t训练轮次t的预测是 y i ^ ( t ) = y i ^ ( t − 1 ) + f t ( x i ) \hat{y_i}^{(t)} =\hat{y_i}^{(t-1)}+f_t(x_i) yi^(t)=yi^(t−1)+ft(xi),其中 f t ( x i ) f_t(x_i) ft(xi)是我们在round t需要决定是否添加的f,也是我们在第t轮学习出来的树。
{ O b j ( t ) = ∑ i = 1 n l ( y i , y i ^ ( t ) ) + ∑ i = 1 t Ω ( f i ) = 展开可得 ∑ i = 1 n l ( y i , y i ^ ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) + c o n s t a n t ( 常数 ) 其中 ∑ i = 1 n l ( y i , y i ^ ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) 的目标是找到 f t 将其最小化, l 是 l o s s 的缩写。 ( G o a l : f i n d f t t o m i n i m i z e t h i s ) Ω ( f t ) 是第 t 轮的复杂度,前面 t − 1 个时刻训练出来的树已经不会变了,因此复杂度也不变,所以 c o n s t a n t ( 常数 ) 表示前面 t − 1 棵树的复杂度。在不断求导最小化目标函数过程中,和常数没关系(常数导数为 0 )。 \begin{cases} Obj^{(t)} &=\sum_{i=1}^n l(y_i,\hat{y_i}^{(t)}) + \sum_{i=1}^t \Omega(f_i) \\\\ &\stackrel{展开可得}{=} \sum_{i=1}^n l\Big(y_i,\hat{y_i}^{(t-1)}+f_t(x_i)\Big) + \Omega(f_t) + constant (常数)\\\\ &其中\sum_{i=1}^n l\Big(y_i,\hat{y_i}^{(t-1)}+f_t(x_i)\Big) + \Omega(f_t)的目标是找到f_t将其最小化,l是loss的缩写。(Goal: find \space\space f_t \space\space to\space\space minimize \space\space this)\\\\ &\Omega(f_t)是第t轮的复杂度,前面t-1个时刻训练出来的树已经不会变了,因此复杂度也不变,所以\\\\ &constant (常数)表示前面t-1棵树的复杂度。在不断求导最小化目标函数过程中,和常数没关系(常数导数为0)。 \end{cases} ⎩ ⎨ ⎧Obj(t)=∑i=1nl(yi,yi^(t))+∑i=1tΩ(fi)=展开可得∑i=1nl(yi,yi^(t−1)+ft(xi))+Ω(ft)+constant(常数)其中∑i=1nl(yi,yi^(t−1)+ft(xi))+Ω(ft)的目标是找到ft将其最小化,l是loss的缩写。(Goal:find ft to minimize this)Ω(ft)是第t轮的复杂度,前面t−1个时刻训练出来的树已经不会变了,因此复杂度也不变,所以constant(常数)表示前面t−1棵树的复杂度。在不断求导最小化目标函数过程中,和常数没关系(常数导数为0)。
可以回忆一下square loss,真实的 y i y_i yi减去预测的 y i ^ = y i ^ ( t − 1 ) + f t ( x i ) \hat{y_i}=\hat{y_i}^{(t-1)} + f_t(x_i) yi^=yi^(t−1)+ft(xi)
{ O b j ( t ) = ∑ i = 1 n ( y i − ( y i ^ ( t − 1 ) + f t ( x i ) ) ) 2 + Ω ( f t ) + c o n s t = ∑ i = 1 n [ 2 ( y i ^ ( t − 1 ) − y i ) f t ( x i ) + f t ( x i ) 2 ] + Ω ( f t ) + c o n s t 其中 2 ( y i ^ ( t − 1 ) − y i ) 通常在上一轮称为 r e s i d u a l 剩余、残差,第二个式子是第一个式子完全平方公式展开出来的, 但是展开后,需要将 y i 和 y i ^ ( t − 1 ) 看成常数,因为他们在第 t 轮次是不变的,将其统一扔给最后面的 c o n s t 里面 \begin{cases} Obj^{(t)} &=\sum_{i=1}^n \Big({ y_i - ( \hat{y_i}^{(t-1)} + f_t(x_i) ) }\Big)^2 + \Omega(f_t) + const\\\\ &=\sum_{i=1}^n \Big[ 2(\hat{y_i}^{(t-1)}-y_i)f_t(x_i) + f_t(x_i)^2 \Big] + \Omega(f_t) + const\\\\ &其中2(\hat{y_i}^{(t-1)}-y_i)通常在上一轮称为residual剩余、残差,第二个式子是第一个式子完全平方公式展开出来的,\\\\ &但是展开后,需要将y_i和\hat{y_i}^{(t-1)}看成常数,因为他们在第t轮次是不变的,将其统一扔给最后面的const里面 \end{cases} ⎩ ⎨ ⎧Obj(t)=∑i=1n(yi−(yi^(t−1)+ft(xi)))2+Ω(ft)+const=∑i=1n[2(yi^(t−1)−yi)ft(xi)+ft(xi)2]+Ω(ft)+const其中2(yi^(t−1)−yi)通常在上一轮称为residual剩余、残差,第二个式子是第一个式子完全平方公式展开出来的,但是展开后,需要将yi和yi^(t−1)看成常数,因为他们在第t轮次是不变的,将其统一扔给最后面的const里面
2. 推导XGBoost对Loss二阶泰勒展开之后的Obj
Taylor Expansion Approximation of Loss(Loss的泰勒展开近似)
Goal: O b j ( t ) = ∑ i = 1 n l ( y i , y i ^ ( t − 1 ) + f t ( x i ) ) + Ω ( f t ) + c o n s t a n t Obj^{(t)} = \sum_{i=1}^nl\Big(y_i,\hat{y_i}^{(t-1)}+f_t(x_i)\Big)+\Omega(f_t)+constant Obj(t)=∑i=1nl(yi,yi^(t−1)+ft(xi))+Ω(ft)+constant
seems still complicated except for the case of square loss:除了平方损失的情况外,似乎仍然很复杂。意思是说上一节我们化简出来的这个公式,还是太复杂啦,除非把 l l l损失函数替换为square loss
对Obj进行泰勒展开
Recall回想泰勒公式: f ( x ) = f ( x 0 ) + f ′ ( x 0 ) 1 ! ⋅ ( x − x 0 ) 1 + f ′ ′ ( x 0 ) 2 ! ⋅ ( x − x 0 ) 2 + f ′ ′ ′ ( x 0 ) 3 ! ⋅ ( x − x 0 ) 3 + . . . + f n ( x 0 ) n ! ⋅ ( x − x 0 ) n + R N ( 余项 O ( ( x − x 0 ) n ) ) f(x) = f(x_0)+\dfrac{f^{'}({x_0})}{1!}·(x-x_0)^1+\dfrac{f^{''}({x_0})}{2!}·(x-x_0)^2+\dfrac{f^{'''}({x_0})}{3!}·(x-x_0)^3+...+\dfrac{f^{n}({x_0})}{n!}·(x-x_0)^n + RN(余项O((x-x^0)^n)) f(x)=f(x0)+1!f′(x0)⋅(x−x0)1+2!f′′(x0)⋅(x−x0)2+3!f′′′(x0)⋅(x−x0)3+...+n!fn(x0)⋅(x−x0)n+RN(余项O((x−x0)n))。
我们并不需要这么复杂,我们只需要展开到二阶,也就是 f ( x + Δ x ) ⋍ f ( x ) + f ′ ( x ) Δ x + f ′ ′ ( x ) Δ x 2 2 f(x+\Delta x)\backsimeq f(x)+f^{'}(x)\Delta x + \dfrac{f^{''}(x)\Delta x^2}{2} f(x+Δx)⋍f(x)+f′(x)Δx+2f′′(x)Δx2,其中 Δ x \Delta x Δx是 x − x 0 x-x_0 x−x0。注意这里面的 f f f其实是我们目标函数中的 l l l,损失函数。同时我们是在 x x x这一点展开,所以 x x x不是变量,而 Δ x \Delta x Δx是变量,对应目标函数中的 f t ( x i ) f_t(x_i) ft(xi)。
Define 定义 对 y ^ ( t − 1 ) 的一阶偏导 g i = ∂ y ^ ( t − 1 ) l ( y i , y ^ ( t − 1 ) ) , 二阶偏导 h i = ∂ y ^ ( t − 1 ) 2 l ( y i , y ^ ( t − 1 ) ) 对\hat{y}^{(t-1)}的一阶偏导g_i = \partial_{\hat{y}^{(t-1)}}l(y_i,\hat{y}^{(t-1)}),二阶偏导h_i=\partial_{\hat{y}^{(t-1)}}^2l(y_i,\hat{y}^{(t-1)}) 对y^(t−1)的一阶偏导gi=∂y^(t−1)l(yi,y^(t−1)),二阶偏导hi=∂y^(t−1)2l(yi,y^(t−1))
g i 中的 g 表示 g_i中的g表示 gi中的g表示gradient梯度, h i 中的 h 表示 h_i中的h表示 hi中的h表示hessian矩阵。同时注意是将损失函数 l l l做二阶泰勒展开。
O b j ( t ) ⋍ ∑ i = 1 n [ l ( y i , y i ^ ( t − 1 ) ) + g i f t ( x i ) + h i f t 2 ( x i ) 2 ] + Ω ( f t ) + c o n s t a n t Obj^{(t)} \backsimeq \sum_{i=1}^n \Big[ {l(y_i,\hat{y_i}^{(t-1)})+ g_if_t(x_i) + \dfrac{h_i f_t^2(x_i)}{2} \Big] +\Omega(f_t) + constant} Obj(t)⋍∑i=1n[l(yi,yi^(t−1))+gift(xi)+2hift2(xi)]+Ω(ft)+constant,
最终目标函数就变成了这样(这个式子要记住),再次提醒,是对损失函数二阶泰勒展开,不是对目标函数本身。
如果你对上面这个式子感觉精神不适,想想square loss。就是说,你要是觉得上面的 g g g和 h h h很别扭的话,将里面的损失函数 l l l换成square loss再尝试理解一下
g i = ∂ y ^ ( t − 1 ) ( y ^ ( t − 1 ) − y i ) 2 = 2 ( y ^ ( t − 1 ) − y i ) , h i = ∂ y ^ ( t − 1 ) 2 ( y i − y ^ ( t − 1 ) ) 2 = 2 g_i = \partial_{\hat{y}^{(t-1)}} (\hat{y}^{(t-1)} - y_i)^2 = 2(\hat{y}^{(t-1)}-y_i),h_i = \partial_{\hat{y}^{(t-1)}}^2(y_i - \hat{y}^{(t-1)})^2 = 2 gi=∂y^(t−1)(y^(t−1)−yi)2=2(y^(t−1)−yi),hi=∂y^(t−1)2(yi−y^(t−1))2=2
将我们得到的内容与上一个公式进行比较,发现用square loss求一阶偏导,和JBDT的负梯度拟合残差很相似,也就是一阶泰勒展开。而XGBoost是二阶泰勒展开,上面的 h i h_i hi就是求的二阶导数,自然比JBDT更加优秀。
3. Obj化简常数项,明确训练每颗回归树需要准备的 g i g_i gi和 h i h_i hi
此时我们有了新的目标函数,就是上一节中近似出来的 O b j ( t ) ⋍ ∑ i = 1 n [ l ( y i , y i ^ ( t − 1 ) ) + g i f t ( x i ) + h i f t 2 ( x i ) 2 ] + Ω ( f t ) + c o n s t a n t Obj^{(t)} \backsimeq \sum_{i=1}^n \Big[ {l(y_i,\hat{y_i}^{(t-1)})+ g_if_t(x_i) + \dfrac{h_i f_t^2(x_i)}{2} \Big] +\Omega(f_t) + constant} Obj(t)⋍∑i=1n[l(yi,yi^(t−1))+gift(xi)+2hift2(xi)]+Ω(ft)+constant,给他简化一下
你要明确,t-1时刻的 l ( y i , y i ^ ( t − 1 ) ) l(y_i,\hat{y_i}^{(t-1)}) l(yi,yi^(t−1))已经确定了(前面t-1颗的小树,已经训练完固定下来的,不会变了),所以这在t轮迭代中,也是常数项。最终剩下的变量只有 f ( t ) f(t) f(t)了。
目标函数,去除常数项,一阶项用 g i g_i gi表达,二阶项用 h i h_i hi表达。这就是新的目标函数,我们要使得Obj尽可能小,和常数项没有关系,要研究的是 f t f_t ft为何值时,使得整体最小。因此最终化简成以下形式,n条样本代入进去加和,但是过程中去除常数项。
∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) \sum_{i=1}^n [ g_i f_t(x_i) + \dfrac{1}{2} h_i f_t^2(x_i)]+\Omega (f_t) ∑i=1n[gift(xi)+21hift2(xi)]+Ω(ft),其中 g i = ∂ y ^ ( t − 1 ) l ( y i , y ^ ( t − 1 ) ) g_i = \partial_{\hat{y}(t-1)} l(y_i,\hat{y}^{(t-1)}) gi=∂y^(t−1)l(yi,y^(t−1)), h i = ∂ y ^ ( t − 1 ) 2 l ( y i , y ^ ( t − 1 ) ) h_i=\partial_{\hat{y}^{(t-1)}}^2l(y_i,\hat{y}^{(t-1)}) hi=∂y^(t−1)2l(yi,y^(t−1))
明确一下: g i g_i gi是上一时刻t-1的loss,对上一时刻t-1的 y ^ ( t − 1 ) \hat{y}^{(t-1)} y^(t−1)进行求导。我们在t时刻求 f t f_t ft时,上一时刻t-1的东西是已知的。所以 g i g_i gi和 h i h_i hi都是可以求出来的。也就是说,JBDT每次训练要准备负梯度,而XGBoost我们要每次都准备 g i g_i gi和 h i h_i hi
Why spending much efforts to derive the objective, why not just grow trees… 为什么我们花费这么多精力推导目标函数,去聊的这么深入,就种树不行吗(直接训练)…
Theoretical benefit 理论效益,理论上的优势:能明确我们到底在学什么,convergence收敛,汇聚融合(让函数收敛,让Obj最小)
Engineering benefit 工程效益:回顾一下有监督学习的要素,结合起来进行理解
g i g_i gi和 h i h_i hi 是从definition of loss function 损失函数的定义中来的。
对于function(就是一颗颗小决策树)的学习(求解每个时刻点的 f f f),仅仅依靠于通过 g i g_i gi和 h i h_i hi(需要我们自己准备)定义的目标函数Obj就可以做到
想一想你如何能在被要求实现square loss(做回归) 和 logistic loss(做分类)的boosted tree增强树时,将代码模块分开(就是一套代码,既可以做回归又可以做分类)。
4. 重新定义树 f t f_t ft和树的复杂度 Ω \Omega Ω
refine the definition of tree。改善树的定义
我们通过在叶子结点中的a vector of scores分数向量去定义树,当然还有一个(同样是定义树的)叶子节点的索引映射函数,将一个叶子的实例(说白了就是样本),映射到一个叶子结点。
就是说,我们每一颗小树,都会学习到一个树的结构,此时给我们一条样本数据,代入到树中,最终会落到一个对应的叶子结点L中。而为什么是落到叶子结点L而不是X呢?就是通过索引映射函数来实现。
f t ( x ) = w q ( x ) , w ∈ R T , R T 是树的叶子 w e i g h t 权重, q : R d → { 1 , 2 , ⋯ , T } f_t(x) = w_{q(x)},w ∈ \R^T,\R^T是树的叶子weight权重,q:\R^d \rightarrow \{ 1,2,\cdots,T \} ft(x)=wq(x),w∈RT,RT是树的叶子weight权重,q:Rd→{1,2,⋯,T},q是树结构,就是一个样本进来落到哪个叶子结点
此时我们的 f t f_t ft就完成了重新定义,以后 w q ( x ) w_{q(x)} wq(x)就是它的全新定义形式,而它本身代表的就是 f t f_t ft的过程。x代入到 f t ( x ) f_t(x) ft(x)的计算过程就是 w q ( x ) w_{q(x)} wq(x),表示先代入 q ( x ) q(x) q(x)得到它落入哪个叶子结点,根据叶子结点的索引号,得到叶子结点的weight权重。
5. 定义树的复杂度Define the Complexity of Tree
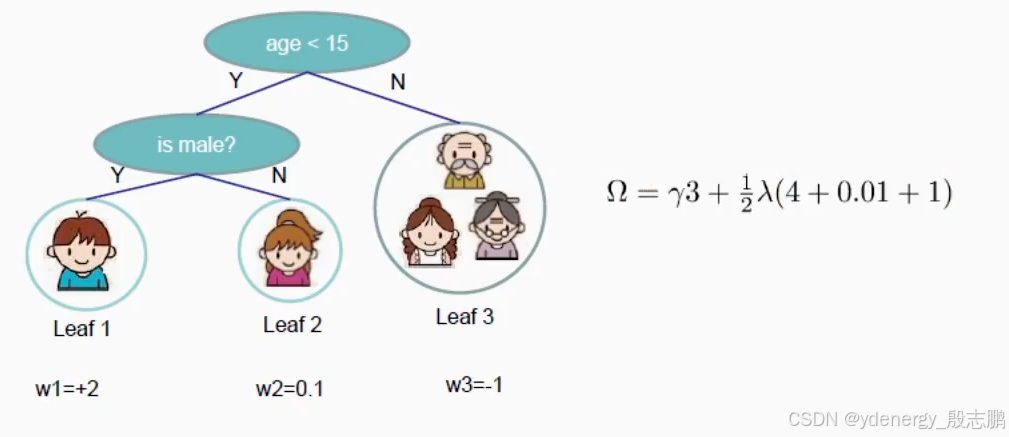
Define complexity as 定义复杂度为(this is not the only possible definition这不是唯一可能的定义形式) Ω ( f t ) = γ T + 1 2 λ ∑ j = 1 T w j 2 \Omega (f_t) = \gamma T + \dfrac{1}{2} \lambda \sum_{j=1}^T w_j^2 Ω(ft)=γT+21λ∑j=1Twj2
其中 γ T \gamma T γT中 T T T为Number of leaves 叶子的数量( γ \gamma γ是个超参数,是未来我们建立模型需要指定的参数), w j w_j wj是第 j j j个叶子结点的分数, 1 2 λ ∑ j = 1 T w j 2 \dfrac{1}{2} \lambda \sum_{j=1}^T w_j^2 21λ∑j=1Twj2是L2 norm of leaf scores 叶子分值的L2范式(L2正则项)。
从公式可以看出,树的结构简单了,那么 γ T \gamma T γT就会越少,复杂度就越低。 w j w_j wj越小,惩罚项 1 2 λ ∑ j = 1 T w j 2 \dfrac{1}{2} \lambda \sum_{j=1}^T w_j^2 21λ∑j=1Twj2也就越小。相应的泛化能力也就越强。
6. Revisit the Objectives 回顾目标函数
上面重新定义了小树和复杂度,我们用到目标函数中,就可以得到一个全新的目标函数(越来越接近XGBoost的核心函数了,上面推导那么多,就是为了从我们已有的简单知识,推导到XGBoost的核心,理解每一部分是怎么来的)
Define the instance set in leaf j j j (将叶子 j j j里面定义的样本集实例) as 定义为 I j = { i ∣ q ( x i ) = j } I_j = \{ i| q(x_i) = j \} Ij={i∣q(xi)=j}
I j I_j Ij就是第j个instance实例(样本)
q ( x i ) q(x_i) q(xi)就是将第i条样本代入到我们的query里面去(就是上面讲的索引映射函数,代入样本最终落到哪个叶子结点中)
j j j表示第j个叶子结点,也就是代入到索引映射函数中,最终落到的那个叶子结点。而落到第j个叶子结点的条件 q ( x i ) q(x_i) q(xi)所对应的样本就是 i i i,最终的样本实例就是 I j I_j Ij
Regroup the objective by each leaf 通过每个叶子结点(进行加和)重组目标函数。我们之前对 O b j Obj Obj引入了 g g g和 h h h,之后将 f t ( x i ) f_t(x_i) ft(xi)换成了 w q ( x i ) w_{q(x_i)} wq(xi),重新定义了复杂度 Ω ( f t ) = γ T + 1 2 λ ∑ j = 1 T w j 2 \Omega (f_t) = \gamma T + \dfrac{1}{2} \lambda \sum_{j=1}^T w_j^2 Ω(ft)=γT+21λ∑j=1Twj2,依次代入并化简。
{ O b j ( t ) ⋍ ∑ i = 1 n [ g i f t ( x i ) + 1 2 h i f t 2 ( x i ) ] + Ω ( f t ) = ∑ i = 1 n [ g i w q ( x i ) + 1 2 h i w q ( x i ) 2 ] + γ T + λ 1 2 ∑ j = 1 T w j 2 ,然后我们将前面的部分也改成对 T 进行加和 = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T \begin{cases} Obj^{(t)} & \backsimeq \sum_{i=1}^n [g_i f_t(x_i) + \dfrac{1}{2}h_i f_t^2(x_i)] + \Omega(f_t)\\\\ & = \sum_{i=1}^{\textcolor{red}{n}} [g_i w_{q(x_i)} + \dfrac{1}{2} h_i w_{q(x_i)}^2] + \gamma T + \lambda \dfrac{1}{2}\sum_{j=1}^T w_j^2,然后我们将前面的部分也改成对T进行加和\\\\ & = \sum_{j=1}^{\textcolor{blue}{T}} [(\sum_{i ∈ I_j}g_i)w_j + \dfrac{1}{2}(\sum_{i ∈ I_j} h_i + \lambda)w_j^2] + \gamma T \end{cases} ⎩ ⎨ ⎧Obj(t)⋍∑i=1n[gift(xi)+21hift2(xi)]+Ω(ft)=∑i=1n[giwq(xi)+21hiwq(xi)2]+γT+λ21∑j=1Twj2,然后我们将前面的部分也改成对T进行加和=∑j=1T[(∑i∈Ijgi)wj+21(∑i∈Ijhi+λ)wj2]+γT
其中,为什么1到n条样本的加和可以换成1到T个叶子结点的数量进行加和呢?
没有树结构时,相要将所有样本相关的值进行集成(加和),就可以对1到n条样本代入函数进行加和。
而有了树结构,每个样本最终都会落到一个叶子结点里面去,将每个叶子结点中落入的样本单独进行聚合,然后对这些在叶子结点中"部分聚合"完成的值,进行 T T T次"全局聚合"即可。
g i g_i gi是第 i i i条样本求一阶偏导的梯度值, w q ( x i ) w_{q(x_i)} wq(xi)表示第 i i i条样本 x i x_i xi落入第t棵小树中最终给出的分值(假设落入第 j j j个叶子结点,那么对应给出的分值就是 w j w_j wj, w j w_j wj是第 j j j个叶子结点的分数)。此时可以将 w j w_j wj里面所有的样本的 g i g_i gi加在一起 ∑ i ∈ I j g i \sum_{i ∈ I_j}g_i ∑i∈Ijgi,然后直接乘以 w j w_j wj即可,因为落入第j个叶子结点的样本,最终给出的分值都是 w j w_j wj
本质上,假设1,2,3这3条样本都落入第j个叶子结点,那么代入 g i w q ( x i ) g_i w_{q(x_i)} giwq(xi)再加和到一起,由于 g i g_i gi不一样所以需要单独求,而他们落入第j个叶子结点的 w q ( x i ) w_{q(x_i)} wq(xi)对应的分值都一样是 w j w_j wj
∑ i ∈ I j g i \sum_{i ∈ I_j}g_i ∑i∈Ijgi, i ∈ I j i ∈I_j i∈Ij表示 i i i是第j个叶子结点里面的样本
同理 ∑ i = 1 n 1 2 h i w q ( x i ) 2 \sum_{i=1}^{\textcolor{red}{n}}\dfrac{1}{2} h_i w_{q(x_i)}^2 ∑i=1n21hiwq(xi)2可以变为 ∑ i = 1 T [ 1 2 ( ∑ i ∈ I j h i w j 2 ] \sum_{i=1}^T [ \dfrac{1}{2}(\sum_{i ∈ I_j} h_iw_j^2] ∑i=1T[21(∑i∈Ijhiwj2],此时公式后面的复杂度里面还有一个 λ 1 2 ∑ j = 1 T w j 2 \lambda \dfrac{1}{2}\sum_{j=1}^T w_j^2 λ21∑j=1Twj2,哥俩放到一起变成 ∑ i = 1 T 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 \sum_{i=1}^T\dfrac{1}{2}(\sum_{i ∈ I_j} h_i + \lambda)w_j^2 ∑i=1T21(∑i∈Ijhi+λ)wj2
This is sum of T independent quadratic functions 这是T个独立二次函数的和
7. 推导XGBoost的Wj计算公式,推导评价树好坏的Obj
The Structure Score. 结构得分。
Two facts about single variable quadratic function. 关于单变量二次函数的两个事实。就是两个公式,记住就行。
arg min x G x + 1 2 H x 2 = − G H , H > 0 。 min x G x + 1 2 H x 2 = − 1 2 G 2 H \argmin_{x} Gx + \dfrac{1}{2}H x^2 = -\dfrac{G}{H},H>0。\min_x Gx + \dfrac{1}{2} H x^2 = -\dfrac{1}{2}\dfrac{G^2}{H} argminxGx+21Hx2=−HG,H>0。minxGx+21Hx2=−21HG2
arg min x \argmin_x argminx表示当 x x x为多少时,其限制的函数 G x + 1 2 H x 2 Gx + \dfrac{1}{2}H x^2 Gx+21Hx2为最小(找其一阶导为0的点,为最值,限定二次项系数H大于0,则为凹函数,一阶导数为0点必是最小值,最终算出来就是 x 为 − G H x为-\dfrac{G}{H} x为−HG时函数取最小值)。
将 x = − G H x=-\dfrac{G}{H} x=−HG代入 G x + 1 2 H x 2 Gx + \dfrac{1}{2}H x^2 Gx+21Hx2就可以求出函数的最小值 − 1 2 G 2 H -\dfrac{1}{2}\dfrac{G^2}{H} −21HG2, min x \min_x minx表示其限定函数的最小值,因此 min x G x + 1 2 H x 2 = − 1 2 G 2 H \min_x Gx + \dfrac{1}{2} H x^2 = -\dfrac{1}{2}\dfrac{G^2}{H} minxGx+21Hx2=−21HG2
设 G j = ∑ i ∈ I j g i G_j = \sum_{i ∈ I_j}g_i Gj=∑i∈Ijgi , H j = ∑ i ∈ I j h i H_j = \sum_{i ∈ I_j} h_i Hj=∑i∈Ijhi
{ O b j ( t ) = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T = ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T ,此时就化简为了 arg min x G x + 1 2 H x 2 = − G H , H > 0 的形式 λ 和 γ 是超参数都是已知的,如果树的结构定下来了,那么 g i 和 h i 也已知,对应的就可以求出 G 和 H 。 T 是叶子结点数量,也是已知。 最终未知的只有 w j 是多少。 \begin{cases} Obj^{(t)} &= \sum_{j=1}^T [(\sum_{i ∈ I_j}g_i)w_j + \dfrac{1}{2}(\sum_{i ∈ I_j} h_i + \lambda)w_j^2] + \gamma T\\\\ &= \sum_{j=1}^T[G_jw_j + \dfrac{1}{2}(H_j + \lambda)w_j^2]+\gamma T,此时就化简为了\argmin_{x} Gx + \dfrac{1}{2}H x^2 = -\dfrac{G}{H},H>0的形式\\\\ & \lambda 和 \gamma 是超参数都是已知的,如果树的结构定下来了,那么g_i和h_i也已知,对应的就可以求出G和H。T是叶子结点数量,也是已知。\\\\ &最终未知的只有w_j是多少。 \end{cases} ⎩ ⎨ ⎧Obj(t)=∑j=1T[(∑i∈Ijgi)wj+21(∑i∈Ijhi+λ)wj2]+γT=∑j=1T[Gjwj+21(Hj+λ)wj2]+γT,此时就化简为了argminxGx+21Hx2=−HG,H>0的形式λ和γ是超参数都是已知的,如果树的结构定下来了,那么gi和hi也已知,对应的就可以求出G和H。T是叶子结点数量,也是已知。最终未知的只有wj是多少。
Assume the structure of tree ( q ( x ) q(x) q(x)) is fixed, the optimal weight in each leaf, and the resulting objective value are假设树的结构( q ( x ) q(x) q(x))是固定的(就是第t时刻的一颗树已经训练出来了),每个叶子的最佳权重和最终的目标值为(就是套个公式,叶子结点的权重为多少时,损失 [ G j w j + 1 2 ( H j + λ ) w j 2 ] [G_jw_j + \dfrac{1}{2}(H_j + \lambda)w_j^2] [Gjwj+21(Hj+λ)wj2]为最小,也就是最优解 w j ∗ w^*_j wj∗,树最优的分值。然后带回到目标函数中的 w j w_j wj里面,拿到Obj在t时刻的最小值 m i n w [ G j w j + 1 2 ( H j + λ ) w j 2 ] min_w [G_jw_j + \dfrac{1}{2}(H_j + \lambda)w_j^2] minw[Gjwj+21(Hj+λ)wj2]):
w j ∗ = − G j H j + λ w^*_j = -\dfrac{G_j}{H_j + \lambda} wj∗=−Hj+λGj, O b j = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T Obj = -\dfrac{1}{2}\sum_{j=1}^T \dfrac{G_j^2}{H_j + \lambda}+\gamma T Obj=−21∑j=1THj+λGj2+γT
此时有了 O b j = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T Obj = -\dfrac{1}{2}\sum_{j=1}^T \dfrac{G_j^2}{H_j + \lambda}+\gamma T Obj=−21∑j=1THj+λGj2+γT,就可以拿到它对应优化的最小损失,来评判我们的树结构有多好。如果我们的树可以将损失尽可能减小,那树结构自然也表示更优秀。这样就可以方便我们评判哪棵树更加优秀。
8. 根据Obj收益指导每一层分裂从而学习一棵树的结构
目前我们的 O b j ( t ) Obj^{(t)} Obj(t)变成了 ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T \sum_{j=1}^{\textcolor{blue}{T}} [(\sum_{i ∈ I_j}g_i)w_j + \dfrac{1}{2}(\sum_{i ∈ I_j} h_i + \lambda)w_j^2] + \gamma T ∑j=1T[(∑i∈Ijgi)wj+21(∑i∈Ijhi+λ)wj2]+γT,其中 T T T是叶子结点的数量
同时我们将其化简为 ∑ j = 1 T [ G j w j + 1 2 ( H j + λ ) w j 2 ] + γ T ,化简为了 arg min x G x + 1 2 H x 2 = − G H , H > 0 的形式 \sum_{j=1}^T[G_jw_j + \dfrac{1}{2}(H_j + \lambda)w_j^2]+\gamma T,化简为了\argmin_{x} Gx + \dfrac{1}{2}H x^2 = -\dfrac{G}{H},H>0的形式 ∑j=1T[Gjwj+21(Hj+λ)wj2]+γT,化简为了argminxGx+21Hx2=−HG,H>0的形式
通过两个公式 arg min x G x + 1 2 H x 2 = − G H , H > 0 。 min x G x + 1 2 H x 2 = − 1 2 G 2 H \argmin_{x} Gx + \dfrac{1}{2}H x^2 = -\dfrac{G}{H},H>0。\min_x Gx + \dfrac{1}{2} H x^2 = -\dfrac{1}{2}\dfrac{G^2}{H} argminxGx+21Hx2=−HG,H>0。minxGx+21Hx2=−21HG2
我们有了最优解(第j个叶子结点分值) w j ∗ = − G j H j + λ w^*_j = -\dfrac{G_j}{H_j + \lambda} wj∗=−Hj+λGj, 对应优化的最小损失 O b j = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T Obj = -\dfrac{1}{2}\sum_{j=1}^T \dfrac{G_j^2}{H_j + \lambda}+\gamma T Obj=−21∑j=1THj+λGj2+γT
The Structure Score Calculation 树结构分值的计算
在我们算第t棵树的时候,实际上每条样本早已准备好了 g g g和 h h h
对 y ^ ( t − 1 ) 的一阶偏导 g i = ∂ y ^ ( t − 1 ) l ( y i , y ^ ( t − 1 ) ) , 二阶偏导 h i = ∂ y ^ ( t − 1 ) 2 l ( y i , y ^ ( t − 1 ) ) 对\hat{y}^{(t-1)}的一阶偏导g_i = \partial_{\hat{y}^{(t-1)}}l(y_i,\hat{y}^{(t-1)}),二阶偏导h_i=\partial_{\hat{y}^{(t-1)}}^2l(y_i,\hat{y}^{(t-1)}) 对y^(t−1)的一阶偏导gi=∂y^(t−1)l(yi,y^(t−1)),二阶偏导hi=∂y^(t−1)2l(yi,y^(t−1))
上图中有5条样本,以及第t棵树结构,这颗树有3个叶子结点,第一个叶子结点有一个样本 { 1 } \{1\} {1},对应的 G 1 = g 1 G_1=g_1 G1=g1, H 1 = h 1 H_1=h_1 H1=h1。第二个叶子结点包含样本 { 4 } \{4\} {4}。第三个叶子结点包含3条样本 { 2 , 3 , 5 } \{2,3,5\} {2,3,5},对应的 G 3 = g 2 + g 3 + g 5 G_3=g_2+g_3+g_5 G3=g2+g3+g5和 H 3 = h 2 + h 3 + h 5 H_3=h_2+h_3+h_5 H3=h2+h3+h5都是将每条样本的 g g g和 h h h进行加和
因此,我们有了每个叶子结点的 G G G和 H H H,就可以计算对应优化的最小损失 O b j = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T Obj = -\dfrac{1}{2}\sum_{j=1}^T \dfrac{G_j^2}{H_j + \lambda}+\gamma T Obj=−21∑j=1THj+λGj2+γT
T T T是叶子结点的数量为3, λ \lambda λ是超参数,我们可以先省略 1 2 \dfrac{1}{2} 21,最终就有了图中的 O b j = − ∑ j G j 2 H j + λ + 3 γ Obj = -\sum_j \dfrac{G_j^2}{H_j+\lambda}+3\gamma Obj=−∑jHj+λGj2+3γ,这个分数越小(损失小),这颗树的结构就越好。
Searching Algorithm for Single Tree对单颗树的搜索算法,前面的推导都是建立在已有第t棵树的情况下,那么如何寻找到 f t f_t ft呢?
1. 枚举可能的树结构 q q q,并不是一个可能的事情,不太现实,尤其是特征多的情况下,可能性太多了。
2. 计算q的结构分值,通过我们前面计算分值的公式 O b j = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T Obj = -\dfrac{1}{2}\sum_{j=1}^T \dfrac{G_j^2}{H_j + \lambda}+\gamma T Obj=−21∑j=1THj+λGj2+γT
3. 找到最好的树结构,并且使用最佳的叶子结点权重optimal leaf weight。有了树结构后,可以通过最优解 w j ∗ = − G j H j + λ w^*_j = -\dfrac{G_j}{H_j + \lambda} wj∗=−Hj+λGj算出第j个叶子结点分值
4. 但…这里可能有无穷多种可能的树结构,这个方案只是很理想的一种情况,实际去实现,是不现实的。
Greedy Learning of the Tree 树的贪婪学习,贪婪算法思想,从根结点开始,每一层分裂都判断分裂还是不分裂。
In practice, we grow the tree greedily。在实践中,我们贪婪地(贪婪学习,不是疯狂种树的意思)种树
从树的depth 0根结点开始
对树的每个叶子结点,尝试去add a split分裂(添加一个分支,就是分裂一次,和GBDT一样基于CART,都是二叉树)。添加分支后,obj的改变为(也就是说,每次分裂,我们都重新计算分裂后的obj分值,以此来判断我们该不该进行这次分裂。每增加一个分支,树结构就会更复杂,因此相对的,我们要让这次分裂能够增加树预测的准确率,而不是分裂后,复杂度增加了但没什么收益)
G a i n = G L 2 H L + λ + G R 2 H R + λ − ( G L + G R ) 2 H L + H R + λ − γ Gain = \dfrac{G_L^2}{H_L+\lambda} + \dfrac{G_R^2}{H_R+\lambda} - \dfrac{(G_L + G_R)^2}{H_L + H_R + \lambda} - \gamma Gain=HL+λGL2+HR+λGR2−HL+HR+λ(GL+GR)2−γ:分裂前的分值 − ( G L + G R ) 2 H L + H R + λ - \dfrac{(G_L + G_R)^2}{H_L + H_R + \lambda} −HL+HR+λ(GL+GR)2,减去,分裂后的分值,额外减去复杂度,称为Gain收益(这个式子看起来像分裂后的分值减去了分裂前,仔细看下面的推导,这个式子是如何推算出来的)。这里依旧省略了 1 2 \dfrac{1}{2} 21
− G L 2 H L + λ -\dfrac{G_L^2}{H_L+\lambda} −HL+λGL2是(分裂一个)左孩子后的obj分值, G L G_L GL是当前要分裂的父结点所有分到左孩子样本的 g g g加和, H L H_L HL同理。 L L L是left的缩写,代表左孩子。
− G R 2 H R + λ -\dfrac{G_R^2}{H_R+\lambda} −HR+λGR2是右孩子的分值
− ( G L + G R ) 2 H L + H R + λ -\dfrac{(G_L + G_R)^2}{H_L + H_R + \lambda} −HL+HR+λ(GL+GR)2是如果我们不split分裂的分值(就是我们分裂之前的obj分值),首先,如果父结点x分裂,有了左右孩子(一定为叶子结点),那么本来应该落入x结点的样本都会落入到左右孩子中,所以 G L + G R G_L + G_R GL+GR就是分裂之前父结点x的 G G G, H L + H R H_L + H_R HL+HR同理
γ \gamma γ是The complexity cost by introducing additional leaf 引入额外叶子的复杂性成本,是一个大于0的超参数,因此Gain收益计算时,是减去这个超参数,代表对这次分裂的惩罚(因为复杂度增加了)
最后,分裂前的分值 − ( G L + G R ) 2 H L + H R + λ -\dfrac{(G_L + G_R)^2}{H_L + H_R + \lambda} −HL+HR+λ(GL+GR)2减去分裂后的分值就是 − ( G L + G R ) 2 H L + H R + λ − ( − G L 2 H L + λ ) − ( − G R 2 H R + λ ) -\dfrac{(G_L + G_R)^2}{H_L + H_R + \lambda}-(-\dfrac{G_L^2}{H_L+\lambda})-(-\dfrac{G_R^2}{H_R+\lambda}) −HL+HR+λ(GL+GR)2−(−HL+λGL2)−(−HR+λGR2),负负得正,把正的放前面就是 G L 2 H L + λ + G R 2 H R + λ − ( G L + G R ) 2 H L + H R + λ \dfrac{G_L^2}{H_L+\lambda} + \dfrac{G_R^2}{H_R+\lambda} - \dfrac{(G_L + G_R)^2}{H_L + H_R + \lambda} HL+λGL2+HR+λGR2−HL+HR+λ(GL+GR)2
剩下的问题是:我们如何找到the best split最好的分裂。(一般来讲分裂之前的obj-分裂之后的obj应该是一个大于0的数,代表整体损失减少了。)
每次分裂都计算Gain收益,收益就是Obj分值,Obj就是损失。哪一个特征可以使得我们这次分裂的时候,整体的损失减少的更多,那么这次就用这个条件进行分裂。
因此,XGBoost,是使用Obj来作为分裂指标的。
9. 从连续型和离散型变量中寻找最佳分裂条件
Efficient Finding of the Best Split 高效找到最佳的分割(分裂)
什么是一个分裂规则split rule x j < a x_j < a xj<a的gain收益?假设 x j x_j xj是age年龄这个维度(连续型的数据特征),如何选择最佳的分裂。下图中,首先从左到右,从最年轻到最年老进行排序。每个分裂点计算很简单,相邻两个的分值加起来求均值,例如小女孩和妈妈之间进行分裂,假设小女孩age为10,妈妈为30,那么 10 + 30 = 40 , 40 / 2 = 20 10+30=40,40/2=20 10+30=40,40/2=20,因此图中竖线a此时就是20。左边的样本就会落入左节点,右边的会落入右节点。
我们只需要将每边的 g g g和 h h h进行加和,然后计算 G a i n = G L 2 H L + λ + G R 2 H R + λ − ( G L + G R ) 2 H L + H R + λ − γ Gain = \dfrac{G_L^2}{H_L+\lambda} + \dfrac{G_R^2}{H_R+\lambda} - \dfrac{(G_L + G_R)^2}{H_L + H_R + \lambda} - \gamma Gain=HL+λGL2+HR+λGR2−HL+HR+λ(GL+GR)2−γ。
对排序实例进行从左到右的线性扫描就足以确定沿特征的最佳分割(上图中一共有4个可选的分裂点,从左到右线性的扫描,依次是小男孩和小女孩中间,已经在上图使用的a分裂点,妈妈和奶奶中间,奶奶和爷爷中间。分别计算Gain然后比较即可)
An Algorithm for Split Finding 一种分割查找算法
对于每个node节点,枚举所有features特征
对每个feature特征,对instances样本实例(如果是连续型的)通过特征值排序(不是连续型的也能排序,只不过受限制)
使用线性扫描决定对应特征的最佳分裂条件
在所有特征中选取最佳的分裂解决方案(对每个特征找出最佳的分裂,算出收益,不同的特征再进行比较,得到哪一个特征对应的分裂指标是最佳的分裂条件)
生成一颗K层的树的Time Complexity时间复杂度(需要数据结构和算法的知识,参考快速排序和二叉树的时间复杂度)
O ( n ∗ d ∗ K ∗ log 2 n ) O(n*d*K*\log_2 n) O(n∗d∗K∗log2n):每个层级,需要 O ( n ∗ log 2 n ) O(n*\log_2 n) O(n∗log2n)时间复杂度去排序。一共有 d d d个特征需要排序,并且我们需要在每层(树深,一共 K K K层)都去做这件事,因此时间复杂度为 O ( n ∗ d ∗ K ∗ log 2 n ) O(n*d*K*\log_2 n) O(n∗d∗K∗log2n)
是可以被特征优化的,例如使用近似approximation 或者 caching the sorted features缓存已排序的特征(回溯算法思想,对重复的操作进行缓存,例如上一次需要对d个纬度进行排序,这次还需要再次使用这个操作,那么上一次就可以将结果进行缓存,这次直接查缓存就行)。
可以扩展到非常大的数据集,一般来讲,树模型都可以适应特别大的数据集。
What about Categorical Variables?对于离散型(分类)的变量呢?(例如性别,男和女这种就是离散型特征)
一些树学习算法会分别地处理离散型变量和连续型变量
我们可以轻松使用我们的评分公式(前面介绍的计算Gain的公式)去评价,需不需要对基于某个离散型变量特征去进行分裂。
实际上,分别处理离散并不是必须的(只是针对XGBoost,在XGBoost中,没有必要单独处理离散型数据)。
我们可以将离散型变量进行One-Hot编码,将其编码为numerical vector数字矢量(向量)。例如性别有男和女,则可以编辑为(0,1)代表女,(1,0)代表男。第一条样本如果是女,那么起编码为(0,1)
z j = { 1 如果 x 属于类别 j 0 o t h e r w i s e 其它类别 z_j = \begin{cases} 1 & 如果 x 属于 类别 j\\\\0 &otherwise其它类别 \end{cases} zj=⎩ ⎨ ⎧10如果x属于类别jotherwise其它类别
编码完成后,我们的数据会变的非常稀疏,树模型的学习算法(XGBoost和GBDT)是非常喜欢去处理这类数据的。
10. XGBoost中防止过拟合的前剪枝和后剪枝,学习率
Pruning and Regularization剪枝和正则
回顾分裂收益公式 G a i n = G L 2 H L + λ + G R 2 H R + λ − ( G L + G R ) 2 H L + H R + λ − γ Gain = \dfrac{G_L^2}{H_L+\lambda} + \dfrac{G_R^2}{H_R+\lambda} - \dfrac{(G_L + G_R)^2}{H_L + H_R + \lambda} - \gamma Gain=HL+λGL2+HR+λGR2−HL+HR+λ(GL+GR)2−γ,这个收益他可以是负数!
当the training loss reduction训练损失降幅 G L 2 H L + λ + G R 2 H R + λ − ( G L + G R ) 2 H L + H R + λ \dfrac{G_L^2}{H_L+\lambda} + \dfrac{G_R^2}{H_R+\lambda} - \dfrac{(G_L + G_R)^2}{H_L + H_R + \lambda} HL+λGL2+HR+λGR2−HL+HR+λ(GL+GR)2 比 regularization正则项惩罚系数 γ \gamma γ小的时候
Trade-off权衡 simplicity简单(复杂度低,方差低) 和 predictivness预测性(泛化能力强,精度高,误差低)
所以说,我们每次训练树结构时,都会考虑正则项和泛化能力,包括计算叶子分值时也会考虑 λ \lambda λ
Pre-stopping提前终止(前剪枝)
Stop split if the best split have negative gain.若最佳分裂是负收益则停止分裂
But maybe a split can benefit future splits… 但是也可能一个分裂(当前是负收益)可以在未来的分裂(之后继续分裂的话)中获得更大收益(整体,分裂完成后当前分子算上所有的负收益和正收益,整体是正收益)。相当于前面投资了一下,产生负收益,之后都是大额利润正收益。
Post-Prunning(后剪枝)
Grow a tree to maximum depth(最大深度,超参数), recursively prune all the leaf splits with negative gain.将树生长到最大深度,并递归地剪除所有增益为负的叶子节点。
Recap: Boosted Tree Algorithm.回顾:Boosted Tree(提升树)算法
Add a new tree in each Iterator.在每轮迭代(每次循环)中添加一棵新树。
Beginning of each iteration,calculate每次迭代开始时,进行计算
g i = ∂ y ˆ ( t − 1 ) l ( y i , y ˆ ( t − 1 ) ) g_i = \partial_{\^{y}^{(t-1)}}l(y_i,\^{y}^{(t-1)}) gi=∂yˆ(t−1)l(yi,yˆ(t−1)), h i = ∂ y ˆ ( t − 1 ) 2 l ( y i , y ˆ ( t − 1 ) ) h_i = \partial^2_{\^{y}^{(t-1)}} l(y_i,\^y^{(t-1)}) hi=∂yˆ(t−1)2l(yi,yˆ(t−1))
Use the statistics to greedily grow a tree利用统计数据贪婪地构建一棵树 f t ( x ) f_t(x) ft(x),(根据每次的Obj的收益,来算每次分裂,然后通过下面的公式算每个叶子分值)
O b j = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T Obj = -\dfrac{1}{2} \displaystyle \sum_{j=1}^T \dfrac{G_j^2}{H_j+\lambda}+\gamma T Obj=−21j=1∑THj+λGj2+γT,(计算分值的公式)
Add f t ( x ) f_t(x) ft(x) to the model y ˆ i ( t ) = y ˆ i ( t − 1 ) + f t ( x i ) \^y_i^{(t)} = \^y_i^{(t-1)} + f_t(x_i) yˆi(t)=yˆi(t−1)+ft(xi),生成的树 f t ( x ) f_t(x) ft(x),加到整体的模型中去 y ˆ i ( t ) = y ˆ i ( t − 1 ) + f t ( x i ) \^y_i^{(t)} = \^y_i^{(t-1)} + f_t(x_i) yˆi(t)=yˆi(t−1)+ft(xi)。
Usually, instead we do y ( t ) = y ( t − 1 ) + ϵ f t ( x i ) y^{(t)} = y^{(t-1)} + \epsilon f_t(x_i) y(t)=y(t−1)+ϵft(xi),通常,作为替代的,我们会乘一个 ϵ \epsilon ϵ然后加到整体的强学习器中去。
ϵ \epsilon ϵ is called step-size(步长) or shrinkage(收缩量,说白了就是学习率), usually set around 0.1 0.1 0.1通常设置在0.1左右
This means we do not do full optimization in each step and reserve chance for future rounds, it helps prevent overfitting.意味着我们在每次迭代生成这颗树并不完全去做优化,我们去给后面的轮次保留一些机会(给后面留更多的学习空间),帮我们防止过拟合。
11. 样本权重对于模型学习的影响
How can we build a boosted tree classifier to do weighted regression problem, such that each instance have a importance weight?我们如何构建一个提升树分类器(这个分类器每个实例都有一个实例权重)来解决加权回归问题?
Define objective定义目标函数,calculate计算 g i , h i g_i,h_i gi,hi,feed it to the old tree learning algorithm we have for un-weighted version把它输入到我们为无权重版本设计的老树学习算法中(训练损失中,我们会在每条样本的损失前面乘上sample weight简单权重).
最小二乘训练损失没条样本损失前乘 a i a_i ai(就是sample weight) l ( y i , y ˆ i ) = 1 2 a i ( y ˆ i − y i ) 2 l(y_i,\^y_i) = \dfrac{1}{2} a_i(\^y_i - y_i)^2 l(yi,yˆi)=21ai(yˆi−yi)2。这条样本的loss的一阶导数也需要前面乘 a i a_i ai, g i = a i ( y ˆ i − y i ) g_i = a_i(\^y_i - y_i) gi=ai(yˆi−yi)。此时二阶导 h i = a i h_i = a_i hi=ai
Again think of separation of model and objective, how does the theory can help better organizing the machine learning toolkit.再次考虑模型与目标的分离,理论如何帮助更好地组织机器学习工具集?
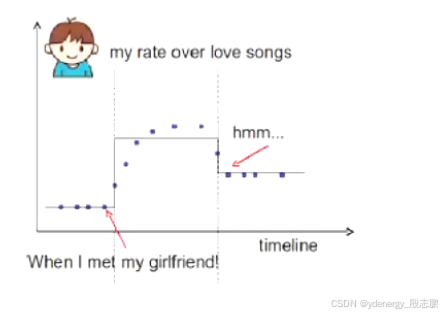
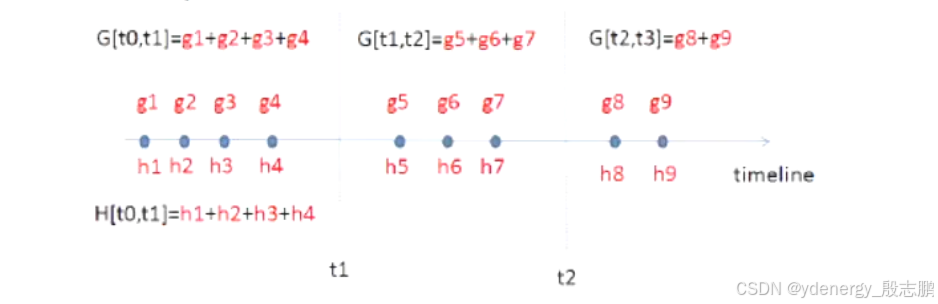
Back to the time series problem, if I want to learn step functions over time. Is there other ways to learn the time splits, other than the top down split approach?回到时间序列问题(下图中x轴是时间),如果我想学习随时间变化的阶梯函数(就是下图中的线去拟合散点),除了自上而下的分割方法外,还有其他方法可以学习时间分割吗?
时间序列问题
All that is important is the structure score of the splits。分裂与否,最重要的还是结构分数(怎么分裂,分数最高)
O b j = − 1 2 ∑ j = 1 T G j 2 H j + λ + γ T Obj = -\dfrac{1}{2} \displaystyle \sum_{j=1}^T \dfrac{G_j^2}{H_j+\lambda}+\gamma T Obj=−21j=1∑THj+λGj2+γT,(计算分值的公式)
Top-down greedy,same as trees.像树一样从上到下做贪婪分裂。
Bottom-up greedy, start from individual points as each group, greedily merge neighbors.贪心地自下而上的,从每个单独的点作为一组开始,贪心地合并相邻的点。
Dynamic programming, can find optimal solution for this case.动态规划,也可以找到这种情况下的最佳分裂。
总结
The separation between model, objective, parameters can be helpful for us to understand and customize leaning models.模型、目标、参数之间的分离有助于我们理解和定制学习模型(自定义loss时,要保证一阶( g i g_i gi)和二阶可导( h i h_i hi))。
The bias-variance trade-off applies everywhere, including learning in functional space 偏差-方差权衡无处不在,包括在函数空间中的学习也一样需要用到
O b j ( Θ ) = L ( Θ ) + Ω ( Θ ) Obj(\Theta) = L(\Theta) + \Omega(\Theta) Obj(Θ)=L(Θ)+Ω(Θ)目标函数=损失loss函数+复杂度
We can be formal about what we learn and how we learn. Clear understanding of theory can be used to guide cleaner implementation.我们可以对我们所学的内容以及学习方式保持正式的态度。因为对理论的清晰理解可以用来引导更简洁的实现
12. 总结XGBoost特性_包括缺失值的处理策略
1.传统的GBDT以CART树作为基学习器,XGBoost还支持线性分类器,这个时候XGBoost相当于L1和L2正则化的逻辑斯蒂回归(分类)或者线性回归(回归);(相当于将逻辑回归和线性回归串联到一起做Boosting,同时会考虑正则项)
2.传统的GBDT在优化的时候只用到一阶导数信息,XGBoost则对代价函数(Obj)进行了二阶泰勒展开,得到一阶( g i g_i gi)和二阶导数( h i h_i hi);对比GBDT,loss下降更快。
3.XGBoost在代价函数中加入了正则项,用于控制模型的复杂度。从权衡方差偏差来看,它降低了模型的方差,使学习出来的模型更加简单,防止过拟合,这也是XGBoost优于传统GBDT的一个特性;主要针对单颗树防止过拟合。
4.shrinkage(缩减),相当于学习速率(XGBoost中的eta)。XGBoost在进行完一次迭代时,会将叶子节点的权值乘上该系数,主要是为了削弱每棵树的影响,让后面有更大的学习空间。(GBDT也有学习速率);也可以防止过拟合(对整体强学习器)。
5.列抽样。XGBoost借鉴了随机森林的做法,支持列抽样,不仅防止过拟合,还能减少计算;这里对应一些超参数,主要有两个,subsample,colsample_bytree
6.对缺失值的处理(XGBoost自动会做)。对于特征的值有缺失的样本,XGBoost还可以自动学习出它的分裂方向;通常情况下,我们人为在处理缺失值的时候大多会选用中位数、均值或是二者的融合来对数值型特征进行填补,使用出现次数最多的类别来填补缺失的类别特征。在逻辑实现上,为了保证完备性,会分别处理将missing(缺失)该特征值的样本分配到左叶子结点和右叶子结点的两种情形,计算增益后选择增益大的方向进行分裂即可(就是说,如果一个特征值为None空值,也会成为分裂条件)。可以为缺失值或者指定的值指定分支的默认方向,这能大大提升算法的效率。如果在训练中没有缺失值而在预测中出现缺失(例如通过用电量和发电量预测电价,实际预测中没有用电量数据,此时用电量特征值就是缺失值),那么会自动将缺失值的划分方向放到右子树。
7.XGBoost工具支持并行。Boosting不是一种串行的结构吗?怎么并行的?注意XGBoost的并行不是tree粒度的并行,XGBoost也是一次迭代完才能进行下一次迭代的(第t次迭代的代价函数里包含了前面t-1次迭代的预测值)。XGBoost的并行是在特征粒度上的。我们知道,决策树的学习最耗时的一个步骤就是对特征的值进行排序(因为要确定最佳分割点),XGBoost在训练之前,预先对数据进行了排序,然后保存为block结构,后面的迭代中重复地使用这个结构,大大减小计算量。这个block结构也使得并行成为了可能,在进行节点的分裂时,需要计算每个特征的增益,最终选增益最大的那个特征去做分裂,那么各个特征的增益计算就可以开多线程进行。










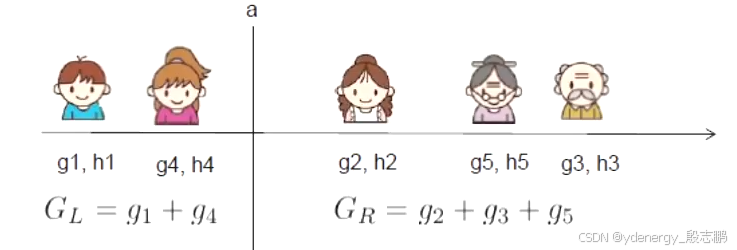


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










