数据科学、数据分析、人工智能必备知识汇总-----多元函数微分学-----持续更新

数据科学、数据分析、人工智能必备知识汇总-----主目录-----持续更新(进不去说明我没写完)：https://blog.youkuaiyun.com/grd_java/article/details/140174015

1. 偏导数

之前讲的导数，是针对一元函数来讲的。

偏导数是导数的推广，对于多元函数来说，如果只对其中一元求偏导，那么其它自变量就固定不动，看成常量。也就是说偏偏只对一个变量求导数

$\frac{dy}{dx}$是对x求全导数的，如果我们对多元函数求导，里面的x直接求导，而y,z,…都认为是关于x的函数，也要求导

---

$\frac{\partial f}{\partial x}$是对x求偏导数，对于多元函数求导，里面x直接求导，而其他的y,z,…都认为是常数。

$\frac{\partial f}{\partial x_0}=\frac{d}{dx}f(x,y_0){|}_{x=x_0}=f_x^{{}^{\prime }}(x_0,y_0)$

---

上面是对一元函数f(x,y_0)在x_0处导数的3种写法，都代表相同的意思

---

$\frac{\partial f(x_0,y_0)}{\partial x}=\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}$

---

$\frac{\partial f(x_0,y_0)}{\partial y}=\underset{\Delta y\to 0}{\lim }\frac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{\Delta y}$

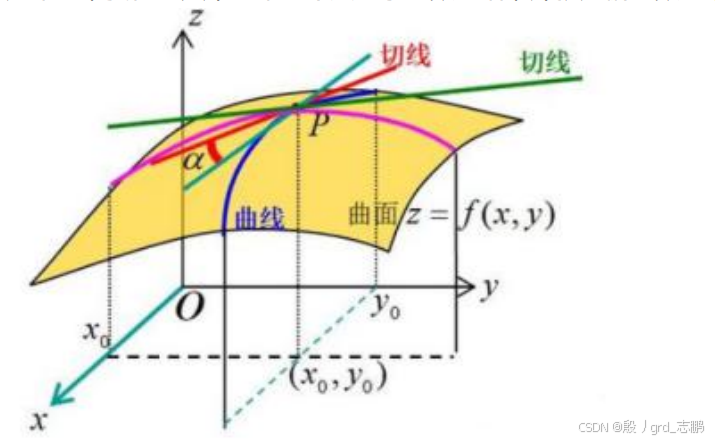
几何上面来讲的话,当我们将其它自变量全部设定为常数时，例如下图中，y恒定时，我们研究的曲线就是一个二维平面了，此时研究多元就变成了一元函数

---

---

就是在某个方向上对原函数来切一下，再去求导，就是偏导数

---

例子：已知$f(x,y)=x^2+xy-y^2$

---

$\frac{\partial f}{\partial x}=2x+y-0$

---

$\frac{\partial f}{\partial y}=0+x-2y$

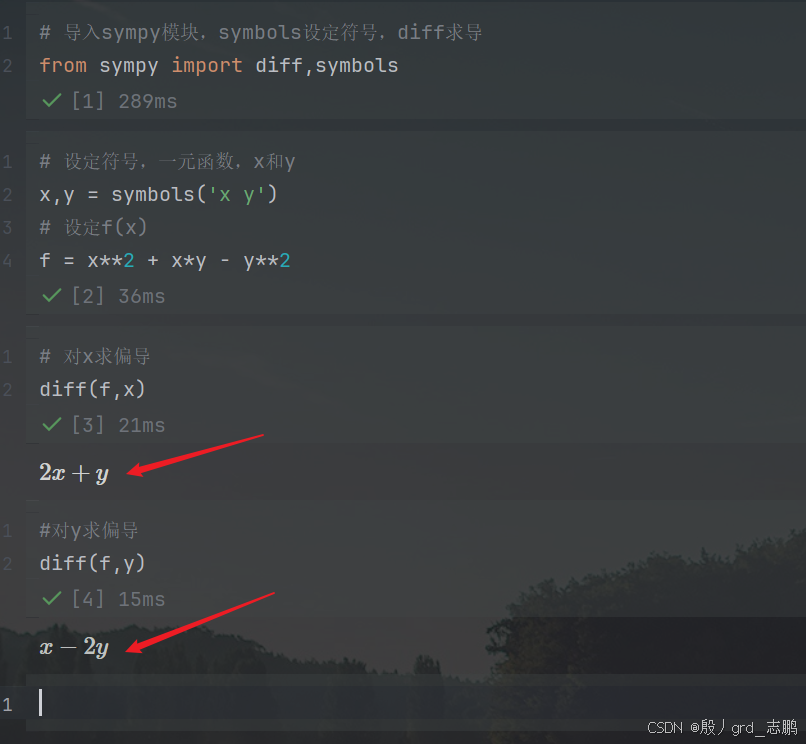
接下来用python来验证一下

# 导入sympy模块，symbols设定符号，diff求导
from sympy import diff,symbols
# 设定符号，一元函数，x和y
x,y = symbols('x y')
# 设定f(x)
f = x**2 + x*y - y**2
# 对x求偏导
diff(f,x)
#对y求偏导
diff(f,y)

2. 高阶偏导数

$\frac{{\partial }^{2}f}{省略}$：看上面，可以知道是对函数f求2阶偏导，而分母下面就是对谁求

---

$\frac{{\partial }^{2}f}{\partial x^2}=\frac{\partial }{\partial x}(\frac{\partial f}{\partial x})$：表示两次偏导都对x求

---

$\frac{{\partial }^{2}f}{\partial x\partial y}=\frac{\partial }{\partial y}(\frac{\partial f}{\partial x})$：表示先对x求偏导，再对y求偏导

---

$\frac{{\partial }^{2}f}{\partial y\partial x}=\frac{\partial }{\partial x}(\frac{\partial f}{\partial y})$：表示先对y求偏导，然后再对x求偏导

---

$\frac{{\partial }^{2}f}{\partial y^2}=\frac{\partial }{\partial y}(\frac{\partial f}{\partial y})$：表示两次偏导都对y求

---

所以和一元高阶导数差不多，只不过多元函数求高阶偏导，可以依次选择对哪个变量求

例子：设$f(x,y)=x^2+xy-y^2$

---

$\frac{{\partial }^{2}f}{{\partial }^{2}x}=\frac{\partial }{\partial x}(2x+y)=2$

---

$\frac{{\partial }^{2}f}{\partial x\partial y}=\frac{\partial }{\partial y}(2x+y)=1$

---

$\frac{{\partial }^{2}f}{\partial y\partial x}=\frac{\partial }{\partial x}(x-2y)=1$

---

$\frac{{\partial }^{2}f}{{\partial }^{2}y}=\frac{\partial }{\partial y}(x-2y)=-2$

此时我们可以发现$\frac{{\partial }^{2}f}{\partial x\partial y}$ = $\frac{{\partial }^{2}f}{\partial y\partial x}$，这就可以衍生出一个重要定理——偏导连续，混偏相同。也就是高阶导数和求导次序无关。

---

如果函数$z=f(x,y)$的两个二阶混合偏导数$f_{xy}^{{}^{\prime \prime }}(x,y)$及$f_{yx}^{{}^{\prime \prime }}(x,y)$在区域D内连续,则在区域D内恒有$f_{xy}^{{}^{\prime \prime }}(x,y)=f_{yx}^{{}^{\prime \prime }}(x,y)$,也就是$\frac{{\partial }^{2}f}{\partial x\partial y}$ = $\frac{{\partial }^{2}f}{\partial y\partial x}$

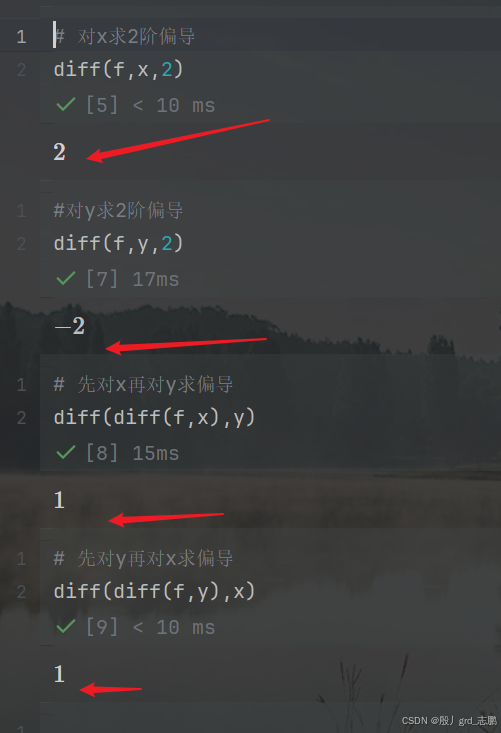
python验证一下

# 导入sympy模块，symbols设定符号，diff求导
from sympy import diff,symbols
# 设定符号，一元函数，x和y
x,y = symbols('x y')
# 设定f(x)
f = x**2 + x*y - y**2
# 对x求2阶偏导
diff(f,x,2)
#对y求2阶偏导
diff(f,y,2)
# 先对x再对y求偏导
diff(diff(f,x),y)
# 先对y再对x求偏导
diff(diff(f,y),x)

3. 梯度

机器学习中的梯度下降法和牛顿法很多地方都会用到梯度的概念

---

$\nabla f(x)$=$(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots ,\frac{\partial f}{\partial x_n}{)}^T$

---

梯度可以看成是一元函数它的导数，对于多元函数的推广。对于多元函数如果它的自变量有 N 个,例如$x_1{x}_2\cdots x_n$

---

那么它的梯度是个向量，是由对 $x_1{x}_2$ 等，不断的求偏导数构成的一个向量，称之为梯度

---

梯度我们用倒三角(nabla)这个符号来表示，作用于$f(x)$得到这样一个向量,式子里面的$T$表示往往我们把它转置一下，看成是列向量

4. 雅可比矩阵

本科高数不学的东西，就是由一阶偏导数构成的矩阵，发明它的目的主要是为了简化求导公式,对多元的复合函数求导,如果我们用雅可比矩阵来计算的话,它会写起来非常简洁,这在我们的人工神经网络反向推导的过程中往往会看到的

鉴于可能有人没学过神经网络，所以假设神经网络有两层A和B，A有3个神经元$x_1,x_2,x_3$，B有2个$y_1,y_2$。现在要A通过某函数f，3个节点映射到B的2个上，就需要用到这个矩阵

假设有这样一个函数$y_i=f(x_i)$可以把 $n维x向量$映射为$k维的向量y$

---

$\{\begin{array}{llc}y& =& f(x)\\ \uparrow & & \uparrow \\ k& & n\end{array}$

---

其中每个 $x_{\grave{ı}}$和每个 $y_i$ 都是相关的,也就是每个 $y_i$都是单独从 $x_i$映射过来的函数。它的雅可比矩阵就是每个 $y_i$ 分别对每个 $x_i$ 求偏导，然后构成的矩阵叫做雅可比矩阵

---

第一行就是 $y_1对x_1$、$x_2一直到x_n$ 求偏导，第二行就是 $y_2对x_1、x_2一直到x_n$求偏导，第k行就是 $y_k对x_1$、$x_2一直到x_n$求偏导

---

$\left[\begin{array}{cccc}\frac{\partial y_1}{\partial x_1}& \frac{\partial y_1}{\partial x_2}& \cdots & \frac{\partial y_1}{\partial x_n}\\ & & & \\ \frac{\partial y_2}{\partial x_1}& \frac{\partial y_2}{\partial x_2}& \cdots & \frac{\partial y_2}{\partial x_n}\\ & & & \\ \cdots & \cdots & \cdots & \cdots \\ & & & \\ \frac{\partial y_k}{\partial x_1}& \frac{\partial y_k}{\partial x_2}& \cdots & \frac{\partial y_k}{\partial x_n}\\ & & & \end{array}\right]$

---

如果 $x_i$ 是$n$维向量，y是k个值的结果,那么雅可比矩阵就是 $k\ast n$ 的矩阵

---

$\left[\begin{array}{c}{y}_1\\ \\ y_2\end{array}\right]\begin{array}{c}{y}_1=x_1^2+2x_1{x}_2+x_3\\ \\ y_2=x_1-x_2^2+x_3^2\end{array}\left[\begin{array}{c}{x}_1\\ \\ x_2\\ \\ x_3\end{array}\right]$

---

如果 $x_1,x_2,x_3$ 会映射成为 $y_1,y_2$，$y_1是x_1,x_2,x_3$ 的函数，$y_2也是x_1,x_2,x_3$ 的函数，那么它的雅可比矩阵是怎么构成的呢 ?

---

$\left[\begin{array}{ccc}2x_1+2x_2& 2x_1& 1\\ & & \\ 1& -2x_2& 2x_3\end{array}\right]$

5. Hessian 矩阵

对于一个多元函数来说的，它就相当于一元函数的二阶导数

---

怎么定义的呢?有一个n元函数，例如 $x_1，x_2直到x_n$

---

它的 hessian 矩阵是一个 n*n的矩阵，矩阵里面的元素是什么呢?

---

它的所有的元素是二阶偏导数构成的,第一个元素是对 $x_1$ 求二阶偏导数,第二个元素是对$x_1{x}_2$ 求偏导数，因为咱们前面讲过,多元函数高阶偏导数和顺序无关,所以 hessian 矩阵是对称矩阵

---

$\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1^2}& \frac{{\partial }^{2}f}{\partial x_1\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_1\partial x_n}\\ & & & \\ \frac{{\partial }^{2}f}{\partial x_2\partial x_1}& \frac{{\partial }^{2}f}{\partial x_2^2}& \cdots & \frac{{\partial }^{2}f}{\partial x_2\partial x_n}\\ & & & \\ \cdots & \cdots & \cdots & \cdots \\ & & & \\ \frac{{\partial }^{2}f}{\partial x_n\partial x_1}& \frac{{\partial }^{2}f}{\partial x_n\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_n^2}\end{array}\right]$

---

例子：$设f(x,y,z)=2x^2-xy+y^2-3z^2$，接下来按如下顺序依次求2阶偏导，然后一行一行放到矩阵中，就构成了 hessian 矩阵

---

$\frac{{\partial }^{2}f}{\partial x^2}=\frac{\partial }{\partial x}(4x-y)=4$

---

$\frac{{\partial }^{2}f}{\partial x\partial y}=\frac{\partial }{\partial y}(4x-y)=-1$

---

$\frac{{\partial }^{2}f}{\partial x\partial z}=\frac{\partial }{\partial z}(4x-y)=0$

---

$\frac{{\partial }^{2}f}{\partial y\partial x}=\frac{\partial }{\partial x}(-x+2y)=-1$**

---

$\frac{{\partial }^{2}f}{\partial y^2}=\frac{\partial }{\partial y}(-x+2y)=2$

---

$\frac{{\partial }^{2}f}{\partial y\partial z}=\frac{\partial }{\partial z}(-x+2y)=0$

---

$\frac{{\partial }^{2}f}{\partial z\partial x}=\frac{\partial }{\partial x}(-6z)=0$

---

$\frac{{\partial }^{2}f}{\partial z\partial y}=\frac{\partial }{\partial y}(-6z)=0$

---

$\frac{{\partial }^{2}f}{\partial z^2}=\frac{\partial }{\partial z}(-6z)=-6$

---

hessian矩阵为：$\left[\begin{array}{ccc}4& -1& 0\\ & & \\ -1& 2& 0\\ & & \\ 0& 0& -6\end{array}\right]$

Hessian 矩阵和函数的凹凸性是有密切关系的，如果 hessian 矩阵正定，可以说函数 f(x)是凸函数，如果是负定，它就是凹函数，矩阵正定怎么定义的呢 ?

6. 极值判别法则

之前的微积分基础中讲过，对于一元函数，f(x)的一阶导数等于0处有极值，当 f(x)的二阶导数大于 0时是极小值，当 f(x)的二阶导数小于0时是极大值，可以参考X的平方这个函数

---

https://blog.youkuaiyun.com/grd_java/article/details/144348388

---

多元函数的极值判别法则

---

首先 f(x)的一阶导数等于0,这点是驻点的话,那它就可能是极值点，它是极大值还是极小值或者不是极值怎么判定的 ?

---

看 hessian 矩阵，在 f(x)的一阶导数等于0处，就是驻点处

---

如果 hessian 矩阵是正定的话，函数在该点有极小值

---

如果 hessian 矩阵是负定的话，函数在该点有极大值

---

如果 hessian 矩阵不定，还需要看更高阶的导数

正定是线性代数的知识：https://blog.youkuaiyun.com/grd_java/article/details/144393637

---

对于任意向量$X\ne 0$,都有$x^{T}Ax>0$,那就是正定矩阵，如果是$\ge$的话，那就是半正定矩阵。怎么判断矩阵是正定的呢?

---

$X^{T}X$半正定:对于任意的非零向量$u$，$u{X}^{T}Xu=(Xu{)}^{T}Xu\stackrel{令v=Xu}{\to }{v}^{T}v\ge 0$

---

上面这个反正我是不想用，一般会根据以下几个原则去判断

---

矩阵的特征值全部大于0

---

矩阵的所有顺序主子式都大于 0，这个一般上学时候考试做题用的多，机器学习用的少，几乎没用过

---

矩阵合同于单位矩阵