面向边缘计算的应用放置编排器

面向应用放置的网络集成边缘计算编排器

摘要

为了将应用从具有高延迟响应的集中式云中分离出来，服务提供商开始关注边缘计算解决方案，以提供低延迟和改善用户体验。现有的边缘部署策略使用与网络相关的信息作为决策依据，但其设计和部署逻辑受限于网络无法被控制的假设。本文设计了一种在电信基础设施内运行并假设与接入和核心网络控制器协作的编排器（ECO）。因此，可以请求进行网络调整，从而使该编排器参与资源供给，并求解一个优化问题——与现有技术不同，该问题执行顺序组件放置，且不假设应用程序具有已知或固定的复制度。该编排器的功能依赖于启发式算法，其中包括基于预计算最短路径的启发式方法，该方法运行在多项式时间内（即远快于穷举搜索），并在约99%的测试场景中找到最优解。

关键词

边缘计算，应用放置

一、引言

自物联网出现以来，主要的系统设计都围绕云托管应用及其与集成感知与执行功能的终端设备之间的交互[8]。尽管云托管服务器提供了充足的处理能力和存储空间以支持多个用户，但随着客户端数量不断增加，产生的大量流量导致底层网络出现带宽瓶颈[10]。边缘计算通过将（服务器端）应用的多个实例推近至终端用户侧，同时保持编程模型不变，从而缓解了这一问题。因此，来自终端设备的流量路径更短，降低了延迟，并减缓了数据积聚。

尽管应用托管业务目前被云服务提供商（如亚马逊或微软）所垄断，但电信运营商一直在尝试进入这一领域。边缘计算为他们带来了巨大机遇，因为他们已经拥有边缘基础设施，即具备服务托管能力的蜂窝基站，目前这些基站仅作为与服务器端应用程序通信的中继点，而非用于托管应用。一种电信驱动的应用托管基础设施需要一个应用部署控制器，其架构应类似于ETSI MEC [5] 或 OpenStack [9] 的规范。相应地，其部署逻辑可以追求诸如最小延迟 [1] 或执行延迟 [12] 等目标。然而，所有这些研究都忽略了一个重要的观察点，而这一点可能改变当前应用托管格局：电信运营商掌控着网络以及整个基础设施，在应用放置操作之前、期间和之后以细粒度方式处理。考虑到这一点，我们开发了一款边缘计算编排器，与现有研究不同的是：i）该编排器与接入网和核心网的控制器进行交互；ii）持续进行应用放置直至满足其需求，并考虑请求网络和基础设施调整的选项；iii）将放置问题归约为最优子集选择 [4]，而非传统的装箱问题或背包问题 [2]。因此，该编排器采用专为动态网络设计的部署逻辑，有利于边缘应用部署。

II. 相关工作

相关工作有两个领域，即应用放置架构和应用放置算法。

关于应用放置架构，我们提到了OpenStack的 Nova调度器[9]和ETSI MEC的移动边缘编排器[5]。这两个组件都是将应用程序部署到最符合应用需求的计算节点上的架构的一部分。Nova[9]维护所有节点的视图，并基于聚焦于兼容性特性的过滤机制来确定虚拟机的放置。然而，它明确与OpenStack的网络组件断开连接，且不考虑来自应用提供商的需求。移动边缘编排器[5]，根据与计算、存储、延迟等相关的需求将应用程序部署到合适的主机上，但缺乏与网络层的接口，因此被迫忽略一些情况，例如：检测应用需求中的违规（如所需带宽或延迟阈值）或请求额外资源。最后，[3],[13]和[6]提供了有关相关架构和框架的进一步信息。

关于应用放置算法，相关研究工作可见于内容分发或云服务器管理等多个领域。在[1]中，作者提出了用于广域网上地理分布的云环境中的资源分配算法。假设计算任务所需的资源是先验已知的，并将问题建模为寻找具有可用资源的节点，以最小化由连接所选节点的链路引起的延迟值中的最大延迟。他们得出结论：基于子图选择的算法相较于其他方法具有显著优势。在[7]中，作者探讨了在内容分发网络背景下的放置问题，设计了在选定节点上复制和部署对象的启发式算法。

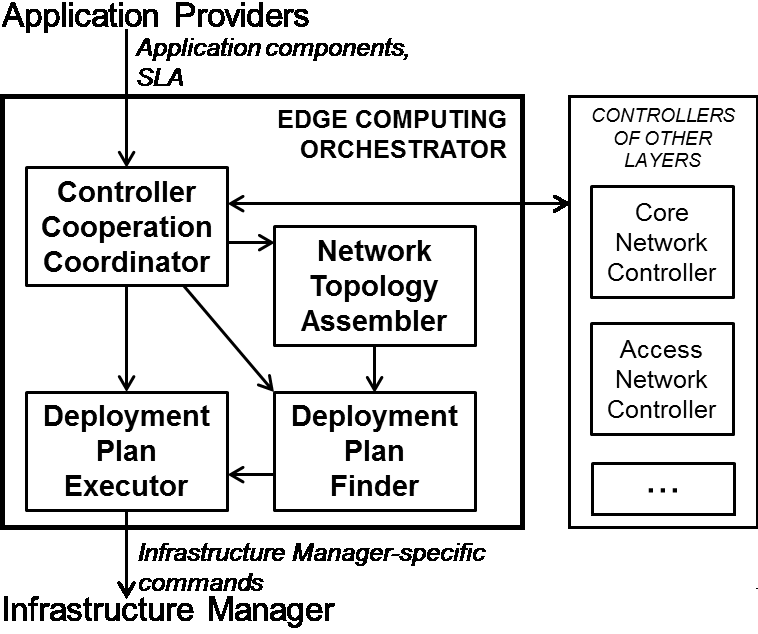
图1. ECO的高层架构

节点，以最小化与跳数相关的成本。结果表明，贪心算法可以获得接近最优的性能。在[12]中，部署用于解决将移动用户的工作负载分配到计算节点的问题。作者将云和边缘节点组织成树形层次结构，并开发了一种部署逻辑，将过载外包给层次结构中更高层的节点，优化目标是最小化执行延迟。最后，[11]针对故障场景进行处理，通过部署应用的冗余实例实现容错部署。

尽管文献中存在多种部署逻辑，但没有相关工作解决在支持任务复制但副本的最优数量未知的情况下，将具有相互需求的多个任务部署到多个节点上的确切问题。为了解决这个问题，我们在下一节中以不同的方式对任务放置进行了建模。

III. 边缘计算编排器

边缘计算编排器（ECO）是一种应用部署控制器，依赖于其他层的控制器来帮助满足应用需求。此类解决方案可带来商业利益，特别是对于电信运营商而言，因为他们是唯一能够原生实现这种多层协作的主体，能够以细粒度方式控制整个网络基础设施。

A. 架构

ECO的高层架构如图1所示，包括以下组件：

控制器协同协调器（CCC） ：它实现了一个接口，用于向其他网络控制器发送/接收请求。其用途包括：i) 提交应用程序及其服务等级协议（SLA），ii) 动态网络切片协商（指节点和链路的容量，这些信息对此应用程序保持私有），iii) 接收来自其他网络控制器的需求违规（在ECO不可见的层中）或重新配置请求（例如迁移和资源调整）。

网络拓扑组装器（NTA） ：它将控制器提供的资源所计算出的网络切片转换为与部署方案查找器（DPF）内部算法兼容的图表示。

部署方案查找器（DPF） ：它根据应用程序的服务等级协议（SLA）、网络切片以及客户端用户的位置（从接入网络控制器获取）来计算在计算节点上复制和部署应用程序的优化方案。

部署方案执行器（DPE） ：它接收来自DPE的放置计划或来自CCC的独立请求，并将其转换为可由基础设施管理器（例如，Nova调度器 [9]）执行的格式化命令。

请注意，由于引入了控制器间交互，才得以在接入网和核心网中基于指标实现动态切片协商和违规检测。

B. 问题表述

DPF根据本节中制定的优化问题来处理任务放置。该问题基于以下假设：i) 应用程序由组件组成，每个组件执行特定任务，并可独立于其他组件进行部署，但可能与其他组件交互。每个组件都配有一个唯一的优先级值，以反映其重要性。ii) 组件之间存在定量要求（例如延迟）。每个需求与一个组件相关联，并指向另一个更高优先级的组件（以避免重复需求）。iii) 应用程序旨在服务最终用户，因此最高优先级组件对客户端应用程序有需求。iv) 组件可以在各个计算节点上复制并部署。

网络切片是一组包含I个节点的集合C：$ C = {c_1, c_2, \dots, c_I } $。两个节点$ c_1 $和$ c_2 $之间的延迟表示为：$ Lat_{c_1,c_2} $。一个应用是包含J个可部署组件的集合E： $ E = {e_1, e_2, \dots, e_J } $，每个组件具有一组硬件要求Q：$ Q = {q_1, q_2, \dots, q_{X_e} } $，以及一组包含$ M_e $个延迟需求的集合R： $ R = {r_1, r_2, \dots, r_{M_e} } $。对客户端应用程序的需求将被重定向到集合C中距离客户端用户最近的节点。该信息通过接入网络控制器经由CCC共享。每个组件被视为独立的优化案例，并从最高优先级组件e开始，目标是找到一个集合 $ T \subseteq C $，使得在集合T的节点上复制和部署e时，能够使e的所有延迟需求的延迟总和最小。此外，要求实现最小延迟所需的e的复制数量最少（即集合T的基数）。因此，T的最小基数为：
$$ |T| \quad \text{with} \quad T \subseteq C \quad \text{and} \quad T = {c_1, c_2, \dots, c_k } $$

受限于各组件 e 的延迟要求的延迟之和的最小值：
$$ \sum_{r_1}^{r_M} Lat_{c_a,c_b} $$

其中$ c_a \in C $为需求r所指向组件的宿主节点，$ c_b \in T $为在硬件约束下（即组件的硬件要求受限于相应节点的容量，例如CPU、内存、存储）相对于$ c_a $具有最小延迟的节点。

为了证明复杂度，我们将该问题重新表述为最优子集选择[4]的一个实例。搜索空间是一个集合A，它包含C的所有可能子集，共由$ 2^{|C|} $项组成。最优解是A中满足优化目标需求（即最小延迟和复制）且符合硬件约束的项。最优子集选择在一般形式下已知是NP难的，因此该问题具有相同的复杂度。在大规模数据集上求解NP难问题的最优解变得不切实际，因此在下一节中，我们开发了适用的启发式算法。

C. 部署启发式算法

在本节中，我们开发了基于优化目标计算最优和近似最优解的启发式算法。伪代码遵循问题表述中的符号，并且仅对一个组件进行放置。对于应用的其余组件，采用相同的逻辑按优先级依次循环执行。

1) 基于穷举的最优部署（OPE）

该启发式方法搜索整个搜索空间以找到最优解。其时间复杂度为指数级。

算法1：OPE
输入：C, e | 输出：dp
int minSumLatency= INF;//用于保存找到的min值的变量f or循环 成本函数。初始值设为INF。
int sumLatency;//用于存储成本函数的临时值的变量， 即，f or循环每个被检查的可能解。
列表 currSubset；// 一个列表变量，用于存储每个可能的节点部署计划，即C的每个子集。
List selectedNodesList;// 一个列表变量，用于存储当前子集的节点具有足够资源来托管该组件的。
for循环 ( i = 0; i< 2^|C|; i++){// 2^|C| 可能的部署计划…
当前子集 = C.getSubset(i);// 返回C的第i个子集（即 此外，一个计算节点的列表
selectedNodesList ={};
for循环 ( j = 0; j < |当前子集|; j++){
如果 ( 当前子集[j] .适合(e) ){ // 如果当前子集中的第 j 个节点适合 ( e ) ，则返回 trueth 节点在当前子集中可以托管组件e，否则为假
selectedNodesList.add(currSubset[j]);
} }
sumLatency= e.sumLatencyIfDeployedOn(selectedNodesList);// 返回当 e 被部署在每个位置时成本函数的值 nodesList 的节点之一
if (sumLatency < minSumLatency){
dp = selectedNodesList; minSumLatency = sumLatency } }
return dp;// 组件将要部署的节点列表

2) 贪婪放置无限制（GPU）

该启发式方法将每个组件部署在所有具有足够资源来托管它的节点上。其时间复杂度为线性。

算法2：GPU
输入：C, e | 输出：dp
List selectedNodesList;// 用于存储所选节点的列表变量
有足够的资源来托管该组件.
for循环 ( i = 0; i < |C|; i++){
如果 ( C[i].适合(e) ){
selectedNodesList.add(C[i]);
} } dp = selectedNodesList;
return dp;// 部署该组件的节点列表

3) 带成本阈值的贪心放置（GPC）

In this heuristic, the node that results in mini 最大延迟被选为复制和放置的依据，直到优化目标的与延迟相关的指标的值低于阈值。时间复杂度是多项式。

算法3：GPC
输入： C, e, 阈值 | 输出： dp
int minSumLatency= INF;//用于保存成本函数找到的最小值的变量。初始值设为无穷大。cost function. Initially set to infinity. int sumLatency;//用于保存成本函数的临时值的变量，即针对每个被检查的可能解。 List selectedNodesList;//一个列表变量，用于存储每次迭代中导致最小成本的节点minimum cost in each iteration.int bestNodeIndex;//一个变量，用于记录每次迭代中使成本函数取得最优值的节点索引.the best value of the cost function in each iteration. for循环 ( i =0; i<|C|; i++){ minSumLatency = INF; for循环 ( i =0; i<|C|; i++){ if ( C[i].适合(e) & C[i]不在…中 selectedNodesList){ selectedNodesList.添加(C[i]); sumLatency = e.sumLatencyIfDeployedOn(selectedNodesList); // 返回当组件 e 部署在节点列表中的每个节点上时成本函数的值 if (sumLatency < minSumLatency) { bestNodeIndex = i; minSumLatency = sumLatency; } selectedNodesList.移除(C[i]); } } selectedNodesList.添加(C[bestNodeIndex]); if (minSumLatency ≤阈值) { 跳出; } } dp = selectedNodesList; return dp; // 组件应被部署的节点列表

4) 基于最短路径的优化放置 (PSP)

对于每个组件所引用的宿主节点，该启发式方法选择最短路径中的节点拥有足够资源来部署待部署组件的控制器。请注意，这种方法得益于控制器之间的通信，因为ECO可以访问核心网络信息。核心网络控制器维护拓扑的静态视图，并且仅在初始化时计算一次最短路径，但在请求时会将这些值共享给ECO。无需计算最短路径降低了启发式方法的时间复杂度，该时间复杂度为多项式。

算法4 PSP
输入: C, e | 输出: dp
List selectedNodesList;// 用于存储已选节点的列表变量 已被选入最优部署方案。
列表 examinedNodes；//一个初始为空的列表，用于存储已检查的节点
已经过检查以托管该组件的副本。
列表 R = e.getRequirements();//返回一个需求列表 R（包含 组件e到其他已部署组件的副本），其中 R[i]是第 i 个需求，而 R[i].host 是放置该需求的节点 此需求所指的复制被托管。
for循环 ( i = 0; i < |R|; i++& R[i].host 不在…中 已检查节点){
已检查节点.add(R[i].host); //下面的“排序命令”实际上对应一个单一操作 检索相应（已排序）的列表 排序_的_元素_的_C_基于_到_最短路径_路径_至_R[i].host；
for循环 ( j=0; j<|C| ; j++){
if( C[j].适合(e) & C[j]不在…中 selectedNodesList){ //返回 true
如果C中第j个节点可以托管组件e且不在
selectedNodesList
selectedNodesList.add(C[j]);
跳出
}}}
dp = selectedNodesList;
return dp;//组件将要部署的节点列表

IV. 评估

使用基于Java的实现的ECO，并通过模拟其余基础设施，我们进行了一项评估，重点在于所开发启发式算法的最优性（或近似最优性）。我们使用了四种拓扑结构（分别包含6、8、10以及12个节点），并为每个场景模拟10000个部署场景。每个场景通过为与基础设施相关的变量分配随机值来创建，例如：链路延迟（1‐20）、节点CPU核心（0‐10）、节点内存（0‐2000）、节点存储（0‐4000）；以及与应用组件相关的变量，例如：依赖组件数量（1‐4）、CPU核心（1‐5）、内存（100‐1000）、存储（200‐2000）。

图4. 每种启发式方法找到最优部署方案的次数 （即与OPE相同）。

图2. GPC 为达到由成本阈值指示的延迟所需 的每个需求的平均复制次数。

图3. 每个需求在每种启发式方法中为找到 最小延迟所需的平均复制次数。

图3显示了每种启发式方法为实现最小延迟所需的每个需求的平均复制次数。请注意，由于置信区间（99%）重叠，OPE和PSP非常接近。

图4显示了每种启发式方法成功计算出最优解的次数。注意，尽管节点数量增加，PSP 与 OPE 极为接近，而 GPC 和 GPU 的成功率则下降。

图2基于GPC的性能，展示了随着阈值逐渐增加，复制数量减少，从而降低了网络切片内已使用资源的数量。成本阈值表示优化目标中组件需求延迟的和，因此单位相同。因此，GPC还描绘了复制数量与有效延迟之间的权衡，并提供了根据应用提供商需求调整此权衡的机制。

V. 结论

我们提出了一种边缘计算编排器的架构及其内部算法，该编排器在电信驱动的应用托管基础设施中执行应用组件的复制和放置。该编排器实现了与接入和核心网络控制器协作的接口。这导致了一种不同于现有技术（例如，动态网络切片协商、顺序组件放置）的部署逻辑，从而涉及不同的放置优化问题及相应的启发式算法。在所开发的启发式算法中，我们重点提出了基于最短路径的放置（PSP），它是唯一能够在多项式时间内接近最优解的方案。