[LeetCode]Range Sum Query

https://leetcode.com/problems/range-sum-query-mutable/

求i ~ j位置和

由于题干中说sum和update操作频率相同，区间求和考虑两种做法：树状数组和线段树。

树状数组：

理解关键在明白树状数组的结构图，

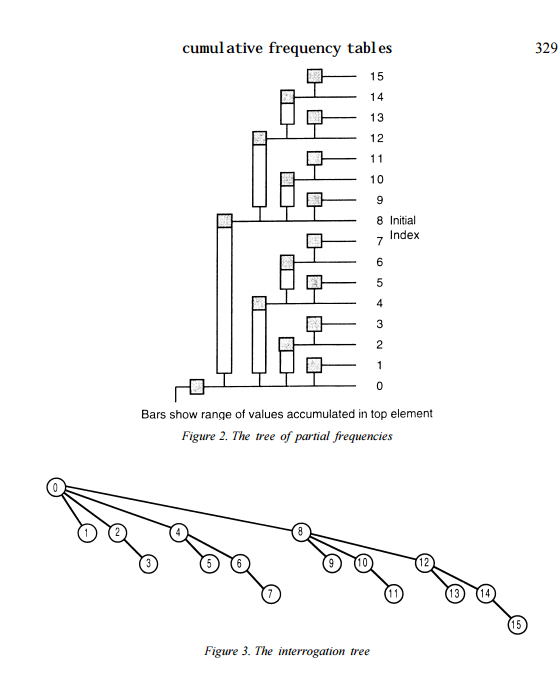
理解如何求sum和update的过程主要是

// 就是把k的二进制的高位1全部清空，只留下最低位的1

(i & -i)

init和update函数传入的都是index和这个index要更新的值，BIT多开一位，所以相关i都要先自增一位。初始化update的时候一直加，上界是n；查询getSum是一直减，下界是0。

public class NumArray {
    
    int[] BIT;
    int[] nums;
    int n;


    public NumArray(int[] nums) {
        this.nums = nums;
        n = nums.length;
        BIT = new int[n + 1];
        for (int i = 0; i < nums.length; i++) {
            init(i, nums[i]);
        }
    }
    
    private void init(int i, int val) {
        // 由于BIT长度为n+1，所以每次都要先i++一下
        i++;
        while (i <= n) {
            BIT[i] += val;
            i += (i & -i);
        }
    }


    void update(int i, int val) {
        int diff = val - nums[i];
        nums[i] = val;
        init(i, diff);
    }


    public int sumRange(int i, int j) {
        return getSum(j) - getSum(i - 1);
    }
    
    private int getSum(int i) {
        i++;
        int sum = 0;
        while (i > 0) {
            sum += BIT[i];
            i -= (i & -i);
        }
        return sum;
    }
}

线段树：

节点内有beg、end两个参数表示该节点所表示的sum的范围是从beg到end。显然当beg==end时，sum=nums[beg]。也就是说，线段树中叶子节点表示nums[i]的值，非叶子结点表示一个区间和。sum和update显然也是要用到递归操作（毕竟是树）。

节点的左子树是beg~mid范围的和，右子书是mid+1到end范围的和。

public class NumArray {

    class SegmentTreeNode {
        int start, end;
        SegmentTreeNode left, right;
        int sum;

        public SegmentTreeNode(int start, int end) {
            this.start = start;
            this.end = end;
            this.left = null;
            this.right = null;
            this.sum = 0;
        }
    }
      
    SegmentTreeNode root = null;
   
    public NumArray(int[] nums) {
        root = buildTree(nums, 0, nums.length-1);
    }

    private SegmentTreeNode buildTree(int[] nums, int start, int end) {
        if (start > end) {
            return null;
        } else {
            SegmentTreeNode ret = new SegmentTreeNode(start, end);
            if (start == end) {
                ret.sum = nums[start];
            } else {
                int mid = start  + (end - start) / 2;             
                ret.left = buildTree(nums, start, mid);
                ret.right = buildTree(nums, mid + 1, end);
                ret.sum = ret.left.sum + ret.right.sum;
            }         
            return ret;
        }
    }
   
    void update(int i, int val) {
        update(root, i, val);
    }
   
    void update(SegmentTreeNode root, int pos, int val) {
        if (root.start == root.end) {
           root.sum = val;
        } else {
            int mid = root.start + (root.end - root.start) / 2;
            if (pos <= mid) {
                 update(root.left, pos, val);
            } else {
                 update(root.right, pos, val);
            }
            root.sum = root.left.sum + root.right.sum;
        }
    }

    public int sumRange(int i, int j) {
        return sumRange(root, i, j);
    }
    
    public int sumRange(SegmentTreeNode root, int start, int end) {
        if (root.end == end && root.start == start) {
            return root.sum;
        } else {
            int mid = root.start + (root.end - root.start) / 2;
            if (end <= mid) {
                return sumRange(root.left, start, end);
            } else if (start >= mid+1) {
                return sumRange(root.right, start, end);
            }  else {    
                return sumRange(root.right, mid+1, end) + sumRange(root.left, start, mid);
            }
        }
    }
}