数据结构 树和二叉树概念解析

 ppt还是有用的

满二叉树

1. 术语详解

根：根结点(没有前驱)。

叶子：终端结点(没有后继)。

树：树是n（n>0）个结点的有限集。一棵树应满足以下条件：有且仅有一个特定的称为根的结点。（无前驱）当n>1时，其余结点可分为m（m>0)个互不相交的有限集T1，T2……Tm，其中每个集合本身又是一棵树。（子树）

有序树：结点各子树从左至右有序，不能互换（左为第一）。

无序树：结点各子树可互换位置。

森林：指m棵不相交的树的集合(例如删除A后的子树个数)。

双亲：即上层的那个结点(直接前驱)。

孩子：即下层结点的子树的根(直接后继)

兄弟：同一双亲下的同层结点（孩子之间互称兄弟）。

堂兄弟：即双亲位于同一层的结点（但并非同一双亲）。

祖先：即从根到该结点所经分支的所有结点。

子孙：即该结点下层子树中的任一结点。

结点：即树的数据元素。

结点的度：结点挂接的子树数。

结点的层次：从根到该结点的层数（根结点算第一层）。

终端结点：即度为0的结点，即叶子。

分支结点：即度不为0的结点（也称为内部结点）。

树的度：所有结点度中的最大值。

树的深度(或高度)：指所有结点中最大的层数。

二叉树：每个结点至多有两棵子树（即二叉树中不存在度大于2的结点），且二叉树有左右之分（有序），其次序不能任意颠倒。

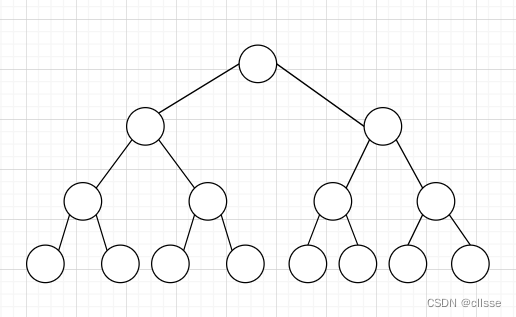
完全二叉树：只允许最后一行不为满，且最后一行必须从左往右排序，最后一行元素之间不可以有间隔。

1.   二叉树中每一层结点的个数达到最大，即没有度数为1的结点。
2.   叶子全部都在最深的那一层。
3.   任一结点，若其右分支下的子孙的最大层数为i，则左分支下的子孙最大层数必为i或i+1（左子树编号一定在右子树之前）。
4. 具有n个结点的完全二叉树的深度为floor(log_{2} n)+1。

完全二叉树

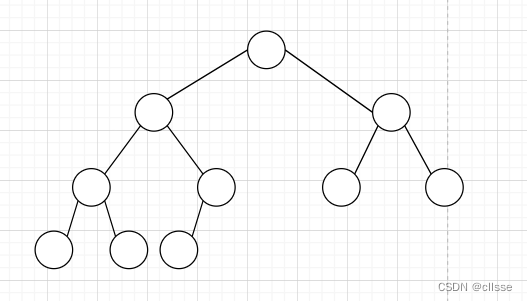
满二叉树：二叉树中每一层结点的个数达到最大。即没有度数为1的结点。一个层数为k的满二叉树总结点数为:2^k-1。

二叉排序树(二叉搜索树，二叉查找树)：

（1）若左子树不空，则左子树上所有结点的值均小于或等于它的根结点的值；
（2）若右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
（3）左、右子树也分别为二叉排序树；

线索：指向结点前驱和后继的指针叫做线索。

线索二叉树：每个结点上加上线索的二叉树。Tag为0表示lchild/rchild指示孩子，Tag为1表示指示前驱或后继。

线索化：对二叉树以某种顺序遍历使其变为线索二叉树的过程。

路径长度：从树中一个结点到另一个结点之间的分支构成的路径，分支数目称为路径长度。

树的路径长度：从树根到每一个结点的路径长度和。对于结点个数相同的树。

完全二叉树是路径长度最短的树。

哈夫曼树是带权路径长度最短的树。

树的带权路径长度：树中所有叶子结点的带权路径长度和。

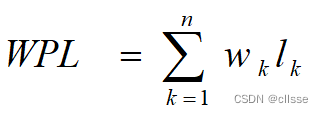
哈夫曼树(最优二叉树)：具有n个叶子结点(每个结点的权值为wi) 的二叉树不止一棵，但在所有的这些二叉树中，必定存在一棵WPL值最小的树，称这棵树为Huffman树(或称最优树) 。分为左小右大和左先右后两种构造方法。

2. 树的存储结构

顺序存储：用一组地址连续的存储单元依次自上而下、自左而右地存储二叉树。容易形成空间的浪费，只适合完全二叉树。

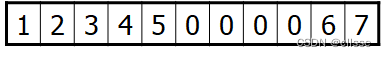
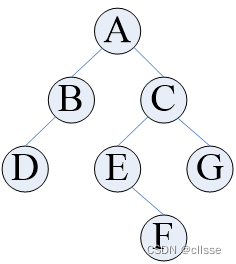
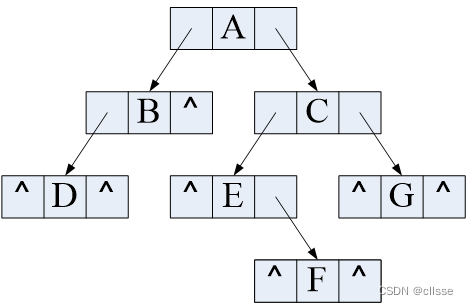
链式存储：

• 二叉链表：三个域（数据域、左、右指针）
• 三叉链表：四个域（数据域、左、右指针、双亲指针）

 

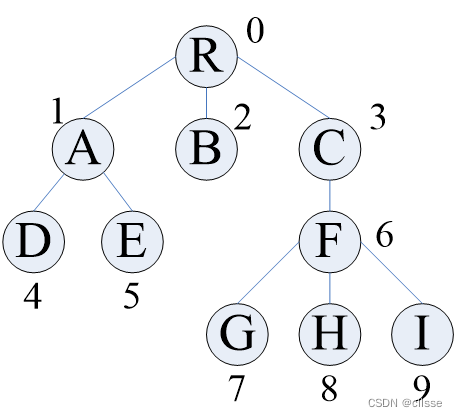
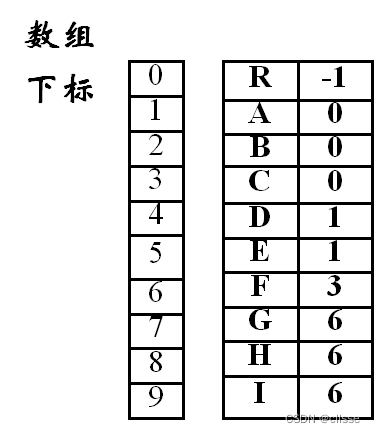
双亲表示法：假设一组连续空间存储树的结点，同时在每个结点中附设一个指示器指示其双亲在链表中的位置。

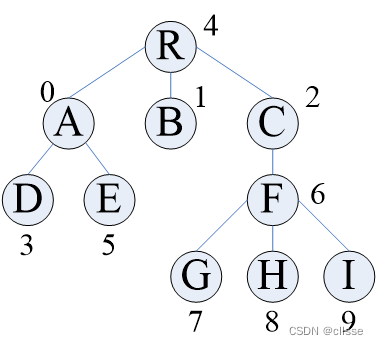
孩子表示法：多重链表，每个指针指向一棵子树的根结点。

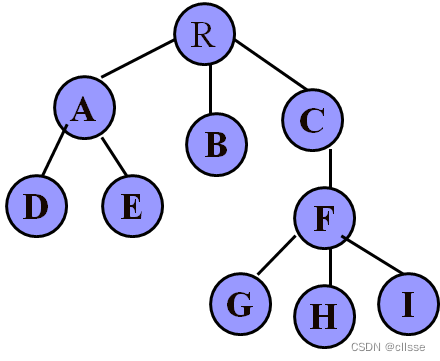
孩子兄弟表示法：二叉树表示法，链表中两个链域分别指向该结点的第一个孩子和下一个兄弟结点。

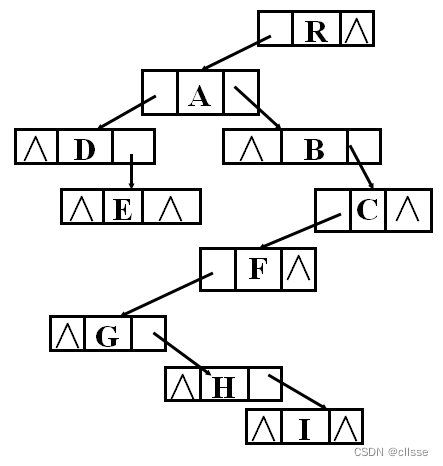
3. 二叉树的遍历

不是完全二叉树

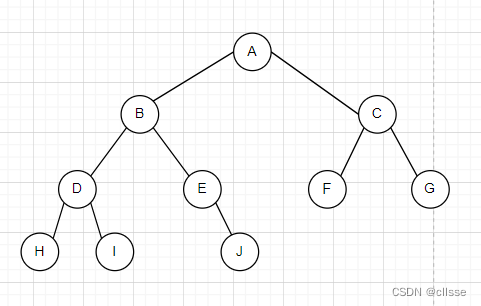
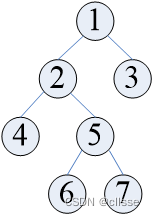
先序遍历：根左右 ABDHIEJCFG

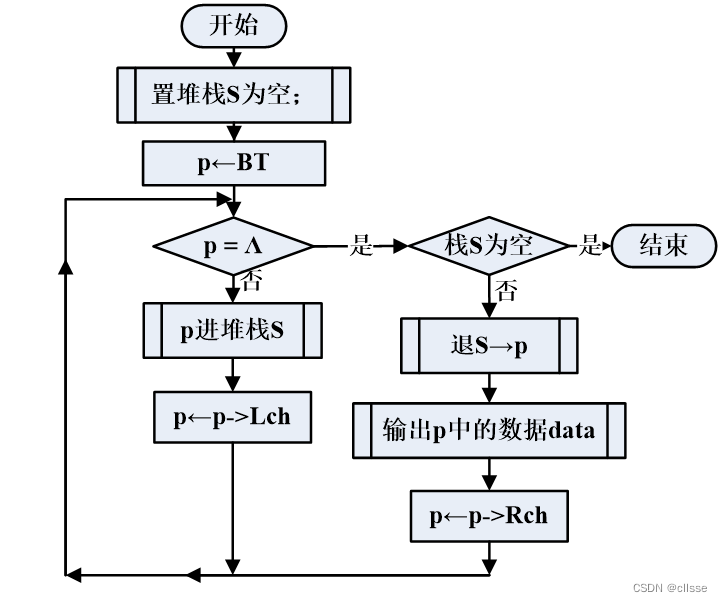
中序遍历：左根右 HDIBEJAFCG

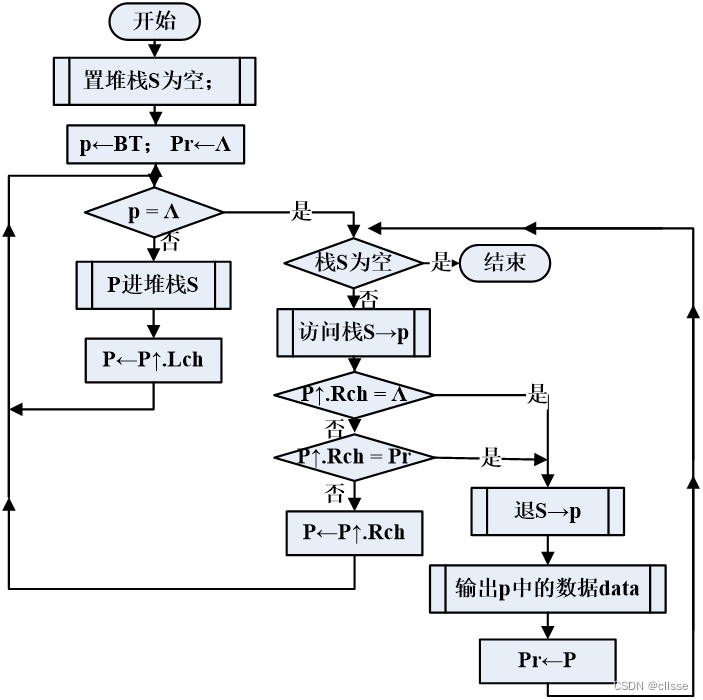
后序遍历：左右根 HIDJEBFGCA

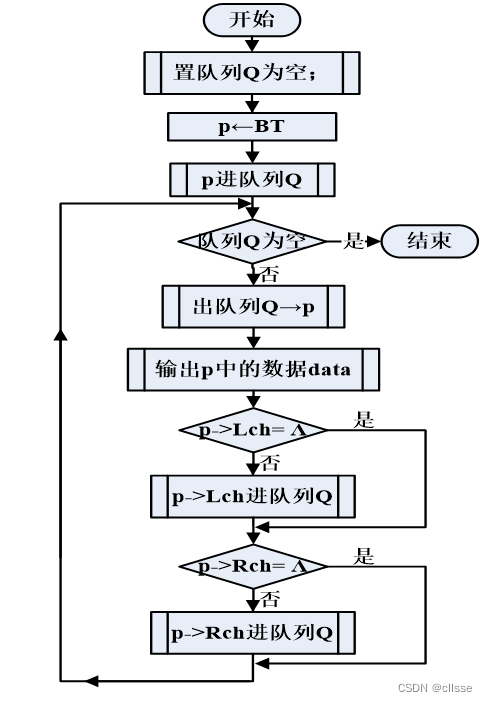
层次遍历：按层次遍历。ABCDEFGHIJ

先序遍历非递归算法

中序遍历的非递归算法

后序遍历非递归算法

层次遍历

4. 树，二叉树与森林的转换

1.树->二叉树

树，E,I都要当成左子树

连接兄弟

对每个结点，除了其左孩子外，抹掉其与其余孩子之间的连线。

当前结点左子树不变，右子树是当前结点的兄弟

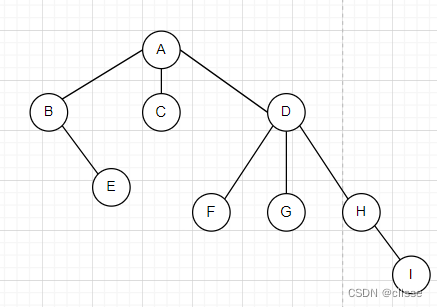
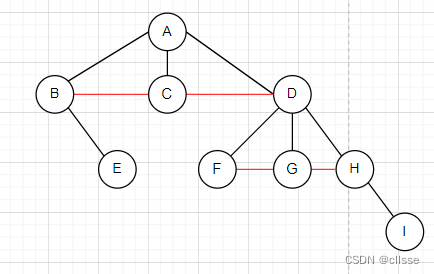
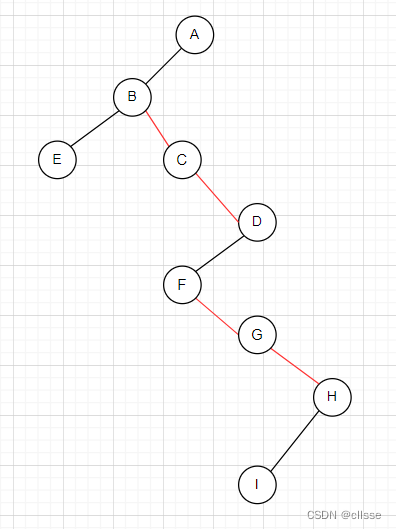
2.二叉树->树

上面过程倒过来做就行。

3.森林->二叉树

若森林F为空，则二叉树B为空树；

若F不为空，将森林的每棵树转化为二叉树(孩子兄弟表示法)，第一棵二叉树的根为整棵二叉树的根。

将各二叉树的根结点视为兄弟结点，再完成二叉树的转化

森林

每棵树转化成二叉树

合并成二叉树

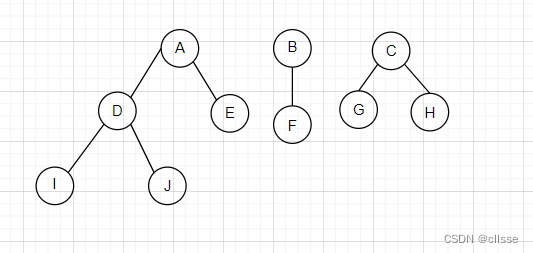
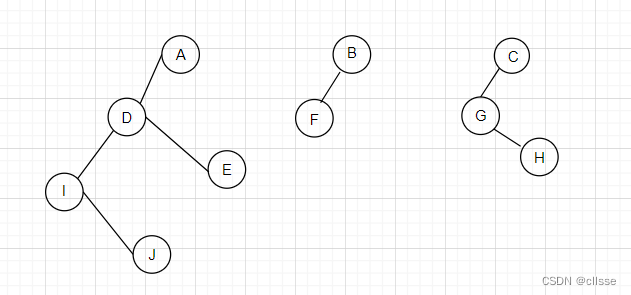
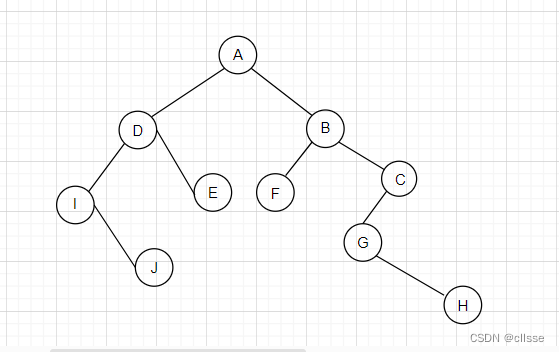
4.二叉树->森林

若B为空，则F为空；

若x为y的左孩子，则将x的右子孙与y相连

去掉所有双亲到右孩子的连线。

5. 树的相关计算

1. 计算哈夫曼树WPL

如上图，WPL=3*(10+12)+3*13+4*(4+9)+2*(28+29)=66+39+52+114=271

2. 三叉树各个度结点的关系

设三叉树度为0，1，2，3的结点分别为a,b,c,d个,

结点总数 n=a+b+c+d

孩子总数 m=b+2c+3d

 n=m+1

=>   b+2c+3d=a+b+c+d

=>  a=c+2d

3.根据先序遍历和中序遍历求后序遍历。根据后序遍历和中序遍历求先序遍历。

4. 二叉树的性质

1. 一棵深度为h（h≥1）的完全二叉树最多有2^h -1个结点(满二叉树)，最少2^(h-1)个结点。
2. 一颗有n个结点的满二叉树共有(n-1)/2个。
3. 二叉树叶子节点在前中后序遍历中的相对次序不变。

 1可以根据等比数列求和公式可知。