一些关于深度聚类以及部分对比学习的论文阅读笔记

资料

深度聚类算法研究综述(很赞，从聚类方法和深度学习方法两个方面进行了总结，我这个可能作为综述前的一篇文章，要是捋出头绪也写一写):https://www.cnblogs.com/kailugaji/p/15574267.html
对比学习代码库：https://github.com/HobbitLong/PyContrast?tab=readme-ov-file

SwAV

论文：https://arxiv.org/pdf/2006.09882
代码：https://github.com/facebookresearch/swav
视频(像我一样的小白必看)：https://www.bilibili.com/video/BV1754y187Ki/?spm_id_from=333.337.search-card.all.click

问题

现有的方法通常是在线工作的，依赖于大量的显示的成对特征的比较，在计算上是有挑战性的。

方法

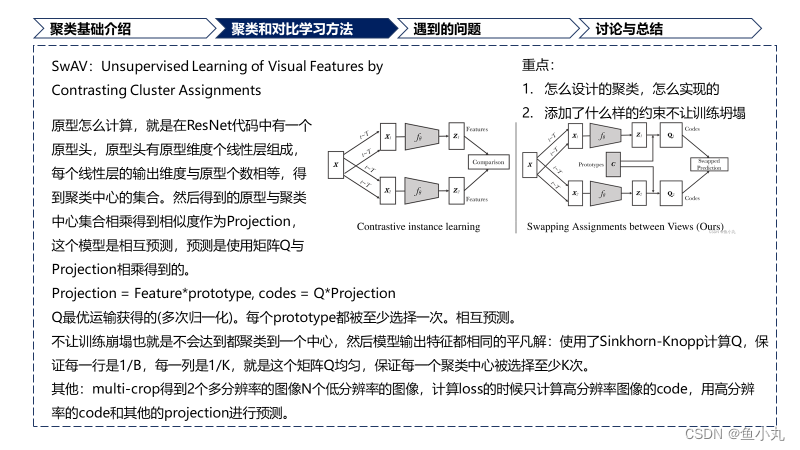
提出了SwAV，不需要成对进行比较。方法同时对数据进行聚类，同时价钱同一图像不同增强之间的一致性，不是像对比学习一样直接表示特征。
提出了新的数据增强multi-crop，在不增加内存或计算需求的情况下，使用不同分辨率的视图混合代替两个全分辨率视图。

方法的创新点

不需要进行成对比较。
我们的方法是内存有效的，就是不需要大的memory bank或者特殊的动量网络。

为什么有效

$L(zt,zs)=l(z_t,q_s)+l(z_s,q_t),$
通过将一组特征匹配到一组K个原型中来计算他们的code $q_t,q_s$。
假设：两个特征包含相同的信息，那么是可以通过其中一个feature去预测另一个的code的。

有什么可以借鉴的地方

聚类

聚类前的特征先投影到单位球面上得到$z_{nt}$。
然后把$z_{nt}$映射到K个可训练的原型向量上，得到$code$。
如何计算code
SwAV的损失建立了从feature $z_s$到预测code $q_t$，从$z_t$到预测code $q_s$的交换预测的问题。损失是CE Loss，是计算的code和$z_i$和所有在$C$中的原型之间的点积计算softmax得到的概率值。
$l(z_t,q_s)=-\sum _k{q}_s^{(k)}\log p_t^{(k)}$
where $p_t^{(k)}$是第t个feature $z_t$与第k个clusterinng centroid $c_k$进行乘积然后乘以$\frac{1}{\tau }$计算softmax。

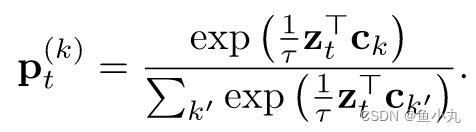
下面这个式子是把展开后的$p_t^{(k)}$带入到损失中，然后拆开得到的，前面两个是分子，后面是分母。

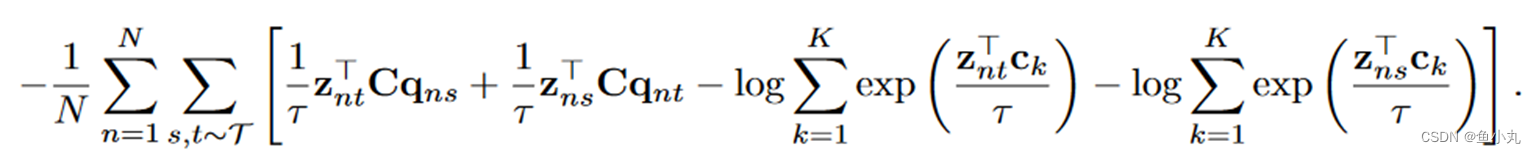
原型C的跨批次使用，SwAV将多个实例聚类到原型。使得同一个批次中所有的样本都被原型等分。约束了不同图像的编码是不同的，避免了每个图像都有相同编码的平凡解。
使用Q矩阵把特征映射到原型，优化Q来最大化特征和原型之间的相似性。
$\underset{Q\in Q}{\max }Tr(Q^T{C}^{T}Z)+\epsilon H(Q),$
H(·)是熵，控制映射是平滑的，但是强的熵正则化会导致平凡解，模型会坍塌，所以保持$\epsilon$要小。
对Q矩阵进行约束。
Q = { Q ∈ R + K × B + ∣ Q 1 B = 1 K 1 K , Q T 1 K = 1 B 1 B } , Q= \{ Q ∈ R^{K×B}_{+} + | Q_{1B} = \frac{1}{K} 1_K , Q^T1_K = \frac{1}{B} 1_B \} , Q={ Q∈R+K×B​+∣Q1B​=K1​1K​,QT1K​=B1​1B​},
式中：1K表示K维向量。这些约束要求批次中平均每个原型至少被选择B K次。使用连续的Q*，不进行离散化，因为获得离散码所需的舍入是比梯度更新更激进的优化步骤。在使模型快速收敛的同时，却导致了更差的解。
在集合Q上，取正规化指数矩阵的形式。
$Q^{\ast }=Diag(u)exp($