vector关于”异或“知识点的OJ题

在正式开始讲解题目之前，我们有必要复习一下关于异或^,按位与&的知识点。

函数返回参数二进制中 1 的个数的不同方法-优快云博客

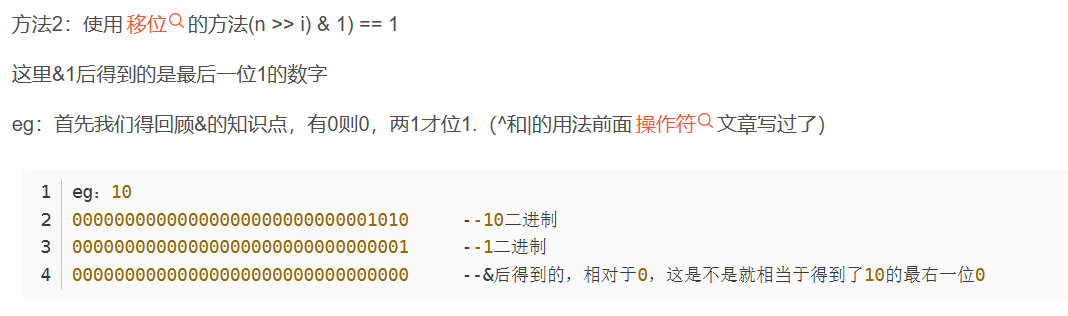
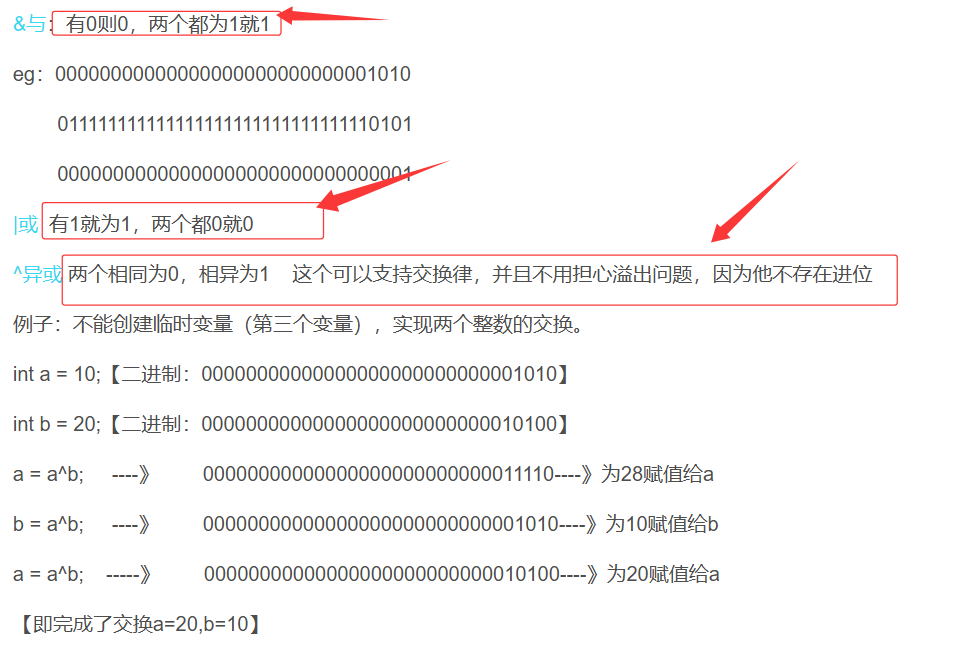
*************补充：*********************

OJ（一）只出现一次的数字1

136. 只出现一次的数字 - 力扣（LeetCode）

我们上面知道：

异或^：相同为0，相异为1.，且支持交换律

讲解：

1. 由上面的题目知道，只有一个数字只出现了一次，其余的都出现了两次。

2.那么，我们就可以利用异或这个性质，把它们全部的数字都异或一遍，那么，出现两次的数必定会变成0，而只出现一次的数，仍然是它本身。（它的恒等律）

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int len=nums.size();
        int val=0;
       //写法一：
       // for(int i=0;i<len;i++)
      //  {
      //      val ^=nums[i];
      //  }
    
       //写法二： 
      for(auto e:nums)
      {
        val ^=e;
      }
        return val;
    }
};

 OJ（二）只出现一次的数字2

137. 只出现一次的数字 II - 力扣（LeetCode）

方法一：2. 对数据进行排序，然后找出只出现1次的数字，缺点：时间复杂度不是O(N) 而题目要求了，时间复杂度必须为O(N)线性时间复杂度

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        if(nums.size()==1){
            return nums[0];
        }
        sort(nums.begin(),nums.end());
        for(int i = 0; i< nums.size()-1;i+=3){
            if(nums[i]!=nums[i+2]){
                return nums[i];
            }
        }
        return nums[nums.size()-1];
    }
};

方法二：

题目说：只有一个数字出现一次，其余数字均出现3次，假设数组为{3,5,3,3}
通过分析可知：
3的二进制：0 0 0 0 0 0 1 1
5的二进制：0 0 0 0 0 1 0 1
3的二进制：0 0 0 0 0 0 1 1
3的二进制：0 0 0 0 0 0 1 1
          0 0 0 0 0 1 3 4  二进制1的总数
对于出现3次的数字，各位出现的次数都是3的倍数，因此对统计的为1的比特总数%3
          0 0 0 0 0 1 0 1 = 5
          结果就是只出现一次的数字

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ans=0;
        for(int i=0;i<32;i++)
        {
            // 统计该每个数字第i个比特位为1的总数
            int total=0;
            for(auto num:nums)
            {
                total +=((num>>i)&1);
            }
            // 如果total能够被3整除，说明只出现一次的数字在该位置上一定是0
            // 否则在该位置上一定是1
            if(total%3 !=0)
            {
                ans |=(1<<i);
            }
        }
        return ans;
    }
};

 ans |=(1<<i);  这行代码的效果是，将 ans  的二进制表示中第 i  位与 1<<i  的二进制表示（只有第 i  位为 1 ，其他位为 0 ）进行按位或操作，从而将 ans  的第 i  位设置为 1 。这是为了根据统计每个数字第 i  个比特位为 1  的总数来确定最终结果中对应位的值。

OJ（三）只出现一次的数字3

260. 只出现一次的数字 III - 力扣（LeetCode）

方法一：排序法（ps：这道题也可以使用我在优选算法那专题的双指针法，也是相似的做法）

*思路：

* 1. 从前往后遍历，若出现两次，则为相同元素，索引加2

* 2. 若出现一次（前后不等），则为所需要的数，存入vector，索引加1

* 3. 若没到尾后位置，说明最后一个元素为出现一次的数

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        vector<int> ret = {0,0};
       
        int left = 0, i = 0;
        

        while (left < n-1)
        {
            if (nums[left] == nums[left+1])
            {
                left += 2;
                
            }
            else
            {
                ret[i++] = nums[left];
                left++;
            }
        }
        if (nums[n - 1] != nums[n - 2]) {
            ret[i++] = nums[n - 1];
        }

      
        return ret;
    }
};

 方法二： 异或解法

*思路：

* 1. 只有两个元素出现一次,其它的元素都出现两次.

* 2. 全部元素异或消掉出现两次的数字. 异或的结果为s.

* 3. 寻找s的lowbit值. lowbit(s)为s的二进制表达式中最右边的1所对应的值. 因此lowbit(s)二进制表达式中只有一个bit 1.   lowbit(s) = s & -s （找到异或结果的最低位为1的位置）

* 4. 用lowbit(s)将数组分成两组. 一组中,元素A[i] & lowbit(s) == lowbit(s), 

   即包含lowbit(s)的bit 1. 剩余的是另一组.而且,两个不同数也一定分在不同组. 因为异或值s中的bit1就是   因为两个数字的不同而贡献的.

* 5. 同一组的元素再异或求出不同数字. 出现两次的数字, 肯定出现同一组, 异或后消除掉.

class Solution 
{
public:
  vector<int> singleNumber(vector<int>& nums) 
  {
    const int N=nums.size();
    int s = 0;
    for(auto x : nums)
    {
      s ^=x;
    }
    //防止溢出
    int lowbit = (s==INT_MIN?s:s & -s);
    int a=0,b=0;
    for(auto x:nums)
    {
      if((x & lowbit) == lowbit)
      {
        a^=x;
      }
      else
      {
        b^=x;
      }
    }
    return vector<int>{a,b};
  }
};

以2和3为例子： 

如果还是不懂的话，建议自己用具体的数来模拟一下它的过程。比如像我上图一样。

好了，本次分享就到这里了，希望我们对异或的知识用法有很深的认识。

最后，到了本次鸡汤环节：

下图文字与大家共勉！