数据结构——第二讲、线性结构（线性表及其实现）

本文介绍了一元多项式的表示方法，并通过线性表的不同实现方式详细讲解了多项式的加法、乘法等运算过程。同时，还探讨了线性表的基本概念、存储结构及其操作方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2.1 线性表及其实现

线性表有不同的实现（数组实现的线性表，和链表实现的线性表），也有一些扩展（链表实现里面有多重链表（用这个多重链表表示稀疏矩阵比较合适），也就是链表中的元素不光是单个元素，也有可能是另一个多重链表，当然，还包括双向链表，循环链表）

2.1.1 多项式的表示

一元多项式
$f(x)=a_{0}+a_{1}x+a_{2}x^{2}+\cdot \cdot \cdot + a_{n}x^{n}$
对它进行的操作有：相加、相减、相乘等，有多种方式表示。

方法1： 顺序存储结构直接表示。用一个数组存储多项式，数组的值为多项式的系数，数组的下标为多项式每项的指数。显然，这样的方式虽然简单也便于运算，但是会造成数组空间的巨大浪费。
方法2： 顺序存储结构表示非零项。用数组只存非零项，那么数组的值就不可以只有系数，它应该同时包含它的系数和指数，所以可以用结构数组来存储。
这样存储如果想要方便的运算，那么就必须将指数按顺序存储。
方法2表示多项式实例
（图片来源：中国大学MOOC浙江大学数据结构）

下面是求和的代码，刚开始的时候把p3设成局部变量，想返回p3又返回不了数组，只能把p3的地址返回回来，结果就返回了个地址，算出来的数字存在p3里面全内存一收回啥都没了，还奇怪为什么只能输出一个正确数字，debug的时候看见地址没变数据变了才知道怎么回事，麻个鸡。

Java代码

public class Main {
    public static void main(String[] args) {
        Struct[] x1 = {
                new Struct(9, 12),
                new Struct(15, 8),
                new Struct(3, 2)
        };
        Struct[] x2 = {
                new Struct(26, 19),
                new Struct(-4, 8),
                new Struct(-13, 6),
                new Struct(82, 0)
        };
        sum(x1, x2, x1.length, x2.length);
    }

    static class Struct {
        int coefficient = 0;
        int exponent = 0;

        Struct() {
        }

        Struct(int coefficient, int exponent) {
            this.coefficient = coefficient;
            this.exponent = exponent;
        }
    }

    //思路：把这两个多项式看成队列，排好队，只看这两队最前面的两个人，
    //比较这两个人，只有两种情况（相等或者不相等），
    //相等的：两个排头的同时出队合体，
    //不相等的：把大的那个人出队，
    //（这里隐藏的条件是两个多项式，指数从大到小排列，最前面的那一项都是各自的多项式里最大的，如果他们不相等，那么比较大的那个肯定没有和它相同的项了，所以可以直接出队）
    private static void sum(Struct[] x1, Struct[] x2, int length1, int length2) {
        //定义两个指向数组的指针，
        int index1 = 0, index2 = 0;
        //定义一个结果数组指针和一个结果数组
        Struct[] result = new Struct[length2 * 2];
        int index = 0;
        //只要有一个指针走完了那就结束了，要把剩下的那一队后面的全接过来
        while (index1 < length1 && index2 < length2) {
            //如果指数相等就同时出队
            result[index] = new Struct();
            if (x1[index1].exponent == x2[index2].exponent) {
                result[index].exponent = x1[index1].exponent;
                result[index++].coefficient = x1[index1++].coefficient + x2[index2++].coefficient;
            }
            //否则把大的出队，这里可以写一个函数专门处理出队，指针加1的操作，但是感觉意义不大
            else if (x1[index1].exponent > x2[index2].exponent) {
                //出x1
                result[index].exponent = x1[index1].exponent;
                result[index++].coefficient = x1[index1++].coefficient;
            } else {
                //出x2
                result[index].exponent = x2[index2].exponent;
                result[index++].coefficient = x2[index2++].coefficient;
            }
        }
        //看看是哪个走完了
        if (index1 == length1 && index2 != length2) {
            for (; index2 < length2; index2++) {
                result[index++] = x2[index2];
            }
        }else if (index1 != length1 && index2 == length2){
            for (; index1 < length1; index1++) {
                result[index++] = x2[index1];
            }
        }
        for (Struct struct : result) {
            System.out.println(struct.coefficient + "--" +struct.exponent);
        }

    }
}

C代码

//定义全局变量、结构体、声明函数
struct Polynomial
{
	int coefficient = 0;
	int exponent = 0;
}p1[100], p2[100], p3[100]，p4[100];

int index = 0;

int Sum(Polynomial p1[], Polynomial p2[],int num1,int num2);
//求和函数本体
int Sum(Polynomial p1[], Polynomial p2[], int num1, int num2) {
	int index1 = 0, index2 = 0;
	while (index1 < num1||index2 < num2) {
		if (p1[index1].exponent > p2[index2].exponent) {
			p3[index] = p1[index1];
			index1++;
			index++;
		}
		else if (p1[index1].exponent == p2[index2].exponent) {
			p3[index].coefficient = p1[index1].coefficient + p2[index2].coefficient;
			if (p3[index].coefficient)p3[index].exponent = p1[index1].exponent;
			index1++;
			index2++;
			index++;
		}
		else {
			p3[index] = p2[index2];
			index2++;
			index++;
		}
		if (index1 >= num1) {
			for (; index2 < num2; index2++) {
				p3[index] = p2[index2];
				index++;
			}
		}
		if (index2 >= num2) {
			for (; index1 < num1; index1++) {
				p3[index] = p2[index1];
				index++;
			}
		}
	}
	return 0;
}

求和的思路是这样的，把按从大到小的顺序存储的多项式从第一项开始比较他们的指数，指数大的记下来然后看下一个，小的保持不变，指数相等的相加，同时向后看，当有一个多项式加完的时候，把剩下的那个接在结尾即可。

下面附上求乘积的代码。

//先挨个乘完，然后从大到小排序，然后把重复的合并同类项，整理到p4的时候把系数为零的跳过即可。
int multiply(Polynomial p1[], Polynomial p2[], int num1, int num2) {
	for(int i = 0;i<num1;i++)
		for (int j = 0; j < num2; j++) {
			p3[index].coefficient = p1[i].coefficient*p2[j].coefficient;
			p3[index].exponent = p1[i].exponent + p2[j].exponent;
			index++;
		}

	for(int i= num1*num2-1;i>0;i--)
		for (int j = 0; j < i; j++) {
			if (p3[i].exponent > p3[j].exponent) {
				//借用p4[0]作为中间变量完成交换
				p4[0] = p3[i];
				p3[i] = p3[j];
				p3[j] = p4[0];
			}
		}
	//接下来合并同类项
	for (int i = 0; i < num1*num2-1; i++) {
		if (p3[i].exponent == p3[i + 1].exponent) {
			p3[i].coefficient = p3[i].coefficient + p3[i+1].coefficient;
			p3[i + 1].coefficient = 0;
		}
	}
	//整理结果
	index = 0;
	for (int i = 0; i < num1*num2; i++) {
		if (p3[i].coefficient != 0) {
			p4[index] = p3[i];
			index++;
		}
	}
	return 0;
}

方法3： 链表结构存储非零项，就是在方法2的结构体中加一个指针域，让它指向下一个结构体。

//C++代码，如果用c语言需要
//typedef struct PolyNode *Polymial
//Polymial link;
struct PolyNode
{
	int coefficient = 0;
	int exponent = 0;
	Polynomial *link;
}

2.1.2 线性表及存储结构
1、什么是线性表
同类型数据元素构成有序序列的线性结构。个数叫长度，没有元素时叫空表，起始位置叫表头，结束位置叫表尾。
2、线性表的抽象数据类型描述（想象成一个线性表类，包括数据和操作）
类型名称：线性表（List）
数据对象集：线性表是n（>=0）个元素构成的有序序列
操作集：L表示线性表，x表示元素，整数i表示位置，从1开始计算

List MakeEmpty()						//1、初始化一个空表
ElementType FindK(int K, List L)		//2、找线性表中的第K个元素并返回
int Find(ElementType x, List L)			//3、返回元素x在线性表L中的位置

void Insert(Element x, int i, List L)	//4、在第i个元素之前插入元素x
void Delete(int i,List L)				//5、删除第i个元素
int Length(list L)						//6、返回线性表的长度

3、线性表的存储方式
1）、顺序存储方式
利用数组连续存储，下标从0到n-1，存a1到an，线性表长度正好是最后一个元素的下标加1。

typedef struct LNode *List
struct LNode{
	ElementType Data[MAXSIZE];   //ElementType类型的数组存数据
	int last;                    //最后一个元素的下标
}L;						    	 //实例化一个线性表L
List PtrL;				    	 //或者一个LNode类型的指针
//L.Data[i]或PtrL->Date[i]，访问某一个元素
//L.last+1或PtrL->last+1，获得线性表长度

用上述顺序存储结构实现操作集的主要操作：

创建一个空链表，初始化，MakeEmpty()

//注意，List是上面定义的struct LNode *List，是一个结构体指针
List MakeEmpty()｛
	//声明一个LNode类型的指针
	List PtrL;
	
	//malloc表示分配特定长度的内存，按字节计，sizeof用来获取LNod类型所需空间
	//把PtrL指向这个申请好的空间
	PtrL = (List)malloc(sizeof(LNode));
	
	//把last设为-1，使长度为last+1=0
	Ptrl->last = -1;
	return PtrL;
｝

查找某个特定元素，Find()

int Find(ElementType x, List PtrL){
	for(int i = 0; i <= PtrL->last; i++){
		if(PtrL->Data[i] == x) return i;
	}
	return -1;
}

插入，Insert()

//每次都打PtrL太麻烦了，换成L吧……
void Insert(ElementTpye x, int i, List L){
	if(L->last==MAXSIZE-1){
		printf("表满！");
		return;
	}
	//不能在标号为0（即i为1）的位置前面再插，但是可以在last+1（即i为last+2）的位置插入，算添加一个元素。
	if(i<1 || i>L->last+2){
		printf(""位置不合法！);
		return;
	}
	//第i个元素的下标是i-1，把i-1的位置空出来给新元素
	for(int k = L->last; k>=i-1; k--){
		L->Data[k+1] = L->Data[k];
	}
	L->Data[i-1] = x;
	L->last++;
}

删除，Delete()，删除第i个元素（位置i-1）

void Delete(int i, List L){
	if(i<1 || i>L->last+1){
		printf("位置不存在");
		return;
	}
	for(int j = i-1; j<last; j++)
		L->Data[j] = L->Data[j+1];
	L->last--;
}

2）、链式存储方式（不需要物理上相邻）
每一个节点都是一个结构体，顺序存储每一个链表是一个结构体

typedef struct LNode *List
struct LNode(){
	ElementType Data;
	List NEXT;
}
struct LNode L;
List PtrL;

求表长，Length()

int Length(List PtrL){
	int j = 0;
	List p = PtrL;
	while(p){          //p为NULL时，循环会退出
		p=p->NEXT;
		j++;
	}
	return j;
}

序号K查找，FindK()

List FindK(int K, List PtrL){
	List p = PtrL;
	int i = 1;
	while(p != NULL && i < K){
		p = p->NEXT;
		i++;
	}
	if(i == K)
		return p;
	else
		return NULL;
}

查找某个元素对应的节点（不是某个元素的序号），Find()

List Find(ElementType x, List PtrL){
	List p = PtrL;
	while(p != NULL && p->Data != x){
		p=p->NEXT;
	}
	return p;
}

插入Insert()，插在第i个位置，即插在第i-1个位置的后面

List Insert(ElementType x, int i, List PtrL){
	List p = (List)malloc(sizeof(struct LNode));
	p->Data = x;
	if(i == 1){
		p->NEXT = PtrL;
		return p;
	}
	s = FindK(i-1,PtrL);
	if(!s){
		printf("参数i错误");
		return NULL;
	}else{
		p->NEXT = s->NEXT;
		s->NEXT = p;
		return PtrL;
	}
}

删除Delete()，删除第i个节点

List Delete(int i, List PtrL){
	List p;
	if(i == 1){
		p = PtrL;
		if(PtrL!=NULL)
			PtrL = PtrL->NEXT;
		else
			return NULL;
		free(p);
		return PtrL;
	}
	p = FindK(i-1,PtrL);
	if(p == NULL || p->NEXT == NULL){
		printf("找不到参数");
		return NULL;
	}else{
		List s = p->NEXT;
		p->NEXT = s->NEXT;
		free(s);
		return PtrL;
	}
}

2.1.3 广义表与多重链表
这个多重链表先做到能理解它是怎么回事，用代码实现就得好好想想怎么搞了（一般都是遇到需要使用这个数据结构解决问题的时候才会想办法实现）……
广义表
广义表是一般线性表的推广，一般线性表中元素是基本元素，在广义表中，元素可以是基本元素也可以是另一个广义表。

typedef struct GNode *GList
struct GNode{
	int Tag;
	union{
		Elementtype Data;
		GList SubList;
	}URegion;
	GList NEXT;
}

多重链表
链表中的节点可能属于多个链表，有多个指针域。（双向链表不算多重链表）。
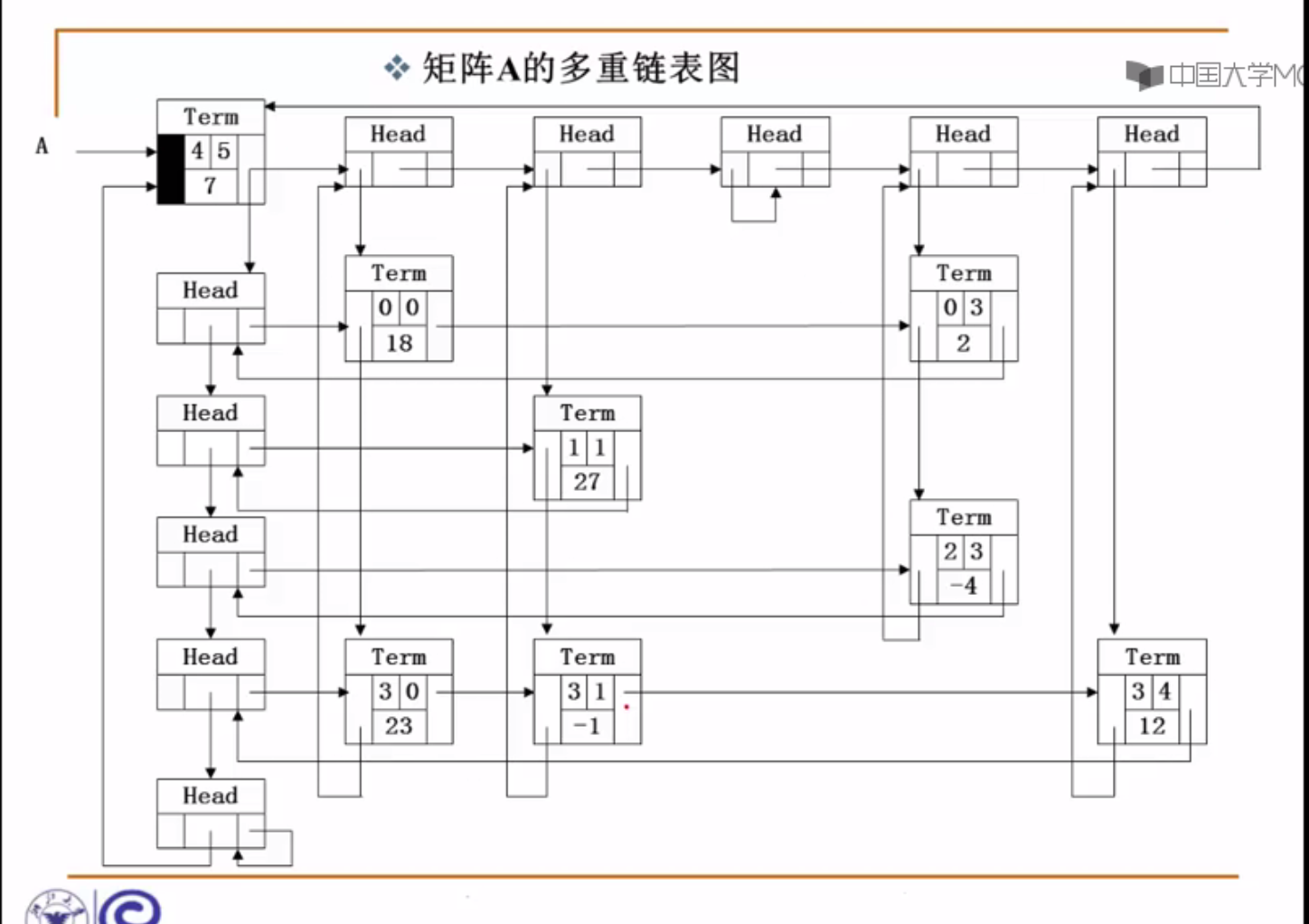
存储一个稀疏矩阵
这里写图片描述