彻底理解堆

什么是堆

在计算机科学中堆是一种很有趣的数据结构，实际上通常用数组来存储堆中的元素，但是我们却可以把数组中元素视为树，如图所示：

这就是一个普通的数组，但是我们可以将其看做如下图所示的树：

这是怎么做到的呢？

原来虽然我们是在数组中存储的堆元素，但是这里面有一条隐藏的规律，如果你仔细看上图就会发现：

• 每一个左子树节点的下标是父节点的2倍
• 每一个右子树节点的下标是父节点的2倍再加1

也就是说在数组中实际上隐藏了上面的这两条规律，如图所示：

堆这种数据结构最棒的地方在于我们无需像树一样存储左右子树的信息，而只需要通过下标运算就可以轻松的找到一个节点的左子树节点、右子树节点以及父节点，如下所示，相对于树这种数据结构来说堆更加节省内存。

int parent(int i){   // 计算给定下标的父节点 
    return i/2;
}
int left(int i){     // 计算给定下标的左子树节点
    return 2*i;
}
int right(int i){    // 计算给定下标的右子树节点 
    return 2*i+1;
}

除了上述数组下标上的规律以外，你还会发现堆中的每一个节点的值都比左右子树节点大，这被称为大根堆，即对于大根堆来说以下一定成立：

array[i] > array[left(i)] && array[i] > array[right(i)] == true

相应的如果堆中每个一节点的值都比左右子树节点的值小，那么这被称为小根堆，即对于小根堆来说以下一定成立：

array[i] < array[left(i)] && array[i] < array[right(i)] == true

以上就是堆这种数据结构的全部内容了。

那么接下来的问题就是，给定一个数组，我们该如何将数组中的值调整成一个堆呢？

 

如何在给定数组上创建堆

在这里我们以大根堆为例来讲解如何在给定数组上创建一个堆。

给定数组的初始状态如下图a所示，从图中我们看到除array[2]之外其它所有节点都满足大根堆的要求了，接下来我们要做的就是把array[2]也调整成为大根堆，那么该怎么调整呢？

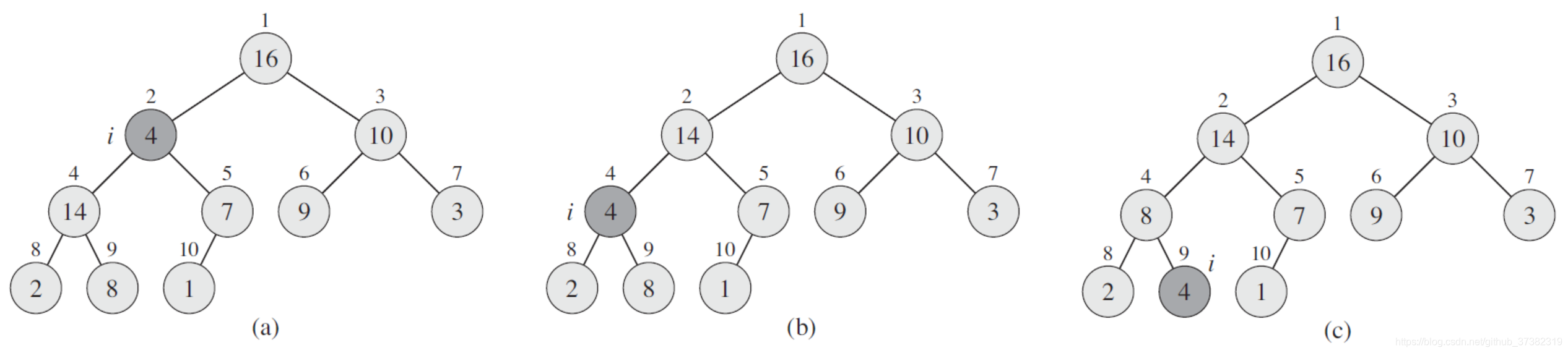
很简单，我们只需要将array[2]和其左右子树节点进行比较，最大的那个和array[2]进行交换，如图b所示，array[2]和其左子树array[4]以及右子树array[5]中最大的是array[4