algorithm-base：Morris遍历算法动画教程，空间复杂度O(1)的二叉树遍历
项目地址: https://gitcode.com/gh_mirrors/al/algorithm-base 你还在为二叉树遍历的空间复杂度发愁吗？递归遍历需要O(n)的栈空间，迭代法同样依赖栈或队列存储节点。今天我们将学习一种革命性的遍历技术——Morris遍历算法，它能实现O(1)空间复杂度的二叉树遍历，彻底摆脱对辅助数据结构的依赖。
读完本文你将掌握：
- Morris遍历的核心原理与优势
- 前序/中序/后序Morris遍历的实现差异
- 动画演示与代码实战（Java/Swift）
- 与传统遍历算法的性能对比分析
什么是Morris遍历？
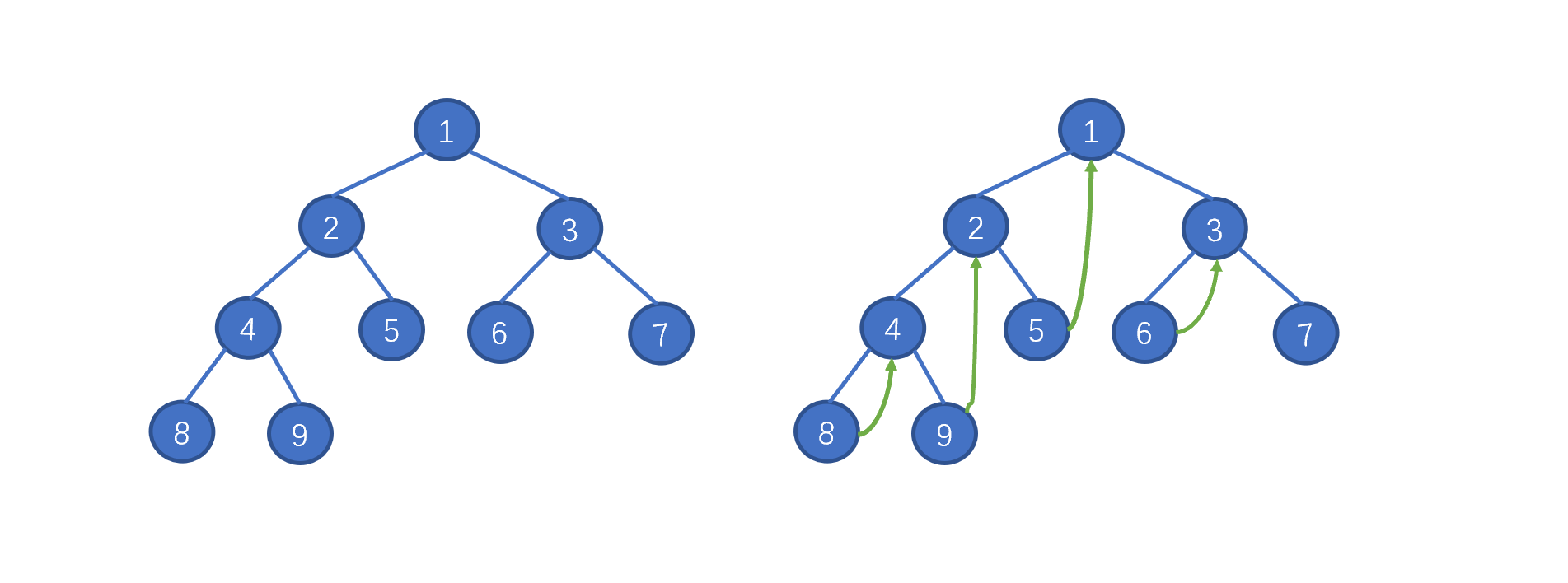
Morris遍历算法由J. H. Morris于1979年提出，其核心思想是利用二叉树中大量空闲的右指针，通过临时创建和删除指针的方式，实现对树的线性遍历。这种遍历方式不需要递归调用栈，也不需要手动维护辅助栈，从而将空间复杂度降至O(1)。
官方文档：二叉树基础
核心原理：线索二叉树技术
Morris遍历的本质是构建线索二叉树（Threaded Binary Tree），通过以下两个关键步骤实现遍历：
- 寻找前驱节点：对当前节点，找到其左子树的最右叶子节点（中序前驱）
- 创建/删除线索：
- 首次访问时创建线索（前驱节点右指针指向当前节点）
- 二次访问时删除线索（恢复树结构）
前序Morris遍历详解
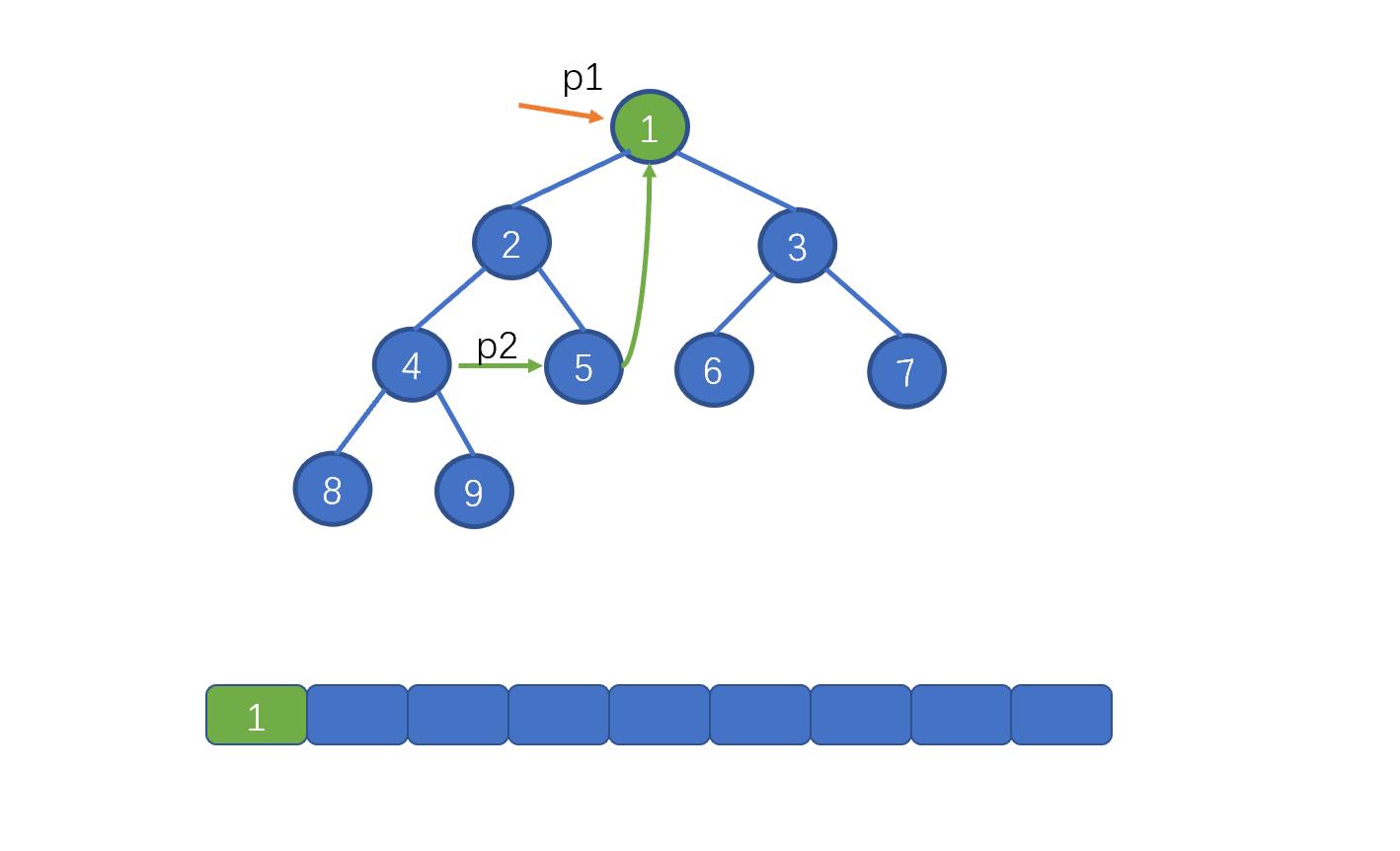
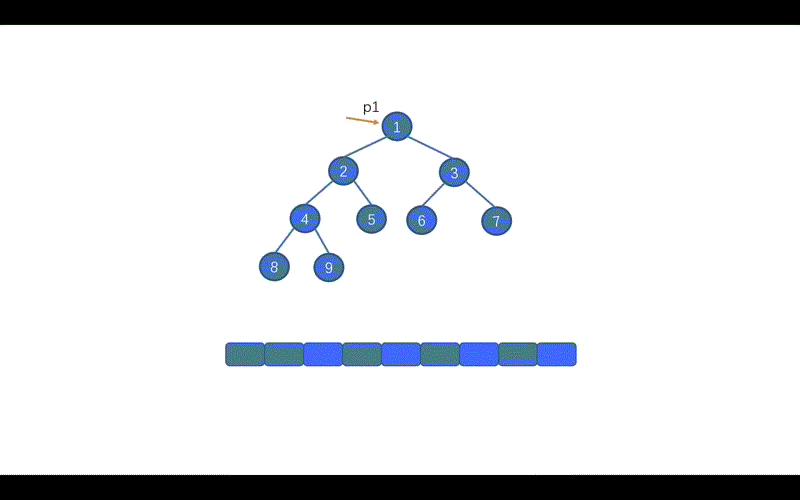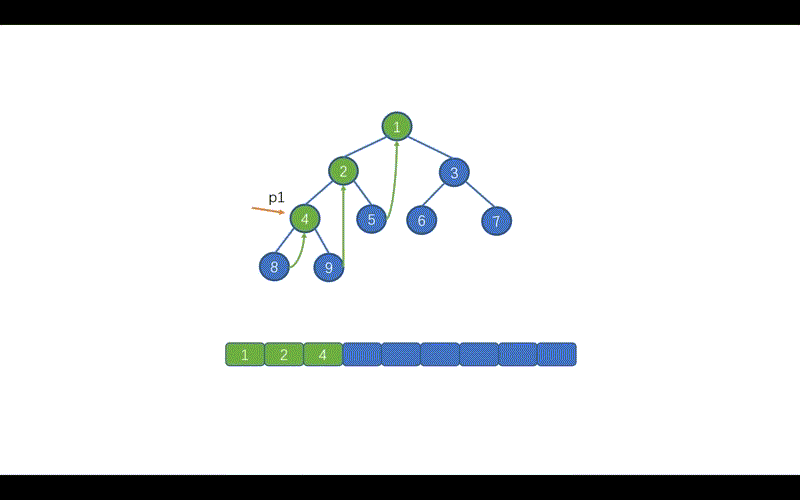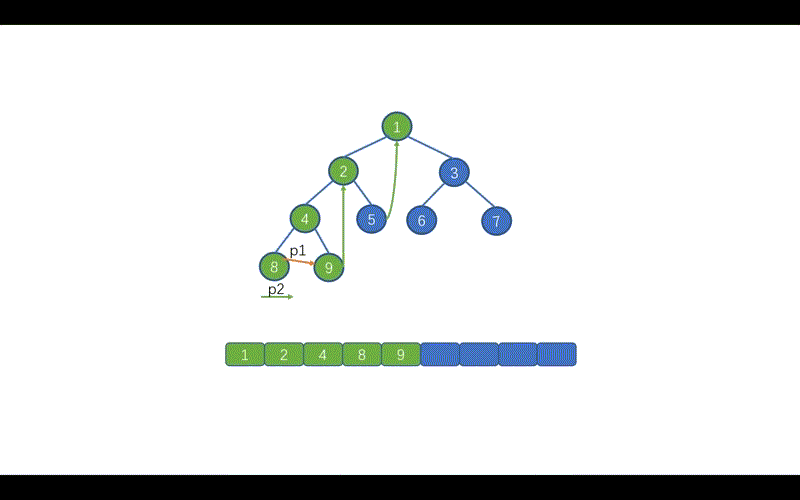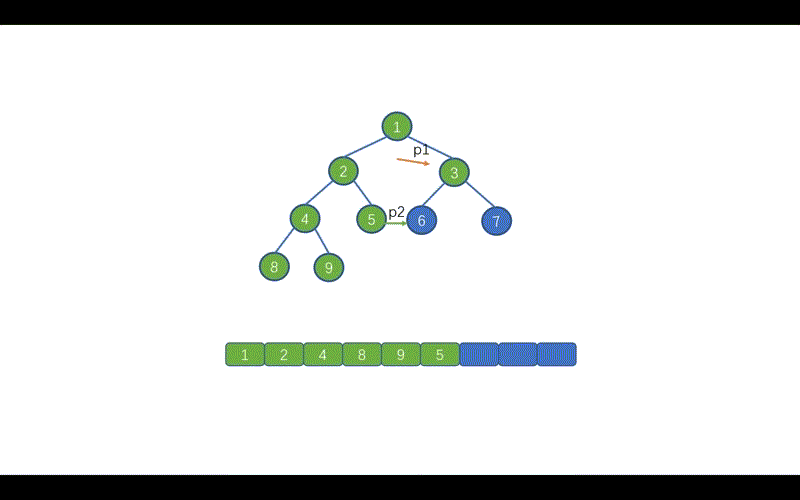
前序遍历（根→左→右）的Morris实现遵循以下规则：
- 若左子树为空，直接访问当前节点并向右移动
- 若左子树非空，找到左子树最右节点：
- 若未创建线索，访问当前节点并创建线索后向左移动
- 若已创建线索，删除线索后向右移动
动画演示
Java实现代码
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if (root == null) return list;
TreeNode p1 = root; // 当前节点指针
TreeNode p2 = null; // 前驱节点指针
while (p1 != null) {
p2 = p1.left;
if (p2 != null) {
// 找到左子树最右节点
while (p2.right != null && p2.right != p1) {
p2 = p2.right;
}
// 首次访问：创建线索并记录节点值
if (p2.right == null) {
list.add(p1.val); // 前序遍历：先访问根节点
p2.right = p1;
p1 = p1.left;
continue;
} else {
// 二次访问：删除线索
p2.right = null;
}
} else {
// 左子树为空，直接访问
list.add(p1.val);
}
p1 = p1.right; // 移动到右子树
}
return list;
}
}
完整代码：二叉树的前序遍历(Morris).md)
中序Morris遍历详解
中序遍历（左→根→右）与前序遍历的唯一区别在于节点值的访问时机：
- 前序遍历：首次访问节点时记录值
- 中序遍历：二次访问节点时记录值
动画对比
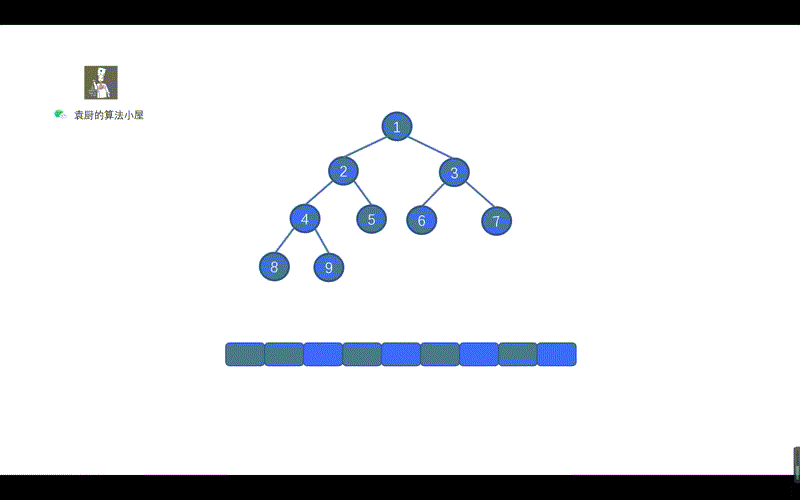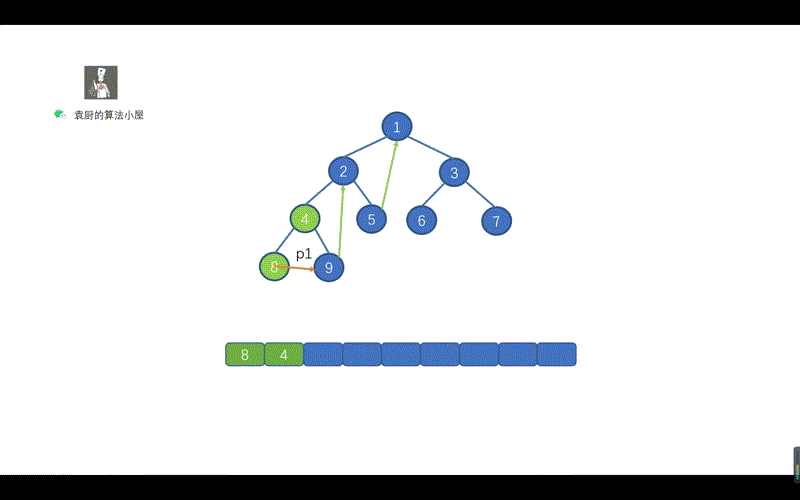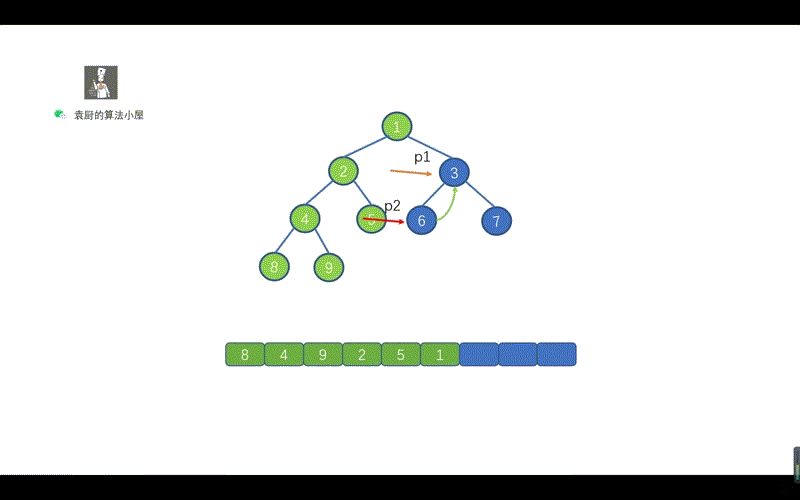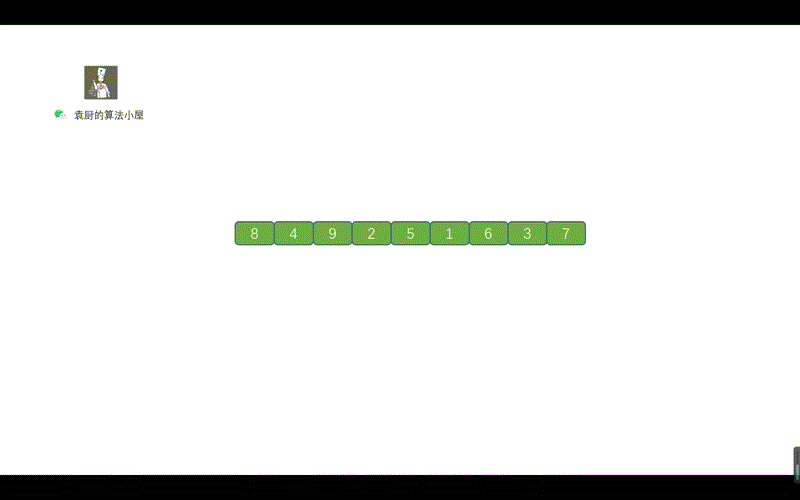
核心差异点
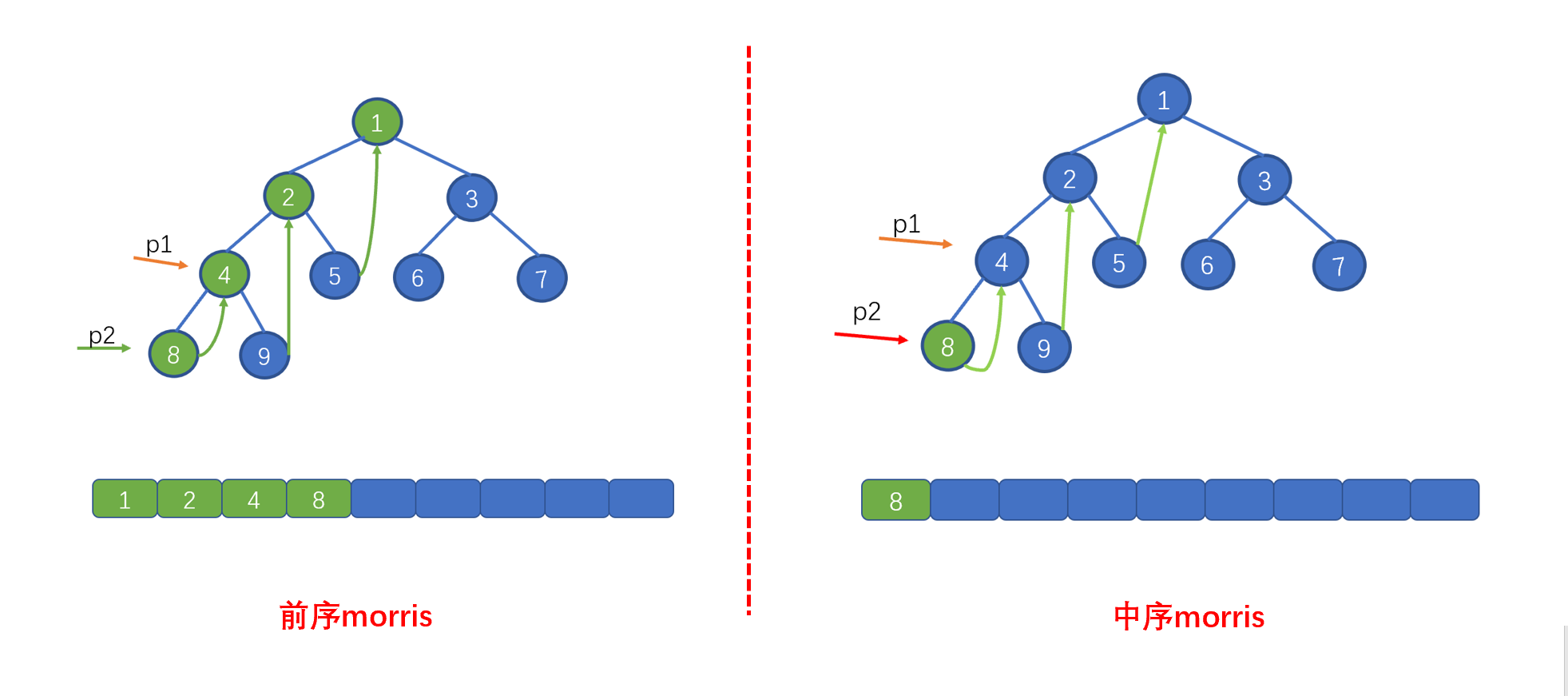
Swift实现代码
class Solution {
func inorderTraversal(_ root: TreeNode?) -> [Int] {
var list:[Int] = []
guard root != nil else { return list }
var p1 = root, p2: TreeNode?
while p1 != nil {
p2 = p1!.left
if p2 != nil {
// 找到左子树最右节点
while p2!.right != nil && p2!.right !== p1 {
p2 = p2!.right
}
if p2!.right == nil {
// 首次访问：创建线索
p2!.right = p1
p1 = p1!.left
continue
} else {
// 二次访问：删除线索并记录值（中序关键区别）
p2!.right = nil
}
}
list.append(p1!.val) // 中序遍历：此时访问根节点
p1 = p1!.right
}
return list
}
}
完整代码：二叉树中序遍历（Morris）
后序Morris遍历：进阶实现
后序遍历（左→右→根）是Morris遍历中最复杂的实现，需要通过逆序输出左子树右链的方式实现：
- 遍历过程与中序类似，但不直接记录节点值
- 当删除线索时，逆序输出当前节点左子树的右链
- 遍历结束后，单独处理根节点的右链
后序遍历特殊处理
public void postMorris(TreeNode root) {
// 1. 反转右链
TreeNode reverseNode = reverseList(root);
// 2. 遍历反转后的链表
TreeNode cur = reverseNode;
while (cur != null) {
list.add(cur.val);
cur = cur.right;
}
// 3. 恢复原链表结构
reverseList(reverseNode);
}
// 反转链表（右指针版）
public TreeNode reverseList(TreeNode head) {
TreeNode cur = head;
TreeNode pre = null;
while (cur != null) {
TreeNode next = cur.right;
cur.right = pre;
pre = cur;
cur = next;
}
return pre;
}
完整代码：二叉树的后续遍历（Morris）
三种遍历方式对比
| 遍历方式 | 访问时机 | 核心特点 | 动画演示 |
|---|---|---|---|
| 前序 | 创建线索时访问根节点 | 实现最简单，直接记录 | |
| 中序 | 删除线索时访问根节点 | 应用最广泛（如BST排序） | |
| 后序 | 逆序访问左子树右链 | 需要额外反转操作，实现复杂 | 二叉树的后续遍历（Morris） |
性能分析与应用场景
复杂度对比
| 遍历方式 | 时间复杂度 | 空间复杂度 | 适用场景 |
|---|---|---|---|
| 递归遍历 | O(n) | O(h) | 代码简洁，树高较小时 |
| 迭代遍历 | O(n) | O(h) | 避免栈溢出，树高较大时 |
| Morris | O(n) | O(1) | 内存受限环境，大数据量处理 |
注：h为树的高度，最坏情况下（斜树）h=n
实际应用建议
- 算法竞赛：优先使用Morris遍历优化空间敏感问题
- 工程实现：递归遍历代码更易维护，Morris适用于内存受限场景
- 面试场景：掌握Morris遍历能显著提升竞争力，体现对算法本质的理解
总结与学习资源
Morris遍历算法通过巧妙利用树的空闲指针，实现了空间复杂度O(1)的二叉树遍历，是算法优化的典范。掌握这一技术需要重点理解：
- 线索二叉树的构建与恢复过程
- 三种遍历方式的访问时机差异
- 后序遍历中的链表反转技巧
学习路线推荐：二叉树基础 → Morris前序 → Morris中序 → Morris后序
如果需要获取完整代码和更多动画演示，可以通过以下方式获取项目：
git clone https://gitcode.com/gh_mirrors/al/algorithm-base
希望本文能帮助你彻底掌握这一优雅的遍历算法！如果觉得有用，请点赞收藏，关注作者获取更多算法动画教程。
创作声明：本文部分内容由AI辅助生成（AIGC），仅供参考
