3种高效定位方案：二叉搜索树目标节点深度遍历策略
项目地址: https://gitcode.com/GitHub_Trending/le/LeetCode-Book 在二叉搜索树（Binary Search Tree, BST）中定位目标节点是算法面试高频考点。本文基于GitHub_Trending/le/LeetCode-Book项目中的经典题型，详解中序遍历倒序、迭代剪枝和morris遍历三种策略，结合剑指 Offer 54. 二叉搜索树的第 k 大节点和LCR 174. 寻找二叉搜索树中的目标节点实战案例，帮助开发者掌握O(1)空间复杂度的最优解。
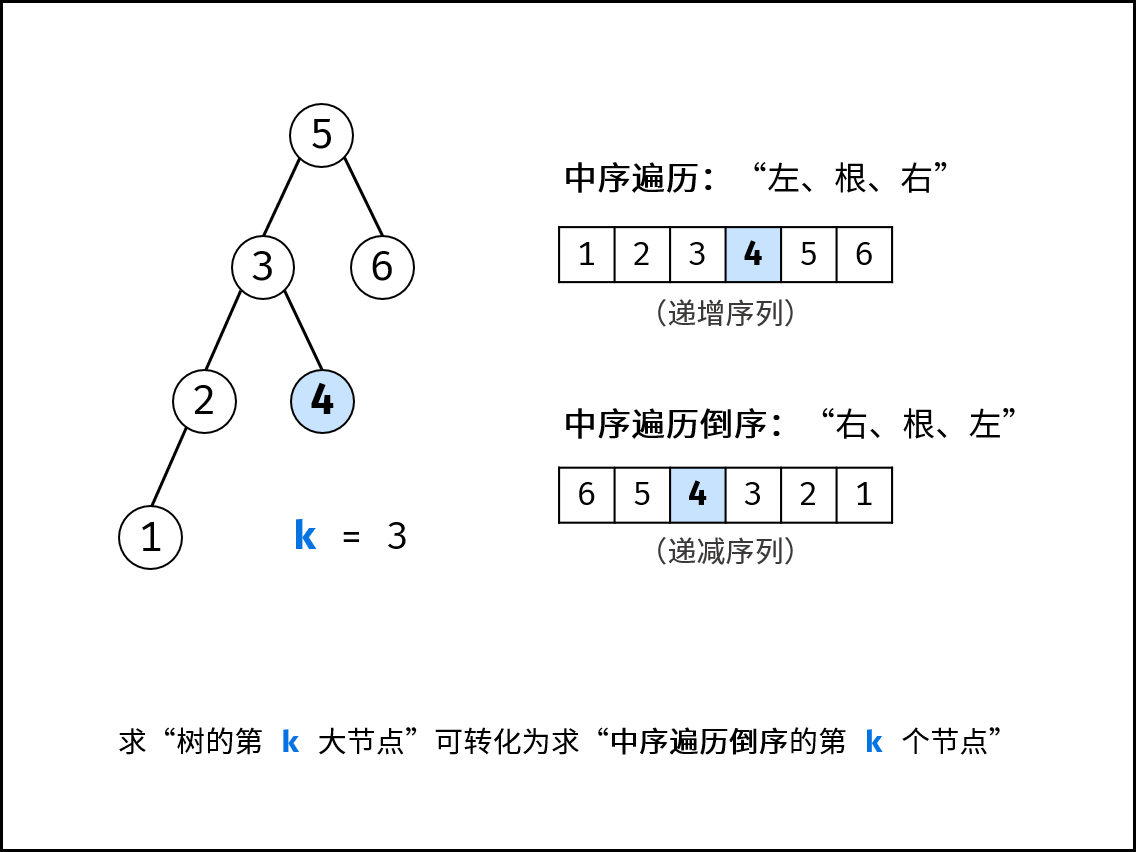
中序遍历倒序：递归实现（推荐新手）
二叉搜索树的中序遍历序列具有递增特性，其倒序（右-根-左）则为递减序列。通过递归遍历计数，可在第k次访问时直接返回目标节点值。
核心步骤
- 递归遍历右子树
- 访问当前节点并计数
- 计数达标时记录结果并剪枝
- 递归遍历左子树
代码实现
class Solution:
def kthLargest(self, root: TreeNode, k: int) -> int:
def dfs(root):
if not root: return
dfs(root.right) # 右
if self.k == 0: return
self.k -= 1 # 计数
if self.k == 0: self.res = root.val # 记录结果
dfs(root.left) # 左
self.k = k
dfs(root)
return self.res
上述代码来自剑指 Offer 54题解，通过类变量self.k实现跨递归调用的计数功能，当计数减至0时立即返回结果，避免无效遍历。
迭代剪枝：空间优化方案
递归实现虽然简洁，但存在栈溢出风险。迭代版本使用显式栈模拟递归过程，可在找到目标节点后立即终止遍历，平均空间复杂度优化至O(h)（h为树高）。
算法框架
public int kthLargest(TreeNode root, int k) {
Stack<TreeNode> stack = new Stack<>();
TreeNode curr = root;
while (curr != null || !stack.isEmpty()) {
// 遍历至最右节点
while (curr != null) {
stack.push(curr);
curr = curr.right;
}
curr = stack.pop();
if (--k == 0) return curr.val; // 计数剪枝
curr = curr.left;
}
return -1;
}
该实现参考LCR 174题解，通过栈结构手动维护遍历路径，适用于节点数较多的大型BST场景。
Morris遍历：O(1)空间突破
Morris遍历算法通过修改树的右指针实现线索化，彻底摆脱对栈/队列的依赖，实现常数级空间复杂度。在BST目标节点查找中，其时间复杂度仍保持O(n)，但内存占用显著降低。
算法流程图
关键步骤
- 初始化当前节点为根节点
- 无右子树时访问当前节点并移至左子树
- 有右子树时：
- 找到右子树最左节点（中序前驱）
- 未建立线索则建立线索并移至右子树
- 已建立线索则访问当前节点并恢复树结构
实战对比与选型建议
| 算法 | 时间复杂度 | 空间复杂度 | 适用场景 | 代码难度 |
|---|---|---|---|---|
| 递归遍历 | O(n) | O(n) | 小规模树/教学场景 | ★☆☆☆☆ |
| 迭代遍历 | O(n) | O(h) | 中等规模树/工程实现 | ★★☆☆☆ |
| Morris遍历 | O(n) | O(1) | 大数据量/内存受限 | ★★★★☆ |
项目资源索引
- 完整题解集合：sword_for_offer/docs/
- 迭代实现代码：LCR 174题解
- 复杂度分析：# 1.2 算法复杂度.md
掌握BST目标节点定位技术，不仅能应对剑指 Offer 54这类经典题型，更能为理解红黑树、B+树等高级数据结构奠定基础。建议结合# 0.1 刷题建议.md中的"刻意练习法"，通过不同难度的题目组合训练，达到在15分钟内写出最优解的面试要求。
创作声明：本文部分内容由AI辅助生成（AIGC），仅供参考
