快速选择算法终极指南：如何高效找出数组中的第K个最大元素
项目地址: https://gitcode.com/gh_mirrors/al/algorithm-base 想要快速找到数组中第K个最大元素吗？快速选择算法正是解决这个问题的完美方案！作为基于快速排序思想的优化算法，快速选择能在平均O(n)时间复杂度内完成任务，特别适合处理海量数据中的Top K问题。本文将用动画图解的方式，带你轻松掌握这个高效算法的精髓。
🔍 什么是快速选择算法？
快速选择算法是一种在未排序数组中查找第K小或第K大元素的高效算法。它继承了快速排序的分治思想，但通过巧妙优化避免了不必要的递归调用，从而大幅提升效率。
算法核心思想：
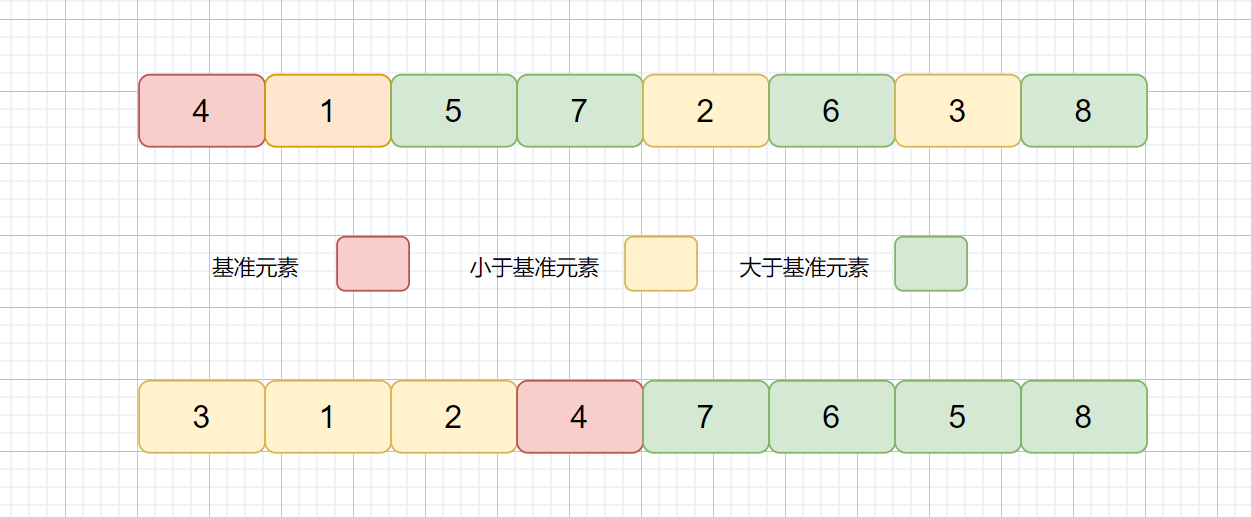
- 选择一个基准元素（pivot）
- 将数组分成三部分：小于、等于、大于基准元素
- 根据K值所在区间，只在相关部分继续搜索
⚡ 快速选择 vs 快速排序：性能大比拼
虽然快速选择脱胎于快速排序，但两者在目标上有着本质区别：
| 算法 | 目标 | 时间复杂度 | 应用场景 |
|---|---|---|---|
| 快速排序 | 完全排序整个数组 | O(n log n) | 需要完整排序时 |
| 快速选择 | 只找特定位置的元素 | O(n) | 找中位数、Top K等 |
🎯 快速选择算法实战步骤
第一步：选择基准元素
使用"三数取中法"选择基准元素，避免最坏情况的发生：
int mid = low + ((high - low) >> 1);
if (nums[low] > nums[high]) swap(nums, low, high);
if (nums[mid] > nums[high]) swap(nums, mid, high);
if (nums[mid] > nums[low]) swap(nums, mid, low);
第二步：分区操作
将数组重新排列，使所有小于基准的元素位于其左侧，大于基准的元素位于其右侧。
第三步：递归选择
根据K值的位置决定下一步搜索方向：
- 如果K在左分区：只在左半部分继续搜索
- 如果K在右分区：只在右半部分继续搜索
- 如果K在当前基准位置：直接返回结果
🚀 快速选择算法优势详解
时间复杂度优势：
- 平均情况：O(n)
- 最坏情况：O(n²)
- 最好情况：O(n)
空间复杂度：
- 平均情况：O(log n)
- 最坏情况：O(n)
💡 实际应用场景
1. 找中位数
当K等于n/2时，快速选择算法能快速找到数组的中位数。
2. 求Top K元素
结合快速选择，可以高效找出数组中前K大的元素。
3. 统计数据分析
在数据分析中，经常需要找到特定分位数的值。
🔧 优化技巧与最佳实践
三数取中法
避免选择最大或最小值作为基准，保证算法性能稳定。
与插入排序结合
当子数组长度较小时，切换到插入排序，提高整体效率。
处理重复元素
使用三向切分技术，将数组分成小于、等于、大于基准的三部分，减少递归深度。
📊 性能对比分析
🎉 总结
快速选择算法是解决"数组中第K个最大元素"问题的利器！通过分治思想和巧妙优化，它能在保持代码简洁的同时，提供卓越的性能表现。无论你是准备技术面试，还是在日常开发中遇到类似问题，掌握这个算法都将让你事半功倍。
记住：选择合适的基准元素 + 只在必要部分递归搜索 = 高效解决问题 🎯
掌握快速选择算法，让你的编程技能更上一层楼！
创作声明：本文部分内容由AI辅助生成（AIGC），仅供参考
