算法性能优化技巧！algorithm-base解析时间与空间复杂度的平衡
项目地址: https://gitcode.com/gh_mirrors/al/algorithm-base 你是否还在为算法超时问题烦恼？是否遇到过"时间超限"或"内存溢出"的错误提示？本文将通过algorithm-base项目中的经典案例，带你掌握时间复杂度（Time Complexity）与空间复杂度（Space Complexity）的平衡技巧，让你的算法既快又省！
读完本文你将学到：
- 如何通过排序算法案例分析复杂度权衡
- 时间换空间与空间换时间的实用策略
- 基于实际场景的复杂度优化技巧
- 常见算法复杂度对比与选择指南
复杂度基础：算法效率的度量衡
算法复杂度是评估算法性能的重要指标，包括时间复杂度和空间复杂度。时间复杂度描述算法执行时间与输入规模的关系，空间复杂度描述算法所需存储空间与输入规模的关系。
在algorithm-base项目的数据结构和算法/冒泡排序.md中详细介绍了复杂度分析方法：
- 时间复杂度常用大O符号表示，如O(n)、O(n²)、O(logn)
- 空间复杂度同样使用大O符号，如O(1)、O(n)、O(n²)
- 分析时需考虑最好、最坏和平均情况
时间换空间：冒泡排序的优化之路
冒泡排序是最基础的排序算法之一，其基本思想是通过两两比较相邻元素并交换位置，使大的元素"冒泡"到数组末端。
原始冒泡排序实现
public int[] sortArray(int[] nums) {
int len = nums.length;
for (int i = 0; i < len; ++i) {
for (int j = 0; j < len - i - 1; ++j) {
if (nums[j] > nums[j+1]) {
swap(nums,j,j+1);
}
}
}
return nums;
}
原始实现的时间复杂度为O(n²)，空间复杂度为O(1)。但即使数组已经有序，算法仍会执行完整的循环。
优化一：添加标志位
通过添加标志位判断是否发生交换，当数组有序时提前退出：
public int[] sortArray(int[] nums) {
int len = nums.length;
boolean flag = true; // 标志位
for (int i = 0; i < len && flag; ++i) {
flag = false; // 重置标志位
for (int j = 0; j < len - i - 1; ++j) {
if (nums[j] > nums[j+1]) {
swap(nums,j,j+1);
flag = true; // 发生交换，置为true
}
}
}
return nums;
}
优化后，最好情况下（数组已排序）的时间复杂度降至O(n)，空间复杂度仍为O(1)。
| 算法版本 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 是否稳定 |
|---|---|---|---|---|---|
| 原始版 | O(n²) | O(n²) | O(n²) | O(1) | 稳定 |
| 优化版 | O(n) | O(n²) | O(n²) | O(1) | 稳定 |
空间换时间：快速排序的性能飞跃
快速排序采用分治思想，通过选择基准元素将数组分区，递归处理子区间。在数据结构和算法/快速排序.md中详细介绍了其实现与优化。
快速排序基本实现
public void quickSort(int[] nums, int low, int high) {
if (low < high) {
int index = partition(nums,low,high);
quickSort(nums,low,index-1);
quickSort(nums,index+1,high);
}
}
public int partition(int[] nums, int low, int high) {
int pivot = nums[low]; // 选择第一个元素作为基准
int start = low;
while (low < high) {
while (low < high && nums[high] >= pivot) high--;
while (low < high && nums[low] <= pivot) low++;
if (low >= high) break;
swap(nums, low, high);
}
swap(nums,start,low); // 基准值归位
return low;
}
快速排序的平均时间复杂度为O(nlogn)，但最坏情况下（数组有序）会退化为O(n²)，空间复杂度为O(logn)（递归栈空间）。
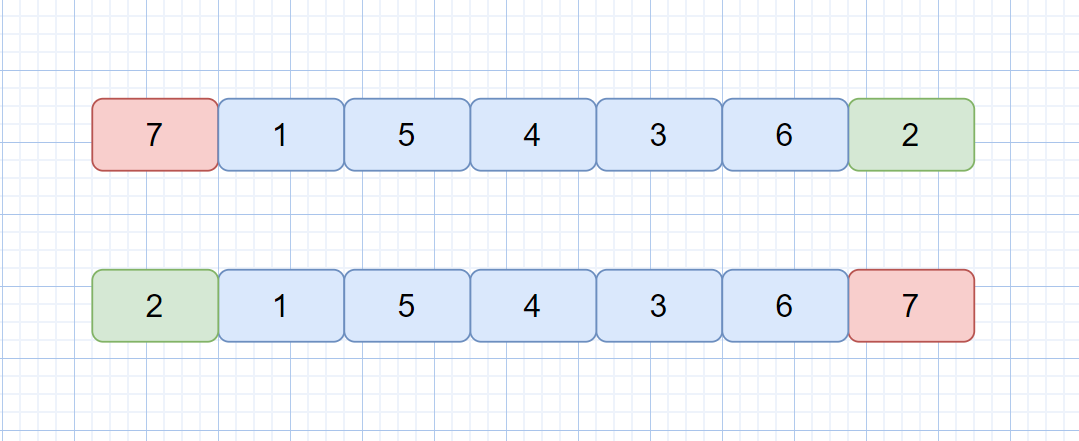
优化策略：三数取中法
通过选择三个位置元素的中间值作为基准，避免最坏情况：
// 三数取中法选择基准
int mid = low + ((high-low) >> 1);
if (nums[low] > nums[high]) swap(nums,low,high);
if (nums[mid] > nums[high]) swap(nums,mid,high);
if (nums[mid] > nums[low]) swap(nums,mid,low);
// 此时nums[low]为中间值，作为基准
复杂度平衡实战技巧
1. 小规模数据使用插入排序
当数据规模较小时（通常n≤7），插入排序效率可能高于快速排序。algorithm-base项目中采用了混合策略：
private static final int INSERTION_SORT_MAX_LENGTH = 7;
public void quickSort(int nums[], int low, int high) {
// 小规模数据使用插入排序
if (high - low <= INSERTION_SORT_MAX_LENGTH) {
insertSort(nums,low,high);
return;
}
// 快速排序逻辑...
}
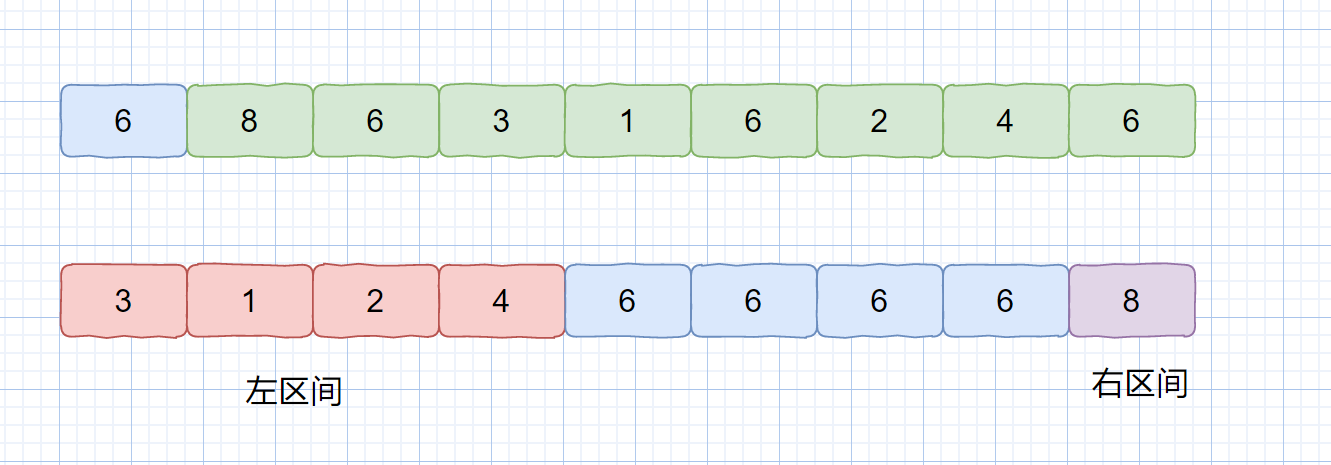
2. 三向切分处理重复元素
对于含大量重复元素的数组，三向切分可将数组分为小于、等于和大于基准的三部分，减少递归区间：
// 三向切分实现
int left = low, i = low + 1, right = high;
int pivot = nums[low];
while (i <= right) {
if (pivot < nums[i]) {
swap(nums,i,right);
right--;
} else if (pivot == nums[i]) {
i++;
} else {
swap(nums,left,i);
left++;
i++;
}
}
quickSort(nums,low,left-1); // 排序小于基准的部分
quickSort(nums,right+1,high); // 排序大于基准的部分
3. 迭代实现替代递归
递归可能导致栈溢出，可使用栈模拟递归实现快速排序：
public int[] sortArray(int[] nums) {
Stack<Integer> stack = new Stack<>();
stack.push(nums.length - 1);
stack.push(0);
while (!stack.isEmpty()) {
int low = stack.pop();
int high = stack.pop();
if (low < high) {
int index = partition(nums, low, high);
stack.push(index - 1);
stack.push(low);
stack.push(high);
stack.push(index + 1);
}
}
return nums;
}
常见算法复杂度对比与选择
algorithm-base项目提供了丰富的算法实现，以下是常见排序算法的复杂度对比：
| 算法名称 | 最好时间复杂度 | 最坏时间复杂度 | 平均时间复杂度 | 空间复杂度 | 是否稳定 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n²) | O(n²) | O(1) | 稳定 |
| 快速排序 | O(nlogn) | O(n²) | O(nlogn) | O(logn) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
选择建议：
- 数据量小且基本有序：冒泡排序（优化版）
- 一般情况：快速排序（优化版）
- 稳定性要求高：归并排序
- 空间限制严格：堆排序
总结与展望
算法优化是时间复杂度与空间复杂度的平衡艺术。通过algorithm-base项目中的经典案例，我们学习了如何通过标志位、三数取中、混合排序等技巧优化算法性能。
实际开发中，建议：
- 先实现基础版本，确保正确性
- 使用复杂度分析工具定位瓶颈
- 针对性应用优化技巧，避免过早优化
- 结合具体场景选择合适算法
项目完整代码可通过以下仓库获取：https://gitcode.com/gh_mirrors/al/algorithm-base
掌握复杂度平衡技巧，让你的算法在效率与资源占用间找到最佳平衡点！
创作声明：本文部分内容由AI辅助生成（AIGC），仅供参考
