深入理解Halfrost-Field中的PCA与降维技术
引言
在机器学习和数据分析领域,我们经常会遇到高维数据的处理问题。高维数据不仅增加了计算复杂度,还可能包含大量冗余信息。本文将深入探讨主成分分析(PCA)这一经典降维技术,帮助读者理解其原理、应用场景及实现方法。
一、为什么需要降维?
1.1 高维数据的挑战
在实际应用中,我们往往希望使用尽可能多的特征来提高模型的准确性,特别是在图像处理等领域,高维特征几乎是不可避免的。然而,高维特征会带来以下几个主要问题:
- 计算效率下降:特征维度越高,模型训练所需的时间和计算资源就越多
- 可解释性降低:当特征数量过多时,很难直观理解每个特征的实际含义
- 特征冗余:不同特征之间可能存在高度相关性,如厘米和英尺都能表示长度
1.2 降维的基本思想
降维的核心目标是将高维特征投影到低维空间,同时尽可能保留原始数据的重要信息。如下图所示,我们可以将二维特征投影到一条绿色直线上,从而将特征从二维降为一维:
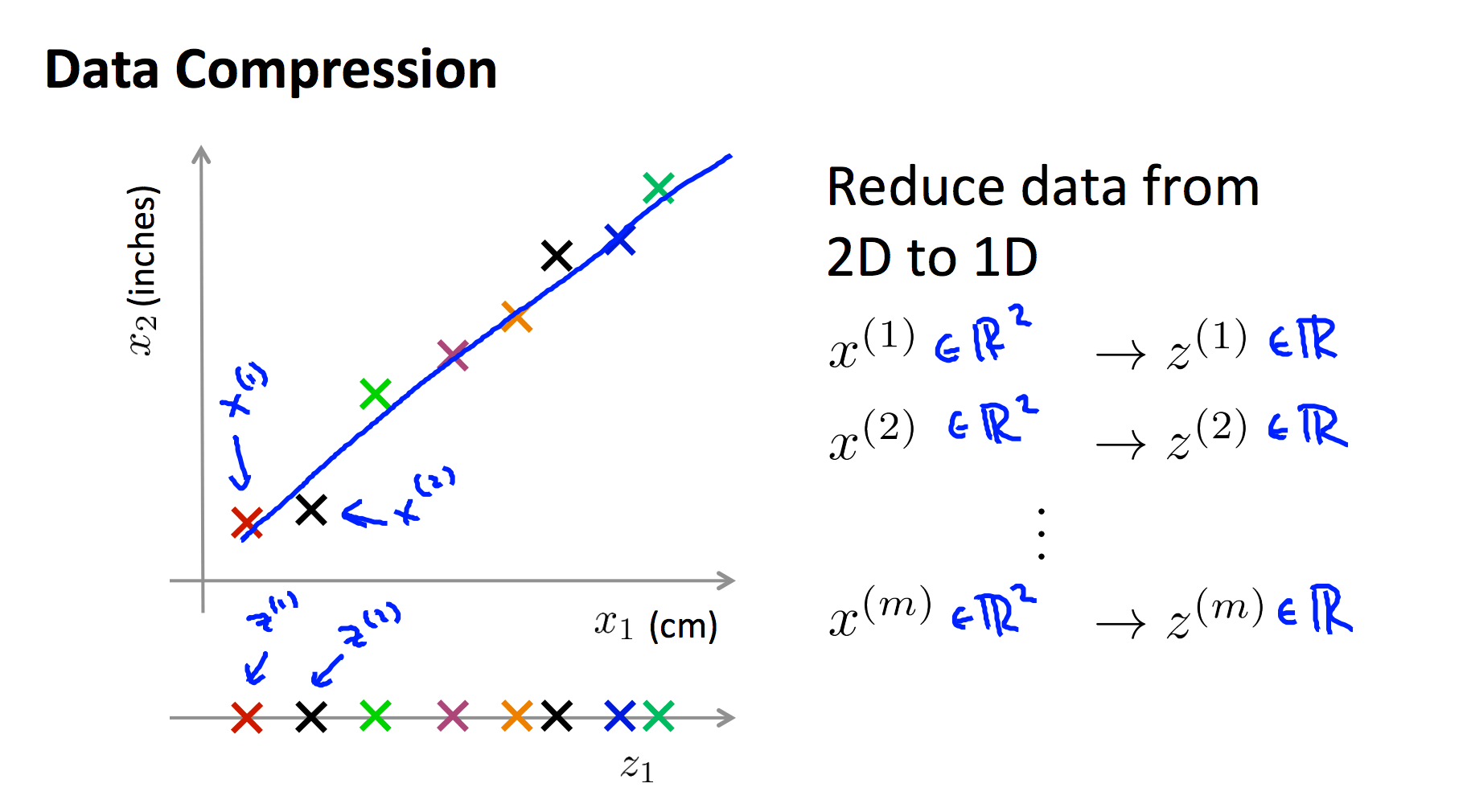
二、主成分分析(PCA)详解
2.1 PCA的基本概念
PCA(Principal Component Analysis)是最常用的降维方法之一,它通过线性变换将原始特征转换为一组线性无关的主成分,这些主成分能够最大程度地保留数据的方差。
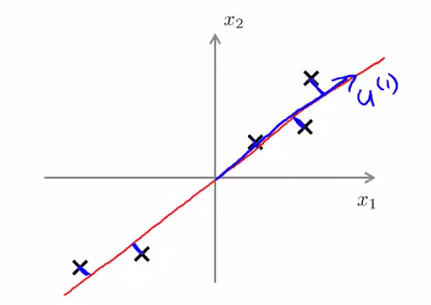
2.2 PCA与线性回归的区别
虽然PCA和线性回归都涉及投影操作,但两者有本质区别:
- 线性回归:最小化预测值与实际值的垂直距离(垂直于y轴)
- PCA:最小化数据点到投影方向的垂直距离
2.3 PCA算法实现步骤
-
数据标准化: $$x^{(i)}_j=\frac{x^{(i)}_j-\mu_j}{s_j}$$ 其中μⱼ是特征j的均值,sⱼ是特征j的标准差
-
计算协方差矩阵: $$\Sigma =\frac{1}{m}\sum_{i=1}^{m}(x^{(i)})(x^{(i)})^T=\frac{1}{m} \cdot X^TX$$
-
奇异值分解(SVD): $$(U,S,V^T)=SVD(\Sigma)$$
-
选择主成分: 取前k个左奇异向量构成降维矩阵U_reduce
-
特征转换: $$z^{(i)}=U^{T}_{reduce} \cdot x^{(i)}$$
2.4 特征还原
由于PCA是有损压缩,我们可以将降维后的特征近似还原: $$x_{approx}=U_{reduce}z$$
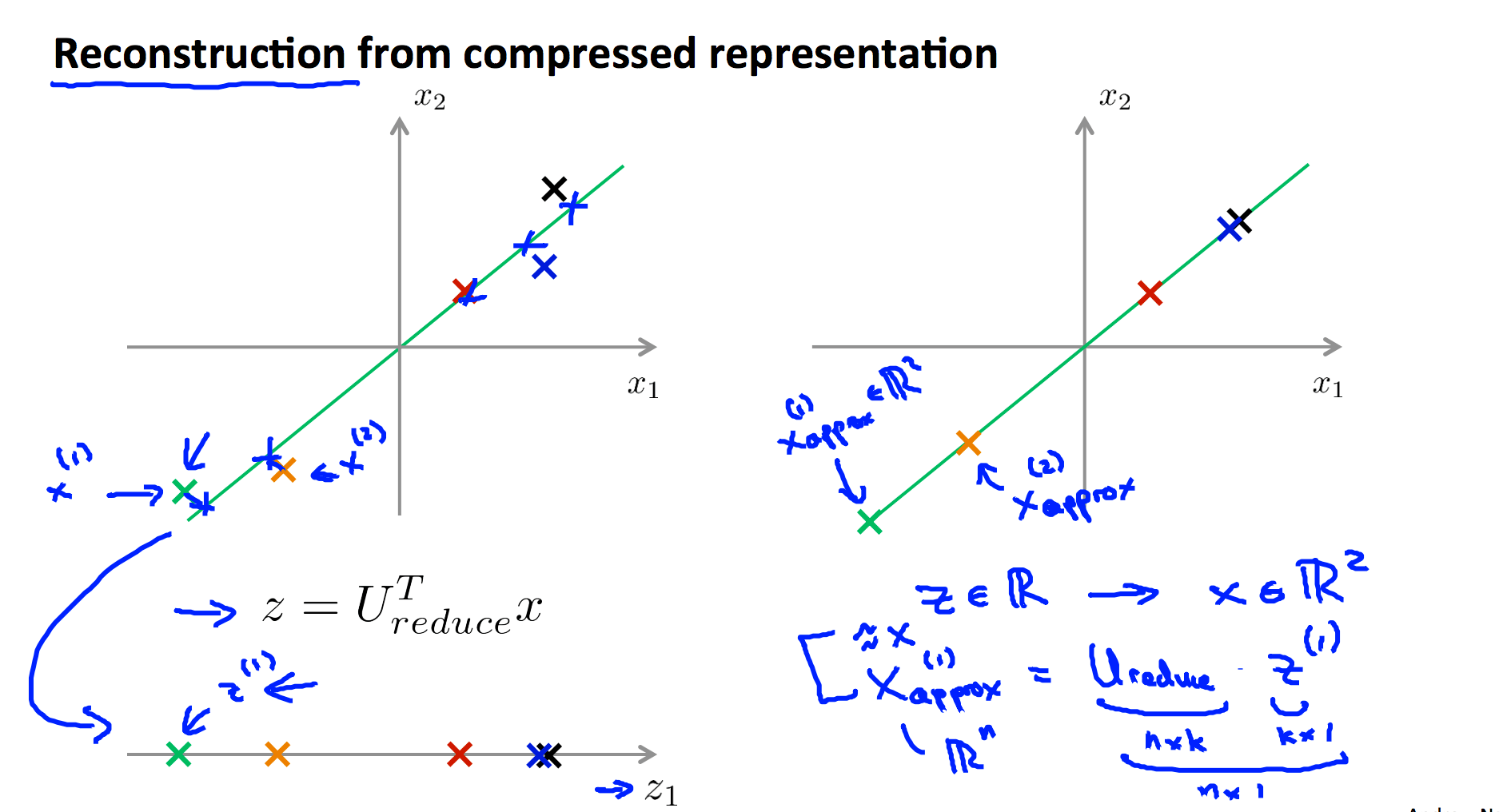
2.5 如何选择降维后的维度k
选择合适的k值对PCA效果至关重要,常用方法是保留一定比例的方差:
-
计算投影均方误差: $$\min \frac{1}{m}\sum_{j=1}^{m}\left | x^{(i)}-x^{(i)}_{approx} \right |^2$$
-
计算数据总变差: $$\frac{1}{m}\sum_{j=1}^{m}\left | x^{(i)} \right |^2$$
-
选择最小的k使得: $$\frac{\min \frac{1}{m}\sum_{j=1}^{m}\left | x^{(i)}-x^{(i)}{approx} \right |^2}{\frac{1}{m}\sum{j=1}^{m}\left | x^{(i)} \right |^2} \leqslant \epsilon$$
通常ε取0.01或0.05,表示保留99%或95%的方差。
三、PCA应用注意事项
3.1 不要过早优化
PCA虽然能降低特征维度,但也可能导致过拟合。在实际应用中,应遵循以下原则:
- 首先尝试不使用PCA的原始模型
- 只有当模型训练速度过慢或内存占用过高时,才考虑使用PCA
- 避免使用PCA来防止过拟合,正则化通常是更好的选择
3.2 PCA的适用场景
PCA最适合用于以下场景:
- 数据压缩:减少存储空间和内存使用
- 数据可视化:将高维数据降至2D或3D以便可视化
- 加速学习算法:当特征维度极高导致算法运行缓慢时
四、PCA测试题解析
4.1 第一主成分方向选择
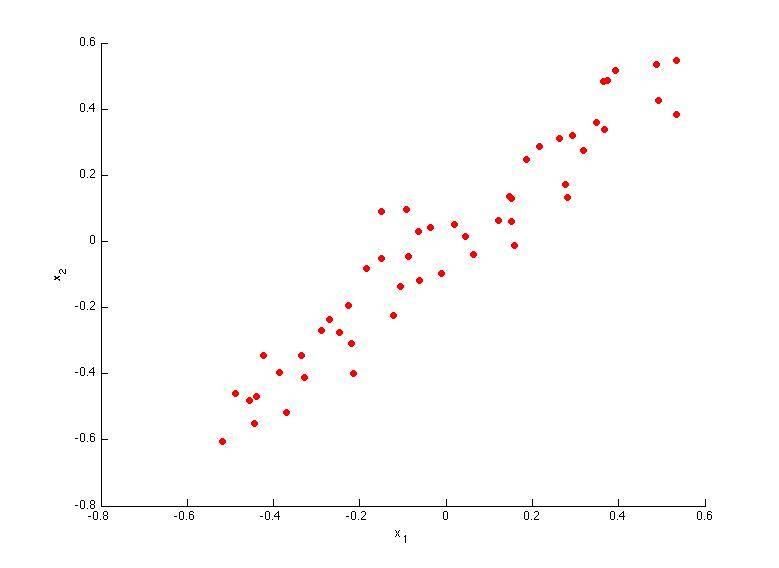
正确答案是A和B,因为第一主成分方向应沿着数据方差最大的方向。
4.2 其他测试题要点
- 选择k值应以保证保留足够方差为前提(如99%)
- "保留95%方差"等价于近似误差不超过5%
- PCA前进行特征缩放非常重要
- PCA主要用于数据压缩和可视化,而非增加特征
五、总结
PCA是一种强大的降维工具,能够有效处理高维数据问题。通过本文的介绍,读者应该掌握了:
- PCA的基本原理和数学实现
- 如何选择合适的降维维度
- PCA的实际应用场景和注意事项
- 常见问题的解决方法
记住,PCA不是万能的,在实际应用中需要根据具体情况谨慎使用。当算法性能良好时,不必刻意使用PCA;只有当面临高维数据带来的具体问题时,PCA才应被考虑作为解决方案之一。
创作声明:本文部分内容由AI辅助生成(AIGC),仅供参考




 项目地址: https://gitcode.com/gh_mirrors/ha/Halfrost-Field
项目地址: https://gitcode.com/gh_mirrors/ha/Halfrost-Field 



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










