基于子地图拼接的平面SLAM算法

一种以平面为特征的基于子地图拼接的 RGB‐D SLAM算法

摘要

本文提出了一种用于在室内环境中重建3D表面的新型RGB‐D SLAM算法。该方法是一种基于子地图拼接、以平面为特征的RGB‐D SLAM算法，因此称为SJBPF‐SLAM。通过两个相邻关键帧及其对应的小块区域和从关键帧中观测到的平面来构建子地图。然后将当前子地图依次融合到全局地图中，同时通过平面特征关联逐步恢复全局结构。使用子地图显著降低了优化过程中的计算成本，同时不丢失任何关于平面和结构的信息。所提出的方法在公开可用的RGB‐D基准数据集上进行了验证，获得了高质量的轨迹和3D模型，而这对现有的RGB‐D SLAM算法而言较为困难。

1 引言

室内环境是机器人应用中最常见的场景之一，实时构建未知环境的高质量地图对于SLAM来说仍是一项具有挑战性的任务。基于点的SLAM算法[1, 2]在各种环境中取得了很大成功，但仍无法处理具有大面积无纹理平面的环境，例如墙壁、地板和天花板。这些区域实际上提供了有用的结构特征，然而在基于点的SLAM中它们被视为挑战。在基于平面的 SLAM中，平面有助于提高机器人位姿和表面估计的精度。高质量稠密地图可用于多种应用，如机器人导航、房地产以及虚拟现实的底图。尽管已有多 种算法被开发用于在SLAM中利用平面，并且大多数算法能够生成相对精确的轨迹，但在复杂室内环境中（例如包含天花板、地板和其他墙壁的长走廊）仍难以获得高质量的模型。

本文提出了一种基于子地图拼接的RGB‐D SLAM算法以平面为特征（SJBPF‐SLAM），该算法比批量离线3D重建更高效，且比现有的 RGB‐D SLAM算法更准确。我们在多个公开可用的挑战性数据集上将所提方法与最先进的方法进行了比较，结果表明我们的方法在轨迹和表面估计质量方面均有提升。

本文组织如下：相关工作在第2节中讨论。3节描述了所提出的方法。具体包括第3.1节中的局部地图构建和第3.2节中的局部地图拼接。4节展示了实验与结果。5节总结了本文并给出了关于该方法的一些未来工作。

2 相关工作

在机器人学、计算机视觉和计算机图形学领域，多年来一直研究平面在SLAM或 3D重建中的应用。

RGB-D SLAM

Kinect风格深度传感器以一种直接的方式提供环境的3D模型。CPA‐SLAM [3]使用全局平面模型对环境进行建模，从而在直接图像对齐的同时减少漂移。在其全局模型中定义了两种残差，一种是点到点距离，另一种是当点位于平面上时点到全局平面的距离。这类残差可能受到深度图像噪声的影响。Kintinuous [4]和弹性融合 [5]没有显式地使用平面，而是采用帧到模型策略来克服漂移。尽管实现了大规模稠密建图，但由于未直接利用平面结构，这两种方法在恢复全局结构时仍存在漂移，如第4节所示。稠密平面SLAM [6]使用平面作为模型的表示形式，然而平面并未包含在状态向量中，因此在地图构建过程中平面未被优化。 [7]提出了一种基于平面地图的快速地点识别算法。

视觉里程计和单目SLAM

平面被探索用于不同的应用和各种传感器。平面基元被应用于为RGB‐D相机提供鲁棒里程计[8]。最近的研究使用平面来提高单目SLAM的精度。Pop‐up SLAM [9]使用深度卷积网络在图像中检测平面，并证明了这类结构可以改善状态估计和稠密建图，尤其是在无纹理环境中。在[10],提出了一种结构化学习算法，通过透视线索将重建模型拟合到房间的“盒子”结构上。利用平行与正交墙壁来校正相机的里程计[11]。在单目场景中，环境的平面结构难以检测，这些方法只能在受限条件下有限的场景中使用。

离线三维重建

[12]提出了一种由细到粗的全局配准方法。具体而言，平面关联窗口在迭代过程中逐渐增大，并在算法结束时覆盖整个序列，该过程称为分层优化。由于所有代价函数在每一步都需要计算，因此该方法仅适用于离线应用。[13]利用环境中标注物体来引导优化，从而获得更优的全局配准结果。在该方法中，使用一个物体的限展作为约束可以显著减少漂移并改善全局配准效果，但对视频序列进行人工标注物体非常耗时。

子地图拼接算法

近年来，基于子地图的方法引起了研究人员的关注[14–16]。稀疏局部子地图拼接滤波器（SLSJF）[15]提出了一种规范且高效的子地图拼接算法，利用一致的局部子地图构建大规模特征地图。他们探索了稀疏结构，并结合一种新颖的状态向量，应用了协方差子矩阵恢复技术。[16]证明了子地图拼接问题可以被表述为一个线性最小二乘问题，从而可以通过闭式解求解。所有这些方法都使用点作为特征。

本文中，我们以平面为特征构建精确局部子地图[15],，并在子地图拼接过程中利用全局地图中的平面结构。

3 方法

我们的框架包含两个主要阶段。首先，我们从每对相邻关键帧构建局部子地图。其次，所有局部子地图通过地图拼接算法以顺序方式连接起来。如图1所示，我们在连续帧之间应用了粗略的视觉里程计。最耗时的计算，即提取小块区域和检测平面，仅在关键帧上进行，并且可以轻松分配到并行进程中。在一个局部子地图中，小块区域有助于提高位姿估计精度并获得更好的图像对齐效果。局部子地图的输出是结束位姿以及从第一个关键帧观测到的平面，这些信息定义在第一个关键帧的局部坐标系中。在图1的底部部分，不同子地图中的多个平面被关联为全局模型中的一个唯一平面。

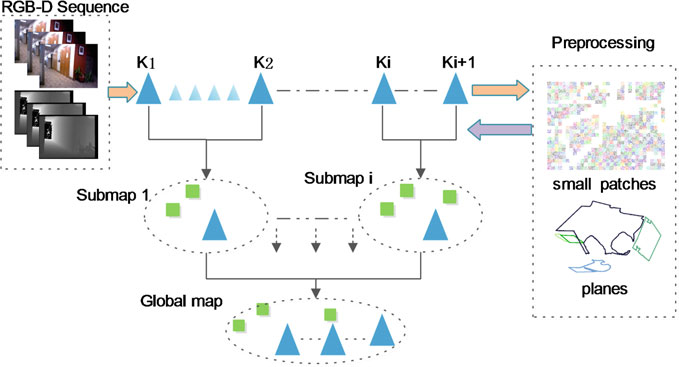
3.1 构建局部子地图

局部子地图基于两个相邻关键帧构建。该阶段的输入为关键帧Ki和Ki+1：包括关键帧Ki观测到的平面系数、两个关键帧上的小块区域以及来自视觉里程计的变换。该阶段的输出是一个局部子地图：信息矩阵、包含关键帧Ki+1位姿的状态向量的最优解，以及从关键帧Ki观测到的平面系数。注意，第一个关键帧Ki的位姿不在状态向量中，因为它定义了子地图的局部坐标系。

3.1.1 预处理

在构建子地图之前，从每个关键帧中提取小块区域和平面。图2a展示了原始的彩色图像和深度图像，图2b显示了提取的小块区域，检测到的平面如图2c所示。

小块提取 。从小块区域从深度图像中检测得到。首先，我们将深度图像均匀划分为n乘n的网格。然后对每个网格单元分别应用RANSAC拟合算法提取平面系数，其中阈值Tpa用于控制内点最小数量。在我们的算法中，一个小块区域表示为 ω={a,b,c,d, pc}，其中{a,b,c,d}是平面的系数，而pc是该面片的锚点。

平面检测 。我们采用两轮聚类方法从深度图像中提取平面。首先，通过利用积分图像高效地计算深度图像中每个像素的法向量[17],，然后根据它们之间的角度进行分类。其次，计算每个点沿法线方向到原点的距离，并利用这些距离对所有像素进行聚类。在两轮聚类结果中位于同一区域的点被认为位于同一平面上。最后，可通过拟合平面上的点来估计平面系数的初始值。

3.1.2 局部相对位姿

在本部分中，我们利用了视觉里程计在局部范围内是准确的这一事实，尽管它在长序列中会存在漂移。幸运的是，我们的子地图正是局部定义的，因此局部子地图中的位姿应接近视觉里程计。我们将视觉里程计作为信息引入，并定义如下误差项：
$$
EL= \sum_{m=1}^{pmax} | Rˆpm+ tˆ − Rpm − t|^2
$$
其中旋转矩阵ˆR和平移向量ˆt来自视觉里程计的测量值，R和t为状态向量中的旋转矩阵和平移向量，点pm是从单位半径球面上均匀选取的常数，pmax是所选点的数量。通过这种方式，我们可以避免对位姿中的角度进行直接测量，并使所有误差均位于欧氏距离[12, 18]下。在本研究中视觉里程计通过在相邻帧上对像素和三维特征位置的残差进行光束法平差来提供，但任何其他合适的视觉里程计算法也应适用于此任务。

3.1.3 基于小块区域的ICP式配准

这种类ICP配准的基本思想是仅使用小块区域进行三维配准，同时以粗略的视觉里程计提供初始值。此类配准利用从小块区域深度值拟合得到的小块系数，而不是从深度图像转换而来的点云，后者通常会受到传感器自身噪声的严重影响。

小块区域关联 。在关键帧Ki+1上观测到的面片通过当前估计位姿变换到关键帧Ki中（首次迭代时使用视觉里程计作为初始猜测）。然后可以在同一坐标系下根据法向量夹角和距离寻找最近的面片。为了更清晰地说明，假设ωi i+1是来自关键帧Ki+1的一个小块区域，并已变换至关键帧Ki的局部坐标系中， ωi是来自关键帧Ki的另一个小块区域。我们通过两个判断准则来确定这两个面片是否构成对应关系：一是两个法向量之间的夹角，二是两个面片之间的距离。为了加快查找对应关系的速度，利用每个面片的中心点构建KD树。这样可以快速找出若干对最近的小块区域，并仅在这些小范围内比较法向量，而无需穷举计算所有距离。关键帧Ki定义了局部坐标系，且其位姿在迭代过程中保持不变，因此我们在该关键帧的面片上建立KD树。来自关键帧Ki+1的面片可用于在KD树中进行查询。这样一来，尽管关键帧Ki+1的位姿会被调整，KD树在整个优化过程中只需创建一次。

代价函数 。我们定义了一个误差项，以最小化两个对应面片之间的距离，旨在获得共面小块区域。
$$
ES= \sum_{k=1}^{kmax} |(Rpc(i+1)(k)+ t)^T · ni + di|^2 + \sum_{k=1}^{kmax} |(R^{-1} (pci(k) − t))^T · ni+1+ di+1|^2
$$
其中旋转矩阵R和平移向量t来自估计的状态向量，{ni, di} ={ai, bi, ci, di}是关键帧Ki上图块的系数，{ni+1, di+1}是关键帧Ki+1上图块的系数，pc(i+1)(k)是关键帧Ki+1上观测到的图块的第k个锚点，pci(k)是关键帧Ki上图块的第k个锚点。在图块的中心点周围选取kmax个锚点。简而言之，该项度量的是左片面片的点与右片面片对应的平面之间的对应关系，反之亦然。在迭代过程中，左右帧之间面片的对应关系将根据右帧估计的位姿进行更新。理想情况下，中心点应恰好位于对应的平面上，可表示为方程 ax+ by+ cz+ d = 0，其中{a,b,c} 是一个面片的单位法向量，d 是该面片到原点的距离， {x, y,z} 是一个锚点的位置。注意，在此代价函数中，相对位姿是唯一的变量，而两帧上各面片的系数被视为常量。

3.1.4 平面对小面片

在本节中，我们描述了平面与小块区域之间的关系。对于由关键帧Ki和Ki+1构建的局部子地图，仅包含从关键帧Ki观测到的平面（仅从关键帧Ki+1观测到的平面将被纳入下一个子地图中，其中Ki+1为起始位姿）。这些平面系数在子地图构建和子地图拼接阶段均被优化。

平面对小面片的关联 。平面与子地图的第一个关键帧上的小块区域相关联，即关键帧 Ki。由于它们定义在同一个坐标系下，因此无需进行坐标变换即可比较它们的法向量和距离。类似于小块区域的关联方法，我们计算两个法向量之间的夹角以及平面与小块区域之间的距离。当夹角和距离均低于某个阈值时，该平面便与该小块区域相关联。通过这种方式，可以找到平面上的所有小块区域。

代价函数 。我们定义了另一个误差项来衡量平面与小块区域之间的关系。通过最小化以下几何误差，旨在获得平面系数。
$$
EPS= \sum_{m=1}^{mmax} \sum_{k=1}^{kmax} |p_c(k)^T · nm+ dm|^2
$$
其中pc(k)是来自小块区域的第k个锚点，nm={am,bm,cm}和dm是平面Ωm的系数，mmax是平面的数量。

由于平面参数化不是最小表示，我们定义了一个误差项来约束平面的法向量，以使表示唯一。
$$
EC= \sum_{m=1}^{mmax} |a_m^2+ b_m^2+ c_m^2 −1|^2
$$

3.1.5 子地图的优化与输出

局部子地图的目标函数定义如下：
$$
ELM= WL EL+ WSES+ WPSEPS+ WCEC
$$
其中，EL、ES、EPS、EC 是前文定义的代价函数，WL、WS、WPS、WC 是各项目对应权重。该函数使用列文伯格‐马夸尔特 (LM) 方法进行优化。子地图的输出是状态向量和信息矩阵的最优解，如(ˆX L, IL)所定义，其中ˆX L （上标“L”表示局部子地图）是状态向量X L=(X L c, X L 1, X L 2, …, X L n)的估计值，IL是相应信息矩阵，通过最后一次迭代中的估计变量计算得到。状态向量包含相机最终位姿X L c（下标“c”表示相机）和平面系数X L 1, …, X L n。由于每个子地图仅包含一个位姿和若干平面系数，优化的收敛速度非常快且稳定。

3.2 局部子地图拼接

该阶段的输入是上一节中构建的局部子地图。局部子地图拼接算法以顺序方式合并所有局部子地图。输出为全局地图，包含所有位姿、平面的系数以及相应的信息矩阵。该算法与SLSJF[15]的主要区别在于，我们通过将局部子地图中的平面与全局结构相关联来探索全局结构，从而以平面为特征而非点为特征。

3.2.1 全局地图中的状态向量

全局地图从第一个局部子地图开始，随着局部子地图的融合而扩展。在1到j−1个局部子地图融合后，全局地图可表示为$(\hat{X} {G}^{j-1}, I {G}^{j-1})$，其中$\hat{X} {G}^{j-1}$是状态向量$X {G}^{j-1}$的估计值，$I_{G}^{j-1}$是相应的信息矩阵，上标“G”表示全局地图。下式给出了状态向量$X_{G}^{j-1}$的详细内容：
$$
X_{G}^{j-1} = (X_{c1}^G, X_{c2}^G, …, X_{c(j-1)}^G, X_{p1}^G, X_{p2}^G, …, X_{pm}^G)
$$
其中$X_c^G$为机器人位姿，$X_p^G$为平面系数。当将局部子地图融合到全局地图时，结束位姿和局部子地图中的新平面被添加作为新变量加入全局地图，与全局地图中已有平面相关联的平面也将被纳入。在融合阶段结束时，全局地图将包含所有的平面和位姿。

3.2.2 融合为一个最小二乘问题

我们将局部子地图与全局地图的融合表述为一个最小二乘问题，该问题将两部分测量值作为输入：前一步得到的全局地图和当前待融合的局部子地图。对于局部子地图$(\hat{X} L^j, I_L^j)$，我们认为结束位姿和平面系数的估计在局部是准确的，可视为真实值的测量，其带有高斯噪声。协方差矩阵可通过信息矩阵给出（信息矩阵的逆即为协方差矩阵）。
$$
\hat{X}_L^j = H_j(X_G^j) + w_j
$$
其中$H_j$是一个变换函数，利用局部子地图的起始位姿（即全局地图的最后一位姿）将变量从全局坐标系转换到当前局部坐标系，$w_j$是零均值高斯“观测噪声”，其协方差矩阵为
$$
P_L^j = (I_L^j)^{-1}
$$
类似地，全局地图$(\hat{X}_G^{j-1}, I_G^{j-1})$也可被视为位姿和平面系数真实值的测量值，带有高斯噪声。协方差矩阵也可以由信息矩阵给出。即
$$
\hat{X}_G^{j-1} = X_G^{j-1} + W {j-1}
$$
其中$W_{j-1}$是均值为零的高斯“观测噪声”，其协方差矩阵为$P_G^{j-1} = (I_G^{j-1})^{-1}$。

由上文可知，第$j$个局部子地图与第$(j - 1)$个全局地图的融合可以表述为一个最小二乘问题，利用来自全局地图和局部子地图的所有信息。以下方程展示了该加权最小二乘问题：
$$
\min_{X_G^j} (\hat{X}_L^j - H_j(X_G^j))^T I_L^j (\hat{X}_L^j - H_j(X_G^j)) + (\hat{X}_G^{j-1} - A_j X_G^j)^T I_G^{j-1}(\hat{X}_G^{j-1} - A_j X_G^j)
$$
其中$A_j$是一个从已存在于$\hat{X}_G^j$中的变量中提取对应变量的矩阵。该问题可使用高斯‐牛顿算法求解。

3.2.3 数据关联

算法1中的数据关联用于寻找局部地图与全局地图之间的平面对应关系。设$\Omega_G$为全局地图中的平面特征，$P_G$为其对应的协方差矩阵。设$\Omega_L$为局部子地图中的平面特征，$P_L$为其对应的协方差矩阵。全局地图中的平面特征$\Omega_G$通过变换被转换到当前局部子地图的局部坐标系$\bar{\Omega} G$中：
$$
\bar{\Omega}_G = H(\Omega_G), \quad H(\Omega_G) = ((R_e)^{-1}n_G, t_e^T n_G + d_G)
$$
其中$\Omega_G = {n_G, d_G}$，$p_e^G = {R_e, t_e}$。$H(\Omega_G)$利用相机在全局地图中的结束位姿$p_e^G$（“e”表示全局地图中的结束位姿），将平面系数$\Omega_G$从全局坐标系转换到局部坐标系。然后我们定义一个马氏距离：
$$
d {gl} = (\bar{\Omega} G - \Omega_L)^T(\bar{P}_G + P_L)^{-1}(\bar{\Omega}_G - \Omega_L)
$$
其中$\bar{P}_G$是变换后全局地图的协方差矩阵。因此，可以根据$\chi^2$分布选择适当的阈值$d {min}$，使得在某一置信水平下，原假设“两个特征为同一特征”不被拒绝。该过程在每次迭代中重复执行。

4 实验与评估

在本节中，我们对SJBPF‐SLAM算法进行了评估，并将其与最先进的方法进行比较。评估中使用了三个公开可用的数据集：ICL‐NUIM合成场景[19]和普林斯顿大学SUN3D数据集[13]和TUM数据集[20]。ICL‐NUIM合成场景具有真实值，而SUN3D数据集提供了具有明显几何结构的挑战性场景，可用于比较重建表面。

局部子地图的构建本质上是并行的，因此可以分配到不同的计算单元上。对于子地图拼接算法，尽管状态向量随着局部子地图的拼接而线性增长，但在常见场景中平面特征的数量是有限的。目前，整个SLAM算法在MATLAB中实现，并在Intel Core i5‐6300、2.30GHz、8G RAM的环境下进行评估。在计算时间方面，每帧预处理耗时约2秒，构建一个子地图约需4秒。子地图拼接能够实时运行。

我们设置$p_{max}= 8$，$k_{max}= 6$用于球面和平面上的采样点选择。关键帧通过测量运动或当帧数达到$m= 5$时进行选取。局部子地图构建阶段的权重设置为：$W_{PS}= 1, W_L= 2, W_S=1, W_C= 10$。阈值$T_{pa}$在我们的数据集中设置为0.95。LM算法在每个子地图中经过3–4次迭代后收敛。而在子地图拼接阶段，我们无需手动设置权重，信息矩阵提供了不确定性信息，并作为优化中的权重使用。采用高斯‐牛顿的地图拼接算法仅需2次迭代即可快速收敛。

4.1 轨迹估计

在第一次实验中，我们通过使用存在噪声的ICL‐NUIM合成场景并将结果与真实值进行比较，评估了SJBPF‐SLAM的性能。将来自全局地图的轨迹与真实值轨迹进行对比。表1展示了与绝对轨迹误差（ATE）的对比结果。我们将SJBPF‐SLAM算法与其他先进的RGB‐D SLAM系统进行了比较，包括弹性融合 [5], Kintinuous[4], RGB-D SLAM[2], MRSMap[21], DVO-SLAM[22], 以及一些基于平面的方法：CPA‐SLAM [3]和稠密平面SLAM [6]。表1 显示了与这些方法的对比结果。许多系统在某些数据集上的表现不佳，例如，DVO‐SLAM的最大误差为0.191（在数据集kt2上），RGB‐D SLAM为0.433（在数据集kt3上），MRSMap为1.090（在数据集kt3上），Kintinuous为0.355（在数据集kt3上），弹性融合为0.106（在数据集kt3上），稠密平面SLAM为0.246（在数据集kt1上），CPA‐SLAM的表现与我们的方法相似，但其计算依赖于GPU。由于我们的SJBPF‐SLAM探索了全局结构并从中受益，其最大误差低于之前大多数SLAM系统。

4.2 表面估计

为了评估我们方法的表面估计性能，我们将全局地图与其他最先进的方法的输出进行了比较。如图3a所示，在未使用任何平面信息的批量捆绑调整（BA）输出中，两堵墙壁之间存在间隙。我们对我们的SJBPF‐SLAM进行了评估。

同一数据集[19], 从图3b中可以看出，全局结构得到了很好的重建。图3c、d展示了两个模型的更多细节，标明了我们方法的显著改进。我们还在TUM数据集上测试了我们的方法[20], 如图4所示。模型显示了被高亮的平面。地板上的大平面以及其他一些人工物体，例如棋盘格、桌子，在我们的平面模型中被检测并保持。图5a显示了Kintinuous [4]在SUN3D [13], 数据集上的结果，该数据集是在一条长走廊中采集的。Kintinuous在此具有挑战性的场景中失败，原因是跟踪错误。弹性融合 [5]在数据集的大部分区域表现良好，但在走廊末端附近也出现了漂移，如图5b所示。图5c显示了我们的SJBPF‐SLAM方法的输出。通过子地图拼接在算法中维持全局结构，有助于精确重建环境的3D模型。

5 结论与未来工作

本文提出了一种SJBPF‐SLAM算法，该算法利用人造室内场景中的平面，可用于构建高质量的3D模型。该算法应用了子地图拼接技术，因此非常高效。全局结构通过拼接新的子地图逐步恢复，这些子地图基于局部帧构建，因而非常精确。实验表明，我们的算法生成的3D模型优于大多数最先进的 RGB‐D SLAM算法，且我们的算法比离线三维重建更高效。

未来，我们将改进该算法，使其能够鲁棒地处理大回环和一些动态物体。我们还将把研究扩展到包含非平面区域和人造场景中常见物体（如椅子和桌子）的环境。在动态环境中实现鲁棒的RGB‐D SLAM的主动感知也是我们未来的研究方向。