本文详细解析了二叉树的基本概念，包括高度、深度和层的定义，探讨了二叉树的存储方式及遍历算法，并深入讲解了二叉查找树的查找、插入、删除操作及其复杂度分析。
树
关于树，有几个比较相似的概念：高度(Height)、深度(Depth)、层(Level)
定义：
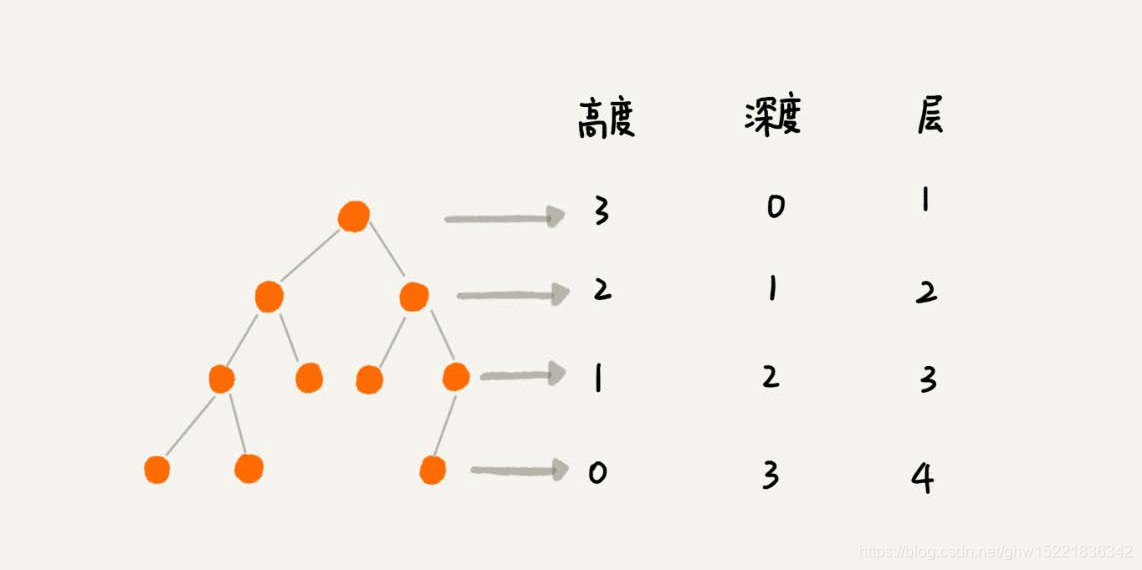
- 节点高度=节点到叶子节点的最长路径；
- 节点深度=根节点到这个节点所经历的边的个数；
- 节点层数=节点深度+1；
- 树的高度=根节点的高度；
二叉树(binary tree)
二叉树，每个节点有两个叉，分别是左子节点和右子节点；
满二叉树，就是除了叶子节点之外，其余的所有节点都有左右两个子节点；
完全二叉树，为什么最后一层的叶子节点靠左排列的叫完全二叉树呢？为啥靠右排列的就不能叫完全二叉树呢？
思考一下如何来存储二叉树呢？
1、基于指针或者引用的二叉链式存储法
简单、直观的链式存储法，每个节点有三个字段，其中一个存储数据，另外两个是指向左右子节点的指针，只要抓住根节点，就可以通过左右子节点的指针，把整棵树都串联起来，如下图所示：
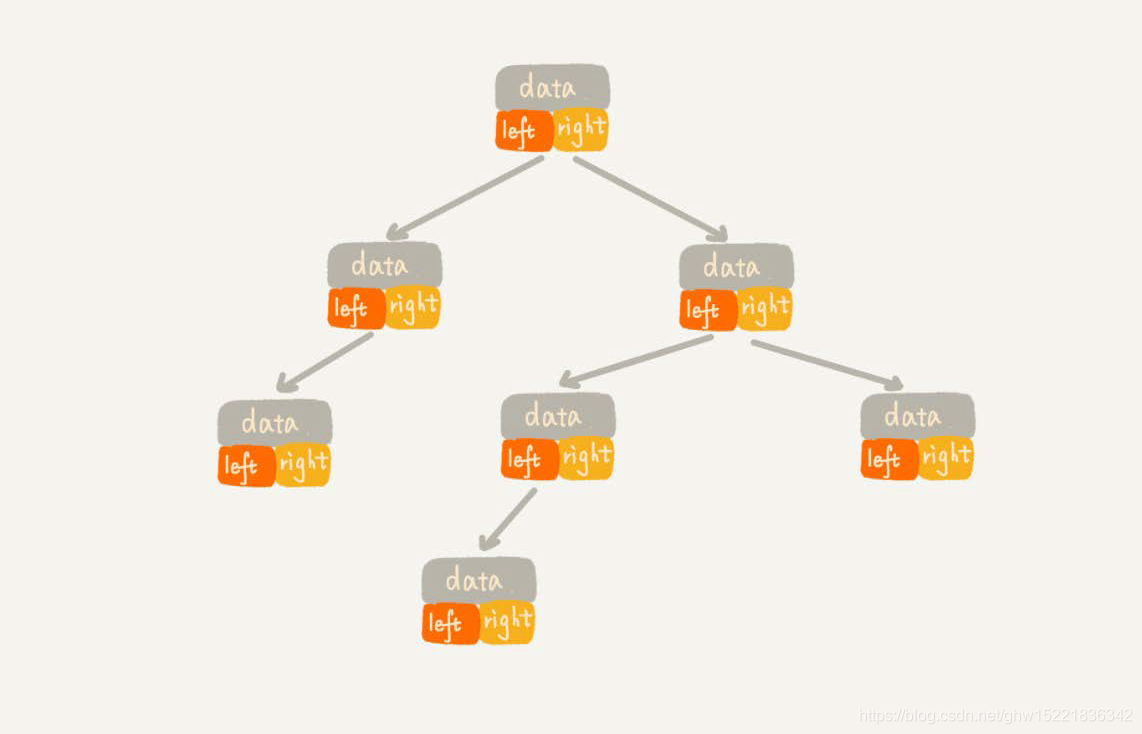
2、基于数组的顺序存储法
根节点存储在下标i=1的位置，那么左子节点存储在下标2i=2的位置，右子节点存储在2i+1=3的位置，依次类推：B节点的左子节点存储在2i= 22 =4的位置，右子节点存储在2*i+1=5的位置；
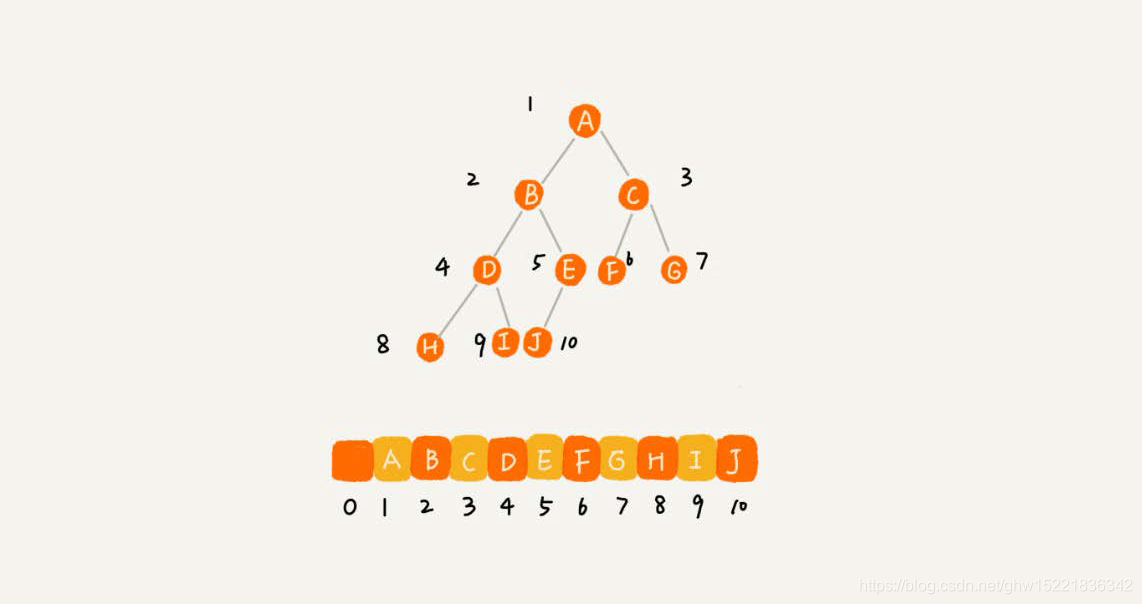
总结:节点X存储在数组中下标为i的位置，下标为2i的位置存储的就是左子节点，下标为2i+1存储的就是右子节点；
所以如果某棵树是完全二叉树，采用顺序数组存储的方式无疑是最省内存的，因为不需要额外的存储空间来存储左右子节点的指针；所以完全二树最后一层的叶子节点都要靠左排列，是因为不想造成额外的内存资源浪费；
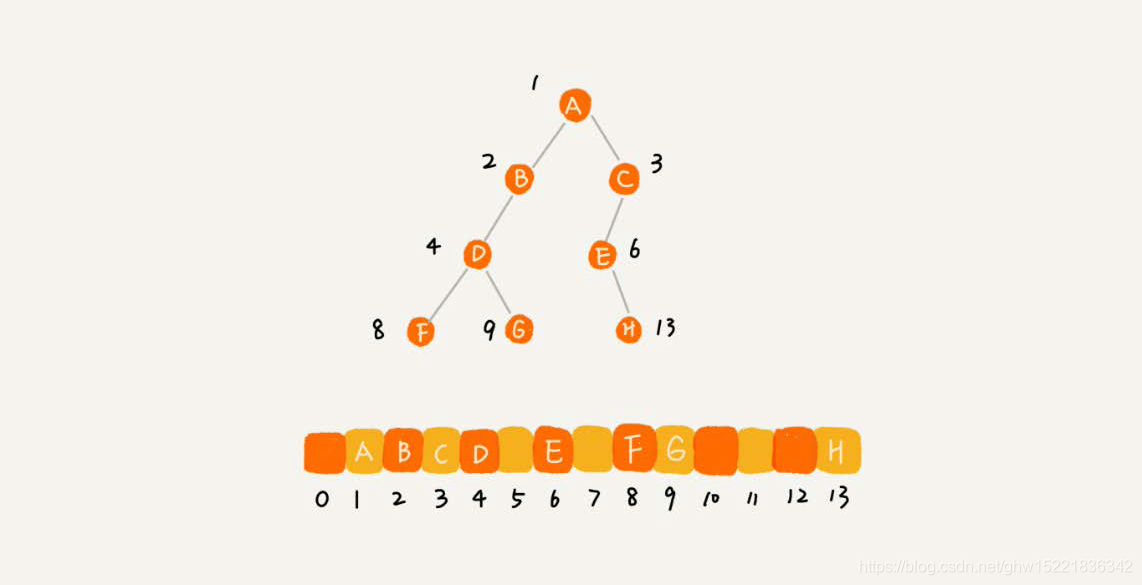
二叉树的遍历
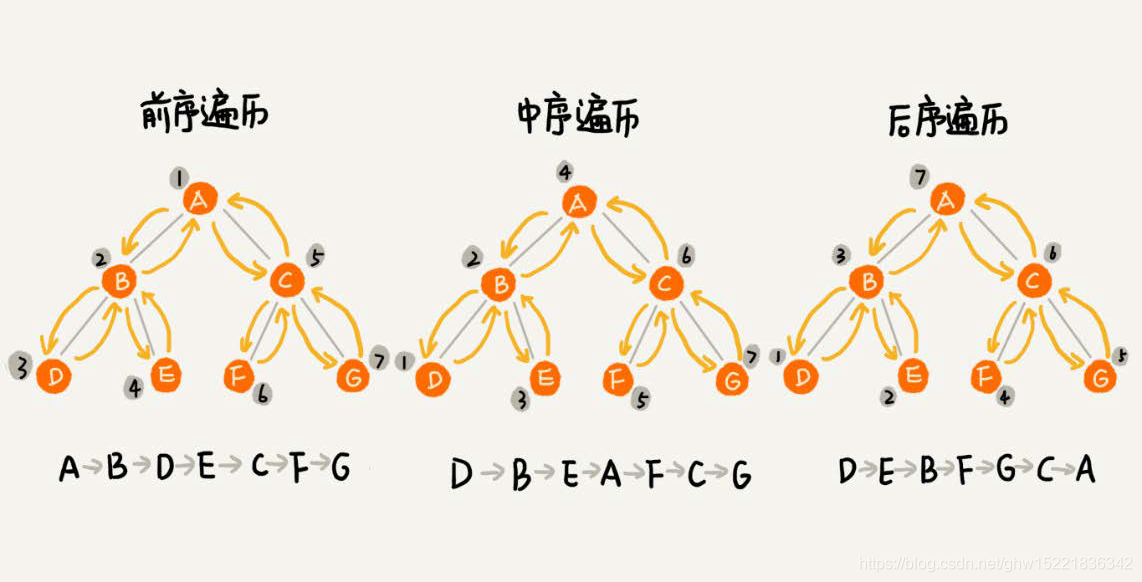
- 前序遍历，对于树中的任意节点，先打印节点，然后在打印左子节点，最后打印它的右子节点；
- 中序遍历，对于树中的任意节点，先打印它的左子树，然后在打印它本身，最后打印出它的右子节点；
- 后序遍历，对于树中的任意节点，先打印它的左子树，然后在打印它的右子树，最后打印出这个节点本身；
代码实现
前、中、后序遍历就是一个递归的过程，递推公式如下：
前序遍历的递推公式
preOrder = print(root)->print(root.left)->print(root.right)
中序遍历的递推公式
inOrder = print(root.left)->print(root)->print(root.right)
后序遍历的递推公式
postOrder = print(root.left)->print->(root.right)->print(root)
class TreeNode{
int value ;
TreeNode right;
TreeNode left;
TreeNode(int value){
this.value = value;
}
}
//递归实现
//前序遍历
public static void preOrder(TreeNode root){
if(root==null) return;
System.out.println(root.value);
TreeNode leftTree = root.left;
if(leftTree!=null)
{
preOrder(leftTree);
}
TreeNode rightTree = root.right;
if(rightTree!=null)
{
preOrder(rightTree);
}
}
//非递归实现
public static void preOrder(TreeNode root){
Stack<TreeNode> stack = new Stack<TreeNode>();
while(root!=null||!stack.isEmpty()){
if(root!=null)
{
//先打印根节点，然后在打印左子节点，并且将其依次压入栈中
System.out.println(root.value);
stack.push(root);
root = root.left;
}else{
//当最后的左子节点没有子树时，在依次从栈中弹出节点，并且打印右子节点
root = stack.pop();
root = root.right;
}
}
}
//中序遍历
//递归实现
public static void inOrder(TreeNode root){
if(root == null) return;
TreeNode leftTree = root.left;
if(leftTree != null)
{
inOrder(leftTree);
}
System.out.println(root.value);
TreeNode rightTree = root.right;
if(rightTree != Tree)
{
inOrder(rightTree);
}
}
//非递归实现
public static void inOrder(TreeNode root){
Stack<TreeNode> stack = new Stack<TreeNode>();
while(root!=null||!stack.isEmpty()){
if(root!=null)
{
stack.push(root);
root = root.left;
}else{
root = stack.pop();
System.out.println(root.value);
root = root.right;
}
}
}
//后序遍历
//递归实现
public static void postOrder(TreeNode root){
if(root ==null)
return;
else{
postOrder(root.left);
postOrder(root.right);
System.out.println(root.value);
}
}
//非递归实现
public static void postOrder(TreeNode root){
int left = 1;//辅助栈中标记为左节点
int right = 2;/辅助栈中标记为右节点
Stack<TreeNode> stack = new Stack<TreeNode>();
Stack<TreeNode> stack2 = new Stack<TreeNode>();//辅助栈
while(root!=null||!stack.isEmpty()){
while(root!=null)
{
//将节点压入栈1，并且在在栈2中将其标记为左节点
stack.push(root);
stack2.push(left);
root = root.left;
}
if(!stack.isEmpty()&&stack2.peek()==left)
{
//如果是从左节点返回父节点，则标记为右节点
stack2.pop();
stack2.push(right);
root = stack.peek().right;
}
while(!stack.isEmpty()&&stack2.peek()==right)
{
//如果是从右子节点返回父节点，则任务完成，将两个栈的栈顶弹出
stack2.pop();
System.out.println(stack.pop().value);
}
}
}
//一个栈实现后序遍历
public void postOrder(TreeNode){
if(root!=null){
Stack<TreeNode> stack = new Stack<TreeNode>();
stac.push(root);
TreeNode cur = null;
while(!stack.isEmpty()){
cur = stack.peek();
if(c.left!= null&&root!=cur.left&&root!=cur.right)
stack.push(cur.left);
else if(cur.right!=null&&root!=cur.right)
stack.push(cur.right);
else{
System.out.println(stack.pop());
root = cur;
}
}
}
System.out.println();
}
对于非递归实现的遍历，建议自己画个树，顺着代码走一遍，这样理解起来会简单一些，千万不要死记硬背代码的实现，因为睡一觉啥都记不起来了！
时间复杂度
二叉树的遍历与节点个数n成正比，所以二叉树遍历的时间复杂度是O(n);
二叉查找树(Binary Search Tree)
二叉查找树的要求，在树中的任意一节点，其左子树的每个节点的值，都小于该节点的值，其右子树节点的值都大于该节点的值；
查找
在二叉查找树中查找一个节点，先取根节点，如果要查找的数据就是根节点，直接返回；如果要查找的数据比根节点的值要小，那就在左子树中递归查找；如果要查找的数据比根节点的值要大，那就在右子树中递归查找；
代码如下：
public class BinarySearchTree{
private Node tree;
public Node find(int data){
Node p = tree;
while(p!=null){
if(data<p.data) p = p.left;
else if(data>p.data) p = p.right;
else{
return p;
}
}
}
public static class Node{
private int data;
private Node left;
private Node right;
public Node(int data){
this.data = data;
}
}
}
插入
从根节点开始依次进行比较：
- 如果要插入的数据比节点的数据大，并且节点的右子树为空，就将新数据直接插入到右子节点的位置；如果不为空，就再递归遍历右子树，查找插入位置；
- 如果要插入的数据比节点的数据小，并且节点的左子树为空，就将新数据直接插入到左子节点的位置；如果不为空，就再递归遍历左子树，查找插入位置；
public void insert(int data){
if(tree==null){
tree = new Node(data);
return;
}
Node p = tree;
while(p!=null){
if(data>p.data){
if(p.right==null)
{
p.right =new Node(data);
return;
}
p = p.right;
}else{
if(p.left==null){
p.left = new Node(data);
return;
}
p = p.left;
}
}
}
删除
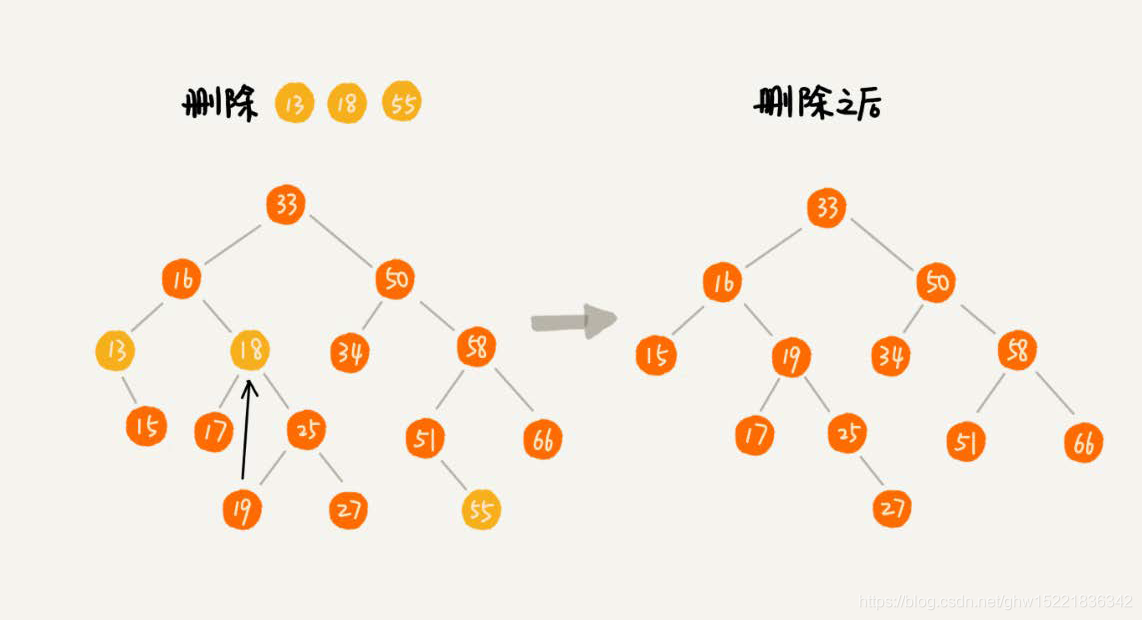
根据要删除的节点个数不同，二叉查找树的删除操作分为三种情况来考虑：
- 删除节点没有子节点，直接将父结点中指向该节点的指针为null;
- 删除的节点只有一个子节点，只需要更新父结点中，指向删除节点的指针，让它指向删除节点的子节点；
- 删除的节点有两个子节点，我们需要找到这个节点的右子树中的最小节点，把它替换到要删除的节点中，因为最小节点肯定没有左子节点；
代码如下：
public void delete(int data){
Node p = tree;//p指向要删除的节点，初始化指向根节点
Node pp = null;//pp记录的是是p的父节点
while(p!=null&&p.data!=data)
{
pp = p;
if(data>p.data) p = p.right;
else p = p.left;
}
if(p==null) return;//没有找到
//要删除的有两个子节点
if(p.left!=null&&p.right!=null){
//查找右子树中的最小节点
Node minP = p.right;
Node minPP = P;//minPP表示minP的父节点
while(minP.left!=null){
minPP = minP;
minP = minP.left;
}
p.data = minP.data;//将minP的数据替换到p中
p = minP;
pp = minPP;
}
//删除节点是叶子节点或者仅有一个子节点
Node child;
if(p.left!=null) child =p.left;
else if(p.right!=null) child = p.right;
else child = null;
if(pp==null) tree = child;
else if(pp.left==p) pp.left = child;
else child = null;
}
public Node findMin() {
if (tree == null) return null;
Node p = tree;
while (p.left != null) {
p = p.left;
}
return p;
}
public Node findMax() {
if (tree == null) return null;
Node p = tree;
while (p.right != null) {
p = p.right;
}
return p;
}
中序遍历二叉查找树，可以输出有序的数据序列，时间复杂度是O(n);
复杂度分析
不管是插入、查找、删除操作，时间复杂度都是和树的高度成正比的，那么如何求一棵包含n个节点的完全二叉树的高度？
对于包含n个节点的完全二叉树中，第一层包含1个节点，第二层包含两个节点，第三层包含4个节点，依次类推，第K层包含的节点个数就是2^(K-1);
那么n满足的关系式如下：
- n>=1+2+4+8+…+2^(L-2)+1
- n<=1+2+4+8+…+2^(L-1);
所以层数的范围是[log2(n+1), log2n +1],也就是说完全二叉树的高度小于等于log2(n);
所以，插入、删除、查找操作的时间复杂度是O(logn);
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
