揭秘LSTM的核心计算原理

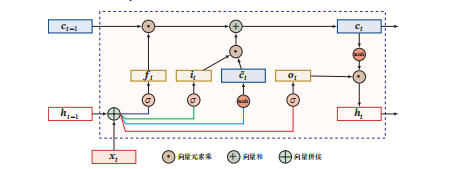
1. 输入门（Input Gate）计算

输入门决定当前时刻网络要向细胞状态中添加多少新信息。

• 首先，将当前时刻输入 xt​ 与上一时刻隐藏状态 ht−1​ 进行向量拼接，然后通过一个带有 Sigmoid 激活函数（σ）的全连接层，得到输入门的输出 it​：it​=σ(Wi​⋅[ht−1​,xt​]+bi​)Sigmoid 函数输出范围在 (0,1)，值越接近 1 表示 “允许大量新信息输入”，越接近 0 表示 “阻止新信息输入”。

2. 候选细胞状态（c~t​）计算

候选细胞状态是当前时刻可能要加入细胞状态的 “新候选信息”。

• 同样将 xt​ 与 ht−1​ 向量拼接后，通过带有 Tanh 激活函数的全连接层，得到候选细胞状态 c~t​：c~t​=tanh(Wc​⋅[ht−1​,xt​]+bc​)Tanh 函数输出范围在 (−1,1)，用于生成 “可被输入门调节的候选内容”。

3. 遗忘门（Forget Gate）计算

遗忘门决定上一时刻细胞状态 ct−1​ 有多少要被 “遗忘”（即保留多少到当前时刻）。

• 把 xt​ 与 ht−1​ 向量拼接后，通过 Sigmoid 激活函数的全连接层，得到遗忘门输出 ft​：ft​=σ(Wf​⋅[ht−1​,xt​]+bf​)Sigmoid 输出的 ft​ 同样在 (0,1) 之间，值越接近 1 表示 “保留越多上一时刻细胞状态”，越接近 0 表示 “遗忘越多”。

4. 细胞状态 ct​ 的更新

当前时刻细胞状态 ct​ 由两部分组成：

• 上一时刻细胞状态经遗忘门 “筛选” 后保留的部分：ft​⊙ct−1​（⊙ 表示向量元素乘）。
• 当前时刻候选细胞状态经输入门 “筛选” 后加入的部分：it​⊙c~t​。两者相加得到新的细胞状态：ct​=ft​⊙ct−1​+it​⊙c~t​

5. 输出门（Output Gate）与隐藏状态 ht​ 计算

输出门决定细胞状态 ct​ 有多少要被输出为当前时刻的隐藏状态 ht​。

• 先计算输出门：将 xt​ 与 ht−1​ 向量拼接后，通过 Sigmoid 激活函数的全连接层，得到输出门 ot​：ot​=σ(Wo​⋅[ht−1​,xt​]+bo​)
• 再对细胞状态 ct​ 做 Tanh 变换（将值压缩到 (−1,1)），然后与输出门 ot​ 做向量元素乘，得到当前时刻隐藏状态 ht​：ht​=ot​⊙tanh(ct​)

通过遗忘门、输入门、输出门的协同作用，LSTM 能灵活控制信息的 “遗忘”“输入” 与 “输出”，从而有效处理长序列的依赖关系。

公式中符号的意义

sigma(\cdot) ：Logistic函数，将输入映射到 [0,1] 区间，用于遗忘门、输入门、输出门的激活，控制信息流通比例。

tanh(\cdot) ：双曲正切函数，将输入映射到 [-1,1] 区间，用于生成候选记忆 \tilde{C_t} ，引入非线性变换。

odot ：向量元素级乘积（Hadamard乘积），实现门控单元与记忆状态的逐元素相乘，按比例控制信息保留/传递。

C_t ：LSTM内部状态（记忆单元），专门传递长程信息，记录序列关键记忆。

 h_t ：隐藏层外部状态，接收并输出经非线性处理的信息，作为后续输入。

C_{t-1} ：上一时刻内部状态（记忆单元），承载历史记忆信息。

tilde{C_t} ：当前时刻候选记忆，由输入与上一时刻外部状态经非线性变换生成，待融入记忆单元。

 f_t ：遗忘门，输出 [0,1] 区间向量，控制上一时刻记忆 C_{t-1} 的遗忘比例。

 i_t ：输入门，输出 [0,1] 区间向量，控制候选记忆 \tilde{C_t} 的融入比例。

 o_t ：输出门，输出 [0,1] 区间向量，控制内部状态 C_t 向外部状态 h_t 的输出比例。

x_t ：当前时刻输入向量，为序列在 t 时刻的输入信息。

W_i, U_i, b_i 等（权重、偏置）：模型可训练参数，对输入 x_t 和上一时刻外部状态 h_{t-1} 做线性变换，是门控与记忆计算的核心参数。