第4章决策树（算法原理+手编实现+库调用）

最新推荐文章于 2022-03-21 10:26:22 发布

原创最新推荐文章于 2022-03-21 10:26:22 发布 · 1.9k 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #决策树 #DecisionTree #编程实现

俯视机器学习专栏收录该内容

9 篇文章

订阅专栏

俯视机器学习

三分天注定，七分靠打代码，爱打才会赢！

第4章决策树

1. 概述

通过多次判断，建立树形结构。

问题：

每次判断中选择什么属性？

基本术语：

纯度

2. 基尼系数、熵、信息增益

基尼值：某事件有 $K$ 种取值，每种取值概率为 $p_i, i=1,...,K$ 。则其基尼值（基尼不纯度）为
$\sum_{i=1}^K p_i (1- p_i) = 1 - \sum_{i=1}^K p_i^2$
基尼值越接近 $0$ ，纯度越高。基尼值可以理解为两次取样的样本不同的概率。
熵：字母含义同上，熵定义为
$-\sum_{i=1}^K p_i \log p_i$
当 $K = 2$ 时，随着 $p_1$ 的变化，基尼系数和熵的变换如下：

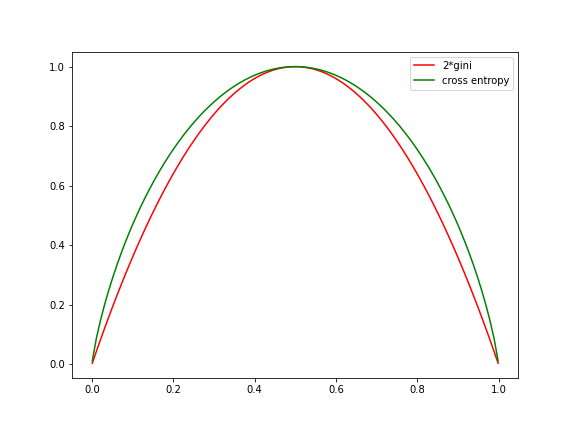
信息增益

当一个数据集被划分成子集后，不确定度应该减少。这里用熵来衡量不确定度。

添加某一属性后，数据集 $D$ 划分后的熵定义为
$\sum_v \frac{|D_v|}{|D|}E(D_v)$
$a$ 为数据的其中一个属性，其中 $v$ 为属性 $a$ 的其中一个取值， $D_v$ 为取值为 $v$ 的样本集。这里的 $E(D_v)$ 和 $E (p)$ 含义类似，下文不再赘述。

信息增益定义为划分前后系统的熵的减少量
$\sum_a E(D|a)$
给定属性后的基尼指数
$\sum_v \frac{|D_v|}{|D|} G(D_v)$
基尼不纯度的减少量为
$\sum_a G(D|a)$

3. 决策树算法

参考周志华《机器学习》。

输入：训练数据集 $D=\{(x_i, y_i\}_{i=1}^m$ ，每个样本 $x_i$ 有 $d$ 个属性，属性几何记为 $A=\{a_i\}_{i=1}^d$ 。

节点表示：每个节点应包含内容

该节点拥有的数据 $D$
该节点拥有的可选属性集 $A$
该节点是父节点属性值的哪个分支（测试时使用） $B$
该节点的子节点集合 children

最优属性选择算法：

给定初始数据 $D$ ，其属性集合为 $A$

对数据 $D$ ，计算初始熵（或基尼值） $E_0$
遍历所有属性，对 $A$ 每一个属性 $a$ ：
- 计算按属性 $a$ 划分后的熵 $E_a$
- 计算熵增益 $Gain = E_0 - E_a$ ，如果熵增最大，记录当前属性
根据最大熵增获得最佳属性 $a^*$

决策树建树过程：函数 TreeGenerate(D, A, B='')

生成节点 $n o d e (D, A, B)$ ，分支 $B$ 默认为空
if $D$ 中样本全部属于同一类别 $C$ :
- 将 $n o d e$ 标记为 $C$ 类叶节点; return node
if $A=\Phi$ or $D$ 中样本在 $A$ 上取值相同：
- 将 $n o d e$ 标记为叶节点，其类别标记为 $D$ 中样本最多的类; return node
从 $A$ 中选取最优划分属性 $a^*$
for $a^*$ 的每一个值 $a_v^*$ ：
- 令 $D_v$ 表示 $D$ 在 $a^*$ 上取值为 $a_v^*$ 的样本子集， $\ { a ∗ } A'=A\backslash \{a^* \}$ ， $B'= a_v^*$ 。
- if $D_v$ 为空：
  - 为 $n o d e$ 生成一个子节点 $subnode(D_v, A', B')$ ；
  - 将子节点 $s u b n o d e$ 标记为叶节点。其类别标记为 $D$ 中样本最多的类，并添加进 $n o d e$ 的 children。 return node
- else:
  - 以 subnode = TreeGenerate( $D_v, A', B'$ )
  - 把 $s u b n o d e$ 加入 $n o d e$ 的 children
return node

输出：以 $n o d e$ 为根节点的一棵决策树。

4. 常见术语

分类。分类决策树中，直接以叶子节点类别作为最终类别。
回归。回归决策树中，将叶子节点的值（如果叶子节点有多个样本，则取这些样本均值）作为回归的值。
过拟合
欠拟合

5. 剪枝

决策树有很强的数据拟合能力，通常情况下，如果不加以限制，决策树能在训练集上拟合所有数据，即训练集上准确率为 $100$ ，容易导致过拟合。剪枝可以有效减轻过拟合。具体而言，剪枝又分为预剪枝和后剪枝。两种剪枝中，先预留一部分数据用作验证集。

预剪枝：在建立决策树过程中，如果对决策树进行进一步分支时，在验证集中表现变差，则终止决策树分支。
后剪枝：先建立完整的决策树，然后有底向上，如果把叶节点和上一级的节点合并后，在验证集中表现编号，则合并节点。

6. 实战：决策树编程实现

import numpy as npimport numpy as np
import pandas as pd
import string
import matplotlib.pyplot as plt
from collections import Counter


class Node:
    def __init__(self, X, y, A, B=None):
        self.optimalAttr = None
        self.B = B # 父节点根据此属性值划分产生该节点
        self.X = X
        self.y = y
        self.children = []
        self.A = A
        self.isLeaf = True
        self.label = None
    
    def is_same_label(self):
        return len(list(set(self.y))) == 1
    
    def is_feature_empty(self):
        return len(self.A) == 0
    
    def is_same_features(self):
        return sum(self.X.duplicated()) == len(self.X)-1
    
    def get_majority_label(self):
        y = list(self.y)
        return max(y, key=y.count)

def TreeGenerate(D, A, B=None):
    X, y = parse_Xy(D)
    node = Node(X, y, A, B)
    if node.is_same_label():
        node.isLeaf = True
        node.label = node.y.tolist()[0] 
        return node
    
    if node.is_feature_empty() or node.is_same_features():
        node.isLeaf = True
        node.label = node.get_majority_label()
        return node
    
    node.isLeaf = False
    aStar = get_best_attribute(X, y, A)
    node.optimalAttr = aStar
    
    # 根据属性把数据集进行划分
    Dvs = {}
    for aVal in D[aStar].unique():
        Dvs[aVal] = D[D[aStar].isin([aVal])]
    
    for aVal, subD in Dvs.items():
        subA = set(A) - set(aStar)
        
        subX, suby = parse_Xy(subD)
        if len(subD) == 0:
            subnode = Node(subX, suby, subA)
            subnode.isLeaf = True
            subnode.label = node.get_majority_label()
            node.children.append(subnode)
            return node
        else:
            subnode = TreeGenerate(subD, subA, B=aVal)
            node.children.append(subnode)
    return node

def get_pred_y(x, root):
    while not root.isLeaf:        
        bestAttr = root.optimalAttr   
        xValue = x[bestAttr]
        
        unknown = True # 如果树只用一部分数据集，可能有的新测试样本找不到分支
        for child in root.children:
            if xValue == child.B:
                root = child
                unknown = False
                break
        if unknown:
            break
    if unknown:
        return 'unknown'
    return root.label

7. 实战：车接受率分类

数据集介绍：

来源：Marko Bohanec ，UCI数据集
目的：根据车的购买价格、维护价格、车门数、乘客数等来判断车的接受程度。
属性及取值：本教程中只考虑购买价格（分低、中、高、很高 4 档）和维护价格（分低、中、高、很高 4 档）两个属性。车的接受程度（分不可接受、可接受、好、很好 4 档）。
说明：由于类别不平衡，对原样本的车的 4 种接受程度各取 60 个样本进行试验。

data = pd.read_csv('data/carEvaluation/car.data', header=None)
data.columns = list('abcdefy')

unacc = data.loc[data['y'].isin(['unacc'])].iloc[:60]
acc   = data.loc[data['y'].isin(['acc'])].iloc[:60]
good  = data.loc[data['y'].isin(['good'])].iloc[:60]
vgood = data.loc[data['y'].isin(['vgood'])].iloc[:60]

data = pd.concat([unacc, acc, good, vgood]).reset_index()
print(data.shape)
D = data[list('aby')] # 支取两个变量
A = set(list('ab'))

X, y = parse_Xy(D)

attr2values = {}
for col in X.columns:
    attr2values[col] = list(X[col].unique())
print(attr2values)

root = TreeGenerate(D, A)

# 预测准确率
correct = 0

for i in range(len(X)):
    x = X.iloc[i]
    y1 = y[i]
    y2 = get_pred_y(x, root)
    correct += int(y1 == y2)
    
print(correct / len(X))

# 绘图
aa, bb = np.meshgrid(attr2values['a'], attr2values['b'])
XX = pd.DataFrame({'a':aa.ravel(), 'b':bb.ravel()})

yy = []
for i in range(len(XX)):
    xx = XX.iloc[i]
    yy.append(get_pred_y(xx, root))

# 把字符串映射到数值
amap = {'low':0, 'med':1, 'vhigh':2}
bmap = {'low':0, 'med':1, 'high':2, 'vhigh':3}
ymap = {'unacc':1, 'acc':2, 'good':3, 'vgood':4}

aa2 = np.array([amap[a] for a in aa.ravel()])
bb2 = np.array([bmap[b] for b in bb.ravel()])
yy2 = np.array([ymap[y] for y in yy])

im = np.zeros(aa.shape)
for a2,b2,y2 in zip(aa2,bb2,yy2):
    im[b2,a2] = y2

plt.figure(figsize=(8,6))
plt.imshow(im, cmap=plt.cm.autumn_r)
plt.xticks(list(amap.values()), list(amap.keys()))
plt.xlabel('buying price', fontsize=12)
plt.yticks(list(bmap.values()), list(bmap.keys()))
plt.ylabel('price of the maintenance', fontsize=12)
plt.title('Car acceptability')

for a2,b2,y2 in zip(aa2,bb2,yy2):
    label = list(ymap.keys())[list(ymap.values()).index(y2)]
    plt.text(a2-0.1, b2, label, fontsize=13)

plt.savefig('images/decision_tree_car.png')
plt.show()

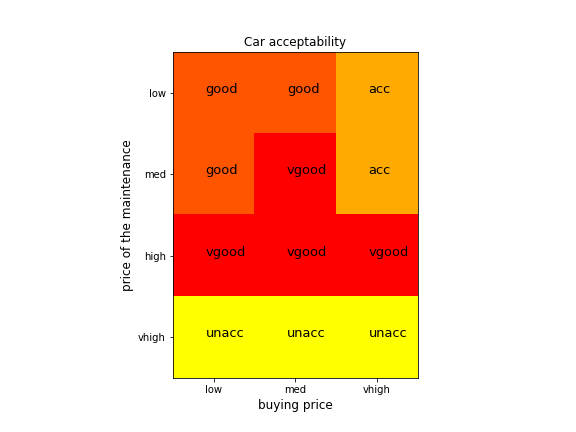
8. 实战：蘑菇是否可食用分类

数据集介绍：

来源： Alfred A. Knopf, Jeff Schlimmer UCI数据集
目的：根据蘑菇的菌盖、菌褶、菌杆的颜色、气味、类型、形状等判断蘑菇是否可食用。
8124个样本。22个属性，每个属性值均为字符串。

data = pd.read_csv('data/mushroom/agaricus-lepiota.data', header=None)
print(f'data.shape = {data.shape}')

data.columns = list('y' + string.ascii_lowercase[:data.shape[1]-1])
# data.shape = (8124, 23)

n = 5000
X_train = data.iloc[:n,1:]
y_train = data.iloc[:n,0]
X_test = data.iloc[n:,1:]
y_test = data.iloc[n:,0]

Dtrain = pd.concat([X_train, y_train], axis=1)

A = data.columns[1:]

attr2values = {}
for col in X_train.columns:
    attr2values[col] = list(X_train[col].unique())

# 训练模型    
root = TreeGenerate(Dtrain, A)

# 预测
correct = 0
for (i, xx), yy in zip(X_test.iterrows(), y_test):
    y2 = get_pred_y(xx, root)
    correct += int(y2 == yy)
    
print('Accurancy =', correct / len(X_test))

9. Sklearn中的决策树

class sklearn.tree.DecisionTreeClassifier(*, criterion='gini',splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort='deprecated', ccp_alpha=0.0)

参数
- criterion [{“gini”, “entropy”}, default=”gini”] 衡量划分质量的方法，使用 gini 时采用基尼不纯度衡量，采用 entropy 时采用信息增益衡量。
- splitter [{“best”, “random”}, default=”best”] 每次分支采用的划分方法，best 为最佳划分（寻找重要度最大的一个属性进行划分），random 为根据特征的重要程度进行随机选择（重要度大的特征被选中的概率高，对基尼重要度进行归一化）。
- max_depth [int, default=None] 树的最大深度
- min_samples_split [int or float, default=2] 一个节点至少要有 min_samples_split 个样本，才进行划分
- min_samples_leaf [int or float, default=1] 划分后子节点至少要有 min_samples_leaf 个样本，才进行划分
- max_features [int, float or {“auto”, “sqrt”, “log2”}, default=None] 寻找最佳划分时候时考虑的特征数
- max_leaf_nodes [int, default=None] 叶节点数最大数量
- min_impurity_decrease [float, default=0.0] 如果进一步划分，不纯度的减少量低于该值，则不进行进一步划分
- min_impurity_split [float, default=0] 在树生长过程种提前停止的阈值，如果一个节点的不纯度小于该阈值，则不进行下一步划分
属性
- classes_ [ndarray of shape (n_classes,) or list of ndarray] 类别标签
- feature_importances_ [ndarray of shape (n_features,)] 特征重要度
- max_features_ [int] 等于输入的参数中的 max_features
- n_features_ [int] 当执行 fit 后的特征后
方法
- fit(X, y[, sample_weight, check_input, . . . ])
- predict(X[, check_input])
- score(X, y[, sample_weight])

from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

data = pd.read_csv('data/mushroom/agaricus-lepiota.data', header=None)
print(data.shape)

encoder = LabelEncoder()
D = pd.DataFrame()

for c in data.columns:
    D[c] = encoder.fit_transform(data[c])

    

X = D.iloc[:, 1:]
y = D.iloc[:, 0]

Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.9, shuffle=True)

# 运行决策树
dtree = DecisionTreeClassifier()
dtree.fit(Xtrain, ytrain)
acc = dtree.score(Xtest, ytest)
print(acc)