二分图

超级详细的基础算法和数据结构合集：
https://blog.youkuaiyun.com/GD_ONE/article/details/104061907

摘要

本文主要介绍二分图的基本概念以及如何用染色法判断二分图，如何用匈牙利算法求二分图的最大匹配。

什么是二分图

二分图又称作二部图，是图论中的一种特殊模型。…（百度百科）
简单来说就是：如果一个图的所有顶点可以被分成左右两个集合，两个集合中不存在任意两点是直接相连的。

如图1所示：

图一

---

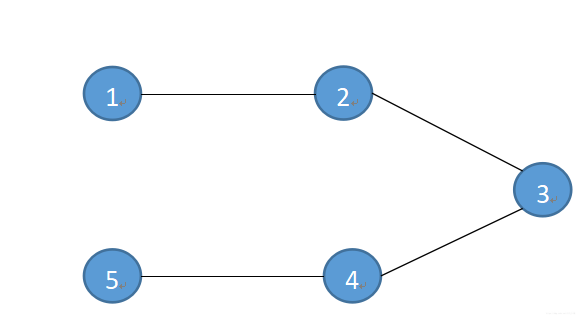
虽然它看起来并不是一个二分图，但是我们可以对图中点的位置进行一些该动。
如图二所示：

图二

---

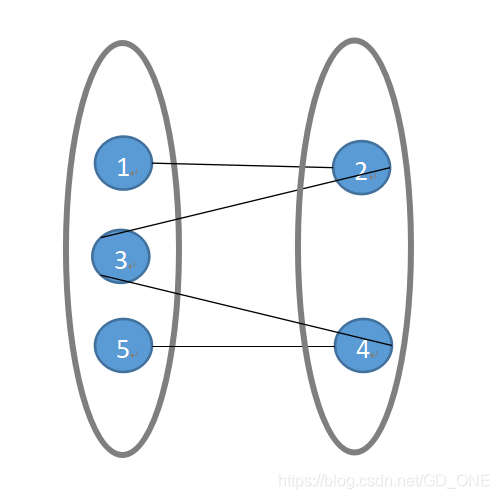
这样看着就直观多了。 135被分为一个点集，24被分为一个点集，并且135之间没有能直接连通的两个点，24中也没有。所以上图就是二分图。
另外，二分图可以是不连通的。

染色法判断二分图

通过二分图的定义我们可以知道，同一个点集中任意两个点之间没有边，也就是说一条边的两个顶点一定不在同一个集合。然后我们可以根据这个性质给每个点设置一个标记，如果一个点标记为1，那么将它的直接后继结点标记为2，如果一个点被标记两次不同的值，那么说明图中存在奇数边的环，该图不是二分图。

更形象的来说，用染色的方式给每个点依次进行染色，如果一个点被染上两种颜色，则该图不是二分图。这就是染色法的由来。

那么为什么存在奇数环时，该图一定不是二分图呢？

如图三所示：

---

图三

---

可以看到2，3，4号点连成了一个奇数环，那么根据定义，2号点和3号点相邻，所以2,3一定在不同的集合，假如2号点在1集合，3号在2集合，那么4号既不能和2号在一个集合也不能和3号在一个集合，此时就矛盾了，构不成二分图。

接下来就是实现代码了：

依次对每个点进行染色，所以我们可以直接对图DFS一遍。如果遇到某个点被染了两次，就结束。说明该图不是二分图。如果所有点都被成功染色，说明该图是二分图。

public static Boolean dfs(int u, int c){// u是当前染色的结点，c是颜色
        color[u] = c;  // 用1和2代表两种颜色，0代表还未染色
        for(int i = h[u]; i != 0; i = ne[i]){
            int j = e[i];
            if(color[j] == 0){//如果u的邻接点e[i]还未染色，则递归对其染色
                dfs(j, 3-c);// 如果u是1， 那么j就是 3-1 = 2， u是2， j就是3-2 = 1
            }
            else if(color[u] == color[j]){//如果u和j的颜色相同，说明u和j在同一个点集内，存在奇数环，该图不是二分图
                return false;
            }
        }
        return true;// 染色成功
    }    

看一道模板题：
染色法判定二分图

代码：

import java.io.*;
import java.util.*;

public class Main{
    static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    static final int N = 2*100010;
    static int[] e = new int[N], ne = new int[N], h = new int[N], color = new int[N];
    static int n, m, idx = 1;
    public static int Int(String s){
        return Integer.parseInt(s);
    }
    
    public static void add(int a, int b){
        e[idx] = b;  ne[idx] = h[a]; h[a] = idx++;
    }
    
    public static Boolean dfs(int u, int c){
        color[u] = c;
        for(int i = h[u]; i != 0; i = ne[i]){
            int j = e[i];
            if(color[j] == 0){
                dfs(j, 3-c);
            }
            else if(color[u] == color[j]){
                return false;
            }
        }
        return true;
    }    
    
    public static void main(String[] agrs) throws Exception{
        String[] s = in.readLine().split(" ");
        n = Int(s[0]);
        m = Int(s[1]);
        
        for(int i = 0; i < m; i++){
            String[] s1 = in.readLine().split(" ");
            int a = Int(s1[0]);
            int b = Int(s1[1]);
            
            add(a, b); add(b, a);
        }
        
        Boolean f = true;
        for(int i = 1; i <= n; i++){// 对每个点都进行染色，防止图是不连通的
            if(color[i] == 0){
                if(!dfs(i, 1)){
                    if(!dfs(i, 2)){
                        f = false;
                        break;
                    }
                }
            }
        }
           
        if(f) out.write("Yes\n");
        else out.write("No\n");
        out.flush();
    }
}

匈牙利算法

匈牙利算法用于求二分图的最大匹配数。

二分图的最大匹配数：

所谓最大匹配数，意思就是求二分图两个点集之间一共有多少直接相连的两两成对的点对。两两成对，跟找对象是一样的，一个点只能有一个对象，不能存在脚踏两只船的情况。

如图四所示：

---

图四

---

对于图四，最大匹配数是2， （1 , 2） 和（3， 4）,5号点没人要，单身。

求最大匹配数，可以看做是给点集1中的点从点集2中找对象，点集1中的点都是男的，点集2中的点都是女的，点集1中的男的都很好说话，只要当前给他介绍的女的是单身，就同意匹配，而且点集1中的男的还很善良，哪怕当前介绍的女孩儿不是单身，只要她对象可以跟她立马分手，他还是可以同意匹配的。

如图五所示：

---

图五

---

1. 先将2号点介绍给1号点， 此时（2，1）匹配，2的男票是1了。（我们只关心女孩有没有对象）

2. 然后轮到给3号点介绍对象了， 3号点和2号点相连，但是问题是2号点此时已经有男朋友了， 不过不要紧，我们来挖强jio，随着渣男语录的强大攻势，2号点和她对象分手了，原因是1号怀疑2号出轨，然后1号就去找6号匹配了。
   最后，皆大欢喜， （2, 3）匹配， （6，1）匹配。

3. 接着，要给5号点介绍对象了，5和6相连，但是6号已经有男朋友了，对，还是1号，那么怎么办呢，虽然5号惊天地泣鬼神的求爱很感人，但6号还是没有和1号分手，原因是1号没有其他的beitai了。因为5号和4号不相连，所以最终5号和4号单身。该图的最大匹配为2。

匈牙利算法就是对以上过程的模拟。
首先用一个数组标记女孩们是否有男朋友。然后遍历点集1中的所有点，给他们介绍对象。对于每一次介绍对象，如果一个女孩被介绍给别人过了，就不在重复介绍。所以还需要一个数组来标记在匹配过程中，女孩是否被介绍过。
具体看代码：

public static Boolean find(int x){
    for(int i = h[x]; i != 0; i = ne[i]){
        int j = e[i];
        if(st[j] == 0){ 
            st[j] = 1;
           //如果女孩j没有男朋友或者女孩j的对象还有其他选择，就将j匹配给x
           if(match[j] == 0 || find(match[j])){
                match[j] = x; 
                return true; // 匹配成功
           }
        }
    }
        return false;
}

然后是例题：
二分图的最大匹配

代码：

import java.io.*;
import java.util.*;

public class Main{
    static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
    static final int N = 100010;
    static int[] e = new int[N], ne = new int[N], h = new int[505], match = new int[N], st = new int[N];
    static int n1, n2, m, idx = 1;
    
    public static int Int(String s){
        return Integer.parseInt(s);
    }
    
    public static void add(int a, int b){
        e[idx] = b;  ne[idx] = h[a]; h[a] = idx++;
    }
     
    public static Boolean find(int x){
        for(int i = h[x]; i != 0; i = ne[i]){
            int j = e[i];
            if(st[j] == 0){
                st[j] = 1;
                
                if(match[j] == 0 || find(match[j])){
                    match[j] = x; 
                    return true; 
                }
            }
        }
        return false;
    }
    
    public static void main(String[] agrs) throws Exception{
        String[] s = in.readLine().split(" ");
        n1 = Int(s[0]);
        n2 = Int(s[1]);
        m = Int(s[2]);
        
        for(int i = 0; i < m; i++){
            String[] s1 = in.readLine().split(" ");
            int a = Int(s1[0]);
            int b = Int(s1[1]);
            add(a, b); 
        }
        
        int res = 0;
        
        for(int i = 1; i <= n1; i++){
            Arrays.fill(st, 0);//每次给一个点匹配对象前都要进行初始化
            if(find(i)) res ++;
        }
       
        out.write(res+"\n");
        out.flush();
    }
}

快去试试你能不能匹配成功吧。yxc说每个点都要尝试匹配一下，哪怕没有结果也不能错过。