一文带你深入了解思维链（CoT）

最新推荐文章于 2025-09-11 11:12:26 发布

原创最新推荐文章于 2025-09-11 11:12:26 发布 · 1.9k 阅读

26 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #语言模型 #思维链

编程人生同时被 2 个专栏收录

14 篇文章

订阅专栏

人工智能

8 篇文章

订阅专栏

引言

随着AI大模型应用的不断深入，如何让 AI 模型在面对复杂问题时不仅给出答案，还能清晰展示思考过程成为了研究热点。思维链（Chain-of-Thought, CoT）技术正是为了解决这一难题而提出的——它通过逐步拆解问题、生成推理步骤，将“黑盒”模型转变为具有可解释性的推理系统。

思维链（Chain of Thought，CoT），是AI大模型技术领域一个全新的AI技术概念。其强大的逻辑推理是大语言模型“智能涌现”出的核心能力之一，就好像AI有了人的自主意识一样。而它推理能力的关键在于——思维链（Chain of Thought，CoT）。

在解决复杂问题时（例如数学推理），AI大模型很难直接给出我们想要的答案。而思维链（CoT）则通过要求/提示模型在输出最终答案之前，显式输出中间逐步的推理步骤这一方法来增强AI大模型的算数、常识和推理的质量。思维链（CoT）大幅度提高了 LLM（大语言模型）在复杂推理任务上的性能，并且输出的中间步骤方便用户了解AI大模型的思考过程，提高了大模型推理的可解释性。

1.什么是思维链（CoT）

1.1 导入

在介绍思维链之前，我们先了解一下什么是语言智能，语言智能与思维链有何关联。

语言智能（Linguistic Intelligence）通常指“利用语言符号进行理解、表达、推理与创造”的综合能力。在人工智能语境下，它特指大模型所展现的**“语言驱动”的通用智能**：

理解：解析文本、语音、代码等多模态符号；
推理：在符号内部或跨符号之间完成逻辑、数学、常识、情境等多类型推理；
创造：生成连贯、符合目标的新符号序列（写作、对话、代码、摘要等）。

因此，语言智能 = 语言理解 + 语言推理 + 语言生成的闭环。

随着AI大模型参数量的飞升，以 Transformer 为基础架构的大规模语言模型以 “对话” 的方式逐渐展现出了强大的理解与推理的能力。大模型逼近“语言智能”是其概念推理能力。推理，一般指根据几个已知的前提推导得出新的结论的过程。区别于语言理解，推理一般是一个“多步骤”的过程，推理的过程可以形成非常必要的“中间概念”，这些中间概念将辅助复杂问题的求解。

大模型推理

1.2 传统推理存在的局限性

在传统大模型推理流程中，传统推理通常一步到位，模型通常只给出最终答案，而忽略了中间推理步骤的展示。

这个“一步到位”范式在简单任务上表现良好，但在需要多步逻辑、数值计算或跨知识整合的场景中暴露出四大核心问题：隐式、跳步、幻觉、不可干预。

“一步到位”的大模型在复杂推理任务上既不够准，也不可信，这种设计存在以下问题：

可解释性差：用户无法了解模型如何从输入信息推导出答案，尤其在数学计算、编程问题等需要精细逻辑推理的场景中，这种“黑盒”操作会导致用户对模型决策失去信任。
错误率较高：缺乏明确的中间步骤会使模型在推理过程中出现跳跃性错误，遗漏关键步骤，从而导致最终答案出现偏差。
适应性不足:在多条件决策、跨领域任务等复杂场景中，模型难以灵活调整推理路径，无法同时兼顾所有逻辑因素，影响决策的鲁棒性。

思维链把推理拆成“多步可检查”，从而同时提升准确率、可解释性和可控性。

准确率瓶颈
多跳数学、医学诊断、法律条文适用等问题往往需要环环相扣的中间结论；一次性输出答案相当于要求模型在 1 个 token 里完成 10 步计算，错误率随步骤指数级上升。思维链显式写出中间结果，让每一步都有机会被验证或纠正，整体错误率显著下降（GSM8K 数学任务提升 20-40%）。
可解释性与合规需求
金融风控、医疗诊断、司法判决等场景必须给出“为什么这么做”。思维链把推理过程白盒化，方便人类审计、监管审查，满足 GDPR、HIPAA 等法规要求。
可控与可干预
当用户或专家发现某一步有问题时，可直接修改该步并重新生成后续推理，实现“人在回路”的实时纠错；没有思维链，只能整体重跑整个黑箱。

思维链不是为了“让模型更聪明”，而是通过结构化的逐步显式推理，把大模型从“高概率猜答案”升级为可验证、可修正、可教学的推理系统，这也是AI大模型为什么需要引入思维链的根本原因。

1.3 什么是思维链（CoT）

AI大模型的 “思维链”（Chain of Thought, CoT） 是一种通过模拟人类逐步推理过程来提升模型复杂问题解决能力的技术。思维链（CoT）就是一系列中间的推理步骤，通过让大模型逐步参与将一个复杂问题分解为一步一步的子问题并依次进行求解的过程，其核心是让模型在输出最终答案前，显式生成中间的逻辑步骤，而非直接给出结论。

这一概念由Google在2022年提出（论文《Chain-of-Thought Prompting Elicits Reasoning in Large Language Models》），现已成为大模型推理的核心方法之一。思维链的提出标志着大模型从“直觉回答”向“逻辑推演”的进化，成为提升AI可靠性的关键技术之一。

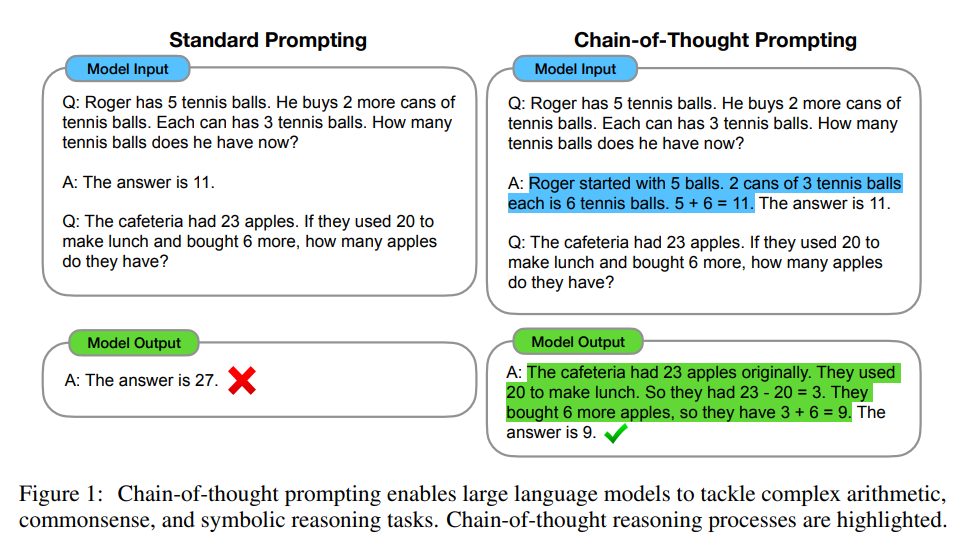
思维链提示词

区别于传统的提示词工程（Prompt）从输入直接到输出的映射 input——>output的方式，思维链（CoT）完成了从输入到思维链再到输出的映射，即 input——>reasoning chain——>output。如果将使用思维链（CoT）的 Prompt 进行分解，可以更加详细的观察到思维链（CoT）的工作流程。

思维链工作流程

一个完整的包含 CoT 的 Prompt 往往由 指令（Instruction），逻辑依据（Rationale），示例（Exemplars） 三部分组成。

指令（Instruction）：用于描述问题并且告知大模型的输出格式；
逻辑依据（Rationale）：指 CoT 的中间推理过程，可以包含问题的解决方案、中间推理步骤以及与问题相关的任何外部知识；
示例（Exemplars）：指以少样本的方式为大模型提供输入输出对的基本格式，每一个示例都包含：问题，推理过程与答案。

思维链（CoT）大幅度提高了 LLM 在复杂推理任务上的表现，并且输出的中间步骤方便使用者了解模型的思考过程，提高了大模型推理的可解释性。目前，思维链推理已经成为大模型处理复杂任务的一个常用手段。

（1）语言智能与思维链的关系

语言智能提供了“能用语言思考”的通用底座；思维链是把语言智能的推理过程显式化、步骤化、可验证化的技术手段，两者呈“底座”与“增强插件”的关系。

语言智能是底座：提供强大的符号表征、记忆与生成能力；
思维链是增强插件：在底座的基础上的“一次性爆发”拆成多步、可显式、可检查的连续输出，使复杂推理任务可以被逐步驱动、实时纠偏。

维度	语言智能	思维链（CoT）	关系说明
能力范围	广谱语言任务	多步逻辑/数值/决策任务	CoT 是语言智能在复杂推理子集上的显式化
输出形态	直接答案	中间步骤+最终答案	CoT 把隐式推理变成显式草稿
可控性	黑箱	白盒可干预	CoT 提升语言智能的可解释性与可修正性
性能增益	基线	+10~40%	CoT 通过分解-自洽机制放大语言智能在困难任务上的有效容量

（2）思维链如何解决传统大模型推理的局限性

传统大模型像“闭卷口算”，思维链（CoT）把它变成“开卷列式”——写草稿、可验算、能改错，从根本上解决了隐式、跳步、幻觉、不可干预四大硬伤。

局限 1：隐式推理 → 黑箱不可解释
- 现象
  模型直接吐出结果，无法展示中间推导，医生/法官/风控人员无法复核。
- CoT 解法
  显式生成中间步骤，把黑箱拆成“白盒草稿”，每一步都可人工检查或修改。
局限 2：跳步误差 → 复杂任务准确率骤降
- 现象
  数学、医学诊断等多跳问题，错误率随推理步数指数级累积。
CoT 解法
将长链拆成若干子问题，显式缓存每一步结果，误差从“乘性”降为“加性”，整体准确率提升 20-40%。
局限 3：缺乏自洽校验 → 幻觉频发
- 现象
  同一 prompt 多次采样可能给出矛盾答案，模型自己意识不到。
- CoT 解法
  Self-Consistency：生成多条思维链后投票或打分，选出最一致答案，显著降低幻觉。
局限 4：不可干预 → 出错只能重跑
- 现象
  用户发现答案有误，却无法定位并修正中间环节，只能整体重试。
- CoT 解法
  支持“人在回路”干预：用户直接修改某一步，模型基于修改后的上下文继续生成后续步骤，实现局部重算。

传统局限	根因	CoT机制	效果
黑箱不可解释	隐式推理	显式中间步骤	可审计、可教学
跳步误差高	一次性解码	分步缓存	准确率↑20-40%
幻觉	无自洽	多条链投票	一致性↑
不可干预	无草稿	可修改单步	实时纠错

1.4 思维链（CoT）的作用

提升复杂推理能力
通过分步拆解问题（如数学计算、逻辑谜题），模型能更准确地处理多跳推理（multi-hop reasoning）。例如：
问题：“小明有15个苹果，吃了3个，又买了5个，现在有多少？”
思维链：
- 初始苹果：15
- 吃掉后：15 - 3 = 12
- 购买后：12 + 5 = 17
  最终答案：17
增强可解释性
中间步骤让用户能验证模型的逻辑是否合理，而非仅依赖“黑箱”输出。
减少幻觉（Hallucination）
显式推理过程迫使模型基于已知信息推导，降低凭空编造答案的概率。
适应少样本学习（Few-shot Learning）
在提示（prompt）中提供少量带思维链的示例，即可引导模型模仿这种推理模式，无需额外训练。

1.5 思维链（CoT）的局限性

思维链（CoT）虽然大幅提升了大模型在复杂推理任务上的表现，但它并非万能钥匙，仍存在多重局限。

CoT 的效果高度依赖模型的规模：在百亿参数以下的小模型中，生成连贯且逻辑严密的中间步骤往往力不从心，导致链式推理反而变成“链式胡言”。
计算成本高：显式地写出每一步会显著增加输出长度，推理延迟和算力成本随之线性或超线性上升，对实时性要求高的场景并不友好。
错误累积：CoT 并不能完全消除幻觉，只是将幻觉从“最终答案”前移到“中间步骤”；如果某一步骤出现事实或逻辑错误，后续链式推导会继续放大偏差，缺乏自我校正机制。
对输入措辞敏感：链式结构对输入措辞极度敏感——同一个问题换一句说法，就可能触发截然不同的推理路径，稳定性不足。
限制创意发散：对于主观性强、价值判断重或缺乏明确可验证步骤的任务（如诗歌创作、伦理决策），CoT 的“逐步解释”不仅难以给出客观标准，还可能限制创意发散。
可追溯性有限：CoT 的可解释性只是“看起来透明”，其每一步依旧基于概率生成，而非符号逻辑，真正的因果可追溯性仍然有限；当监管或审计要求“每一步都可数学证明”时，它依旧无法满足。

2.为什么要用思维链（CoT）

自思维链（Chain-of-Thought, CoT）技术问世以来，其对大语言模型（LLM）能力的赋能作用已被大量研究充分验证。这一技术之所以成为大模型推理领域的关键突破，核心在于它直击了大模型在复杂任务处理中存在的固有局限，为提升模型性能提供了系统性解决方案。若深入剖析其核心价值，可归纳为以下四个维度，而这些维度恰恰回答了“为何AI大模型需要思维链”这一根本问题：

2.1 突破复杂推理瓶颈，显著增强大模型的问题求解能力

大模型在处理需要多步逻辑推演的复杂任务时，若直接输出答案，往往因信息处理跨度太大而出现逻辑断裂、关键细节遗漏等问题。思维链的核心价值在于将人类解决复杂问题的认知模式赋予模型——通过引导模型将宏观问题拆解为一系列连续的子问题与中间步骤，迫使模型在每一步骤中聚焦具体逻辑节点。这种“分而治之”的策略不仅降低了单次推理的认知负荷，更确保了模型对问题的每个关键环节都进行充分计算，避免了因“一步到位”的思维跳跃而导致的疏漏。从资源分配角度看，思维链使模型的计算资源能精准投向问题的核心推理步骤，而非在无关信息中浪费算力，从而从本质上提升了复杂任务的求解准确率。

2.2 破解“黑箱”困境，大幅提升大模型的可解释性

大模型的“黑箱特性”一直是其在高风险领域应用的主要障碍——当模型仅输出最终答案时，人类无法追溯其决策依据，既难以判断结果的可靠性，也无法定位错误根源。思维链通过显性化模型的推理路径，将“做题过程”完整呈现，使人类能够清晰观察模型如何从已知条件出发，通过一步步逻辑推导抵达结论。这种透明化的过程不仅让结果的可信度可被验证（例如判断每一步推理是否符合常识或逻辑规则），更为错误分析提供了具体抓手：若最终答案出错，可通过回溯中间步骤定位是前提理解偏差、逻辑规则误用还是计算失误，从而为模型优化提供明确方向。

2.3 实现过程性干预，有效增强对大模型的可控性

在没有思维链的场景中，大模型的推理过程完全隐藏在“输入-输出”的黑箱中，人类无法对其决策路径施加影响，一旦模型出现偏离预期的推理倾向，难以实时纠偏。而思维链通过将推理过程转化为可观测、可干预的步骤序列，使人类能够在模型的推理环节中嵌入引导性信息。例如，当发现模型某一步骤出现逻辑偏差时，可通过补充提示修正其思路；对于高风险任务（如医疗诊断、金融分析），还可通过校验中间步骤的合理性，提前规避错误结论的输出。这种“过程可控性”是大模型从实验室走向实际应用的关键前提，避免了模型成为完全不可控的“黑箱工具”。

2.4 具备普适性与扩展性，极大提升大模型的应用灵活性

大模型的技术迭代需要兼顾性能提升与落地成本，而思维链的“轻量化”特性使其具备极强的实用价值：一方面，它无需对模型架构进行大规模改造，仅通过在提示词中添加“让我们一步一步思考”（Let’s think step by step）等引导语，即可在各类大模型中快速部署，大幅降低了技术应用的门槛；另一方面，思维链赋予模型的“分步推理能力”并非局限于语言类任务，在科学计算（如数学公式推导）、逻辑推演（如符号推理）、智能体（AI Agent）决策（如多任务规划）等跨领域场景中均能发挥作用，这种跨任务适配性使其成为赋能大模型泛化能力的核心工具。

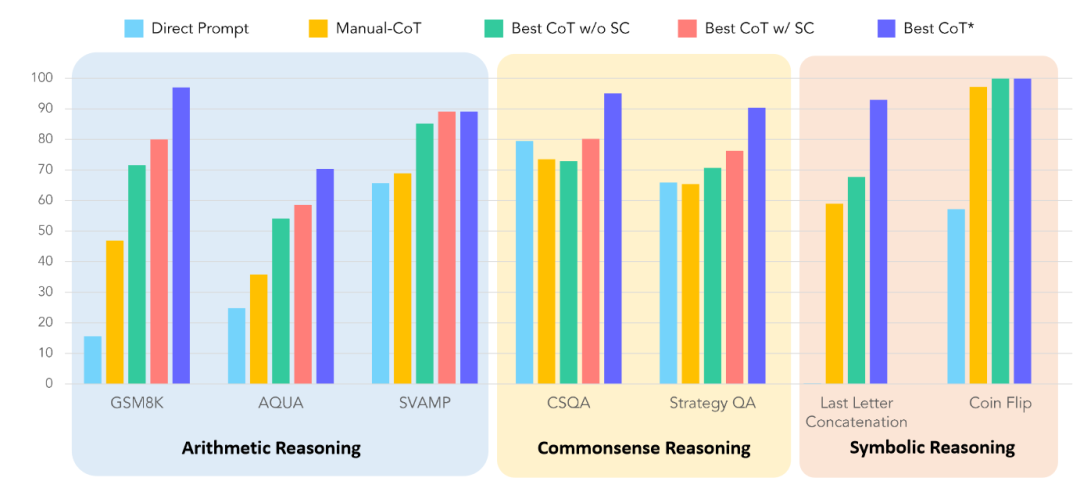
从实证角度看，思维链（CoT）在七个涵盖算术推理、常识推理、逻辑推理等不同类型的任务数据集上的实验结果进一步印证了思维链的普适价值：相较于直接输出答案的传统提示方式，思维链在所有任务中均带来了统计意义上的显著性能提升。这一结果不仅证明了思维链对模型能力的增强效果，更揭示了其作为一种“通用推理框架”的核心价值——它通过模拟人类认知的自然逻辑，填补了大模型从“信息处理”到“逻辑推理”的能力鸿沟，最终让大模型在复杂世界的问题解决中更接近人类的智能水平。

CoT推理任务提升

3. 思维链（CoT）的核心原理与推理机制

3.1 核心原理

思维链（Chain-of-Thought，CoT）的核心原理，本质上是通过模拟人类解决复杂问题的自然认知规律，将原本需要一次性完成的、隐性的长程推理过程，系统性拆解为一系列连续且可追踪的中间步骤。这些步骤既不是孤立的片段，也不是随机的罗列，而是遵循逻辑递进关系的 “推理链条”—— 前一步的结论成为后一步的前提，最终形成从问题初始条件到最终答案的完整路径。

从技术实现的角度看，这一过程的关键在于将模型内部隐性的思维活动转化为显式的文本输出：每个中间步骤都清晰呈现模型对信息的加工过程（如 “已知 A 和 B，可推出 C”“这里需要验证 C 是否符合前提 D”），使原本黑箱中的逻辑推演变得可观测。同时，这些步骤具备双重特性：

一方面，它们是 “可验证的”—— 每一步都能独立接受逻辑规则、常识或领域知识的检验，判断其合理性；
另一方面，它们是 “可纠错的”—— 若某一步出现偏差，可通过修正该节点直接调整后续推理方向，避免错误在链条中持续传递。

而这种拆解对语言模型的核心价值，正如 “自己给自己写草稿” 的生动比喻：在解码阶段（即模型生成答案的过程中），分步推理为模型提供了 “缓冲带”—— 就像人类演算时会在草稿纸上记录中间结果以减轻记忆负担，模型通过输出中间步骤，能够阶段性 “锚定” 已处理的信息，避免因推理链条过长导致的关键细节丢失或逻辑断裂。最终，这种机制让模型突破了 “一步到位” 式推理的局限，在复杂任务中实现更稳定、更可靠的逻辑推演。

关键词	技术含义	直观类比
分解（Decomposition）	把整体问题拆成子问题序列	像医生先问诊→体检→化验→诊断，而不是直接给病名
显式化（Explicitation）	每步结果用自然语言写在上下文中	相当于“边算边写草稿”，后续 token 能看到前面所有草稿
自洽（Self-consistency）	多采样多条链，投票或打分取最一致答案	同一道题做 5 次，选出现次数最多的结论
可干预（Intervention）	用户可在任意中间步修改，模型实时重算	像老师把草稿里某行公式改了，学生接着往下算

3.2 推理机制

（一）单条思维链的解码流程

与“人在黑板上写推导流程”完全同构，每一步都基于“自己刚写下的步骤草稿”继续向下推理。

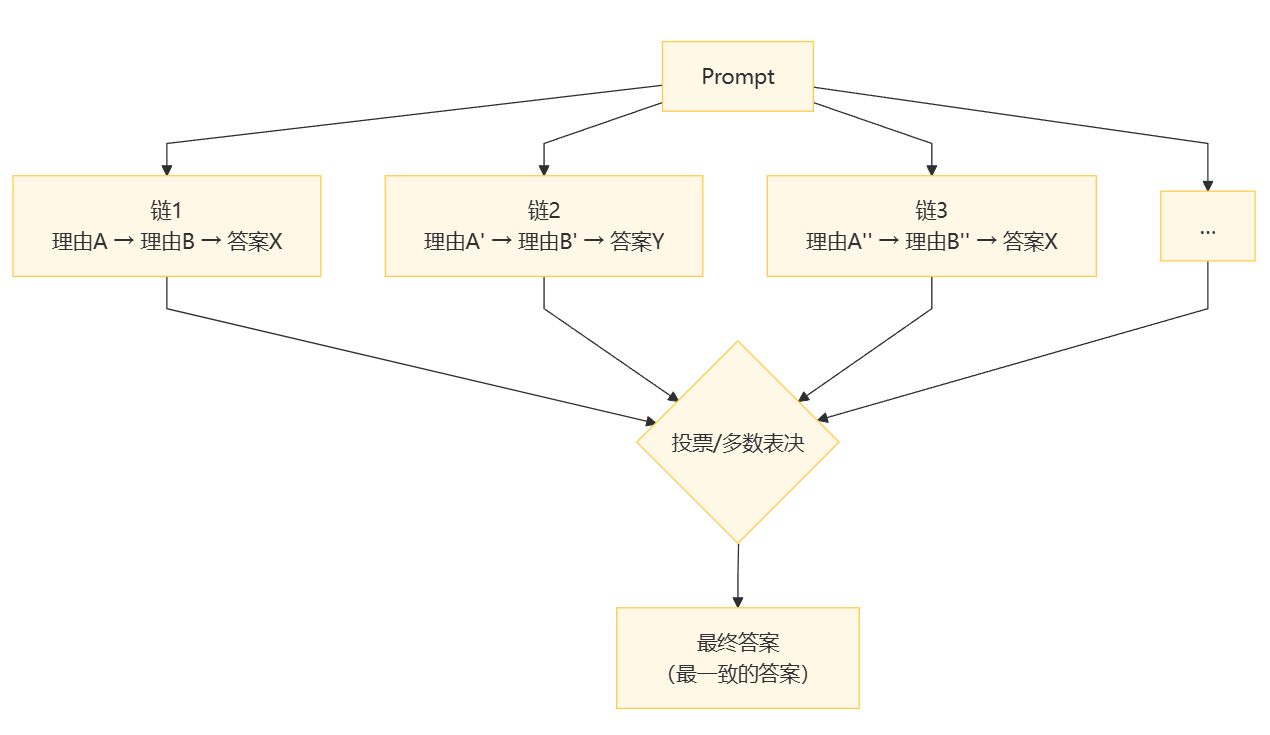
（二）多条思维链的自洽投票

取出现频率最高的最终答案（Self-Consistency），可再对每条链进行权重打分（Weighted CoT），投票表决得出一致的答案。

自洽投票（Self-Consistency）多条 CoT 链示意图

4. 思维链（CoT）解决什么样的问题

思维链（Chain of Thought, CoT）并不是“万能钥匙”，它只在特定类型的问题上能显著提效。根据研究论文（《Chain-of-Thought Prompting Elicits Reasoning in Large Language Models》）研究结果和大量实测经验，它的最佳适用域可归纳为以下四类问题：

思维链适用领域

4.1 多步骤逻辑推理问题

特征：需要连续 2 步以上、且步骤间有因果/数值依赖。
典型例子：

数学应用题
“火车 A 以 60 km/h 先行 2 小时，火车 B 以 80 km/h 追赶，多久追上？”（需：计算先行距离→列追及方程→求解）
逻辑谜题
“甲说乙在撒谎，乙说丙在撒谎，丙说甲乙至少一人说真话，谁在说真话？”（需：逐人设真/假→矛盾检验）

为什么 CoT 有效：显式拆解步骤可避免“跳步”导致的连锁错误。

4.2 知识密集型多跳问答

特征：需整合多个分散信息点，且信息点之间无直接显式关联。
典型例子：

医学诊断
“患者发热+皮疹+近期露营史，可能病因？”（需：关联症状→匹配疾病→排除干扰项）
法律案例推理
“A 在 B 国犯罪后逃至 C 国，引渡需满足哪些条件？”（需：查 B/C 国法律→国际条约→程序步骤）

为什么 CoT 有效：把“隐性知识检索”变成“显式知识链”，降低遗漏关键信息的风险。

4.3 符号操作与计算问题

特征：涉及数值、变量、符号的精确操作，且对顺序敏感。
典型例子：

代数方程
“解方程：3(x+2) - 5 = 2(x-1) + 7”（需：展开→移项→合并同类项→求解）
代码调试
“为何这段 Python 代码输出空列表？”（需：逐行跟踪变量值→定位逻辑漏洞）

为什么 CoT 有效：逐步展开计算过程，使符号操作透明化，减少“口算”错误。

4.4. 需要解释“为什么”的问题

特征：答案本身不是终点，用户需要理解推理依据。
典型例子：

科学解释
“为什么天空是蓝色的？”（需：瑞利散射→波长依赖→人眼感知）
伦理决策
“自动驾驶汽车应优先保护乘客还是行人？”（需：伦理原则→场景权衡→政策依据）

为什么 CoT 有效：显式因果链让用户可验证逻辑，避免“黑箱”答案。

4.5 思维链（CoT）不擅长的领域

单步事实检索
“珠穆朗玛峰多高？”（直接检索即可，CoT 反而冗余）
创造性生成
“写一首关于月亮的诗”（发散性任务，逻辑链可能限制创意）
感知类任务
图像识别、语音识别等（非符号化推理，CoT 无意义）

思维链 = 逻辑链 + 知识链 + 计算链，适用于**“步骤多、信息散、需验证”的问题，但对“单点答案、创意生成、感知任务”**无效。

5. 思维链（CoT）的应用场景

思维链（CoT）把“一步答案”变成“可检查的过程”，因此在任何需要透明、可追责、可教学的复杂推理场景都有落地价值；其边界是：小模型无法驾驭，简单任务无需使用。思维链（Chain-of-Thought, CoT）已被成功应用到数学推理、教育、医疗、法律、金融、科研、内容创作、对话系统等 10 余个垂直领域，核心作用是“把复杂任务拆成可验证的中间步骤”。下面按场景举例说明其典型落地方式。

5.1 医疗健康

任务：辅助诊断 & 病例分析

做法：把主诉、体征、化验结果逐条列出 → 按“鉴别诊断-排除-确诊”链条给出每一步的理由。
示例：Med-PaLM 用 CoT 回答“65 岁男性，胸痛 30 min，ST 段抬高，肌钙蛋白↑，最可能诊断？”会显式列出：
1. 急性冠脉综合征 → 2) 结合 ST 段抬高定位前壁 → 3) 肌钙蛋白支持 STEMI → 结论：立即 PCI。

5.2 法律与合规

任务：条文检索 + 案例比对 + 判决预测

做法：先定位适用法条 → 比对先例 → 评估证据链强度 → 给出风险等级。
示例：律师输入“员工泄露商业秘密，但未签保密协议，能否索赔？”CoT 模型会：
1. 检索《反不正当竞争法》第 9 条 → 2) 找 3 个未签协议仍判赔的案例 → 3) 对比证据 → 结论：可尝试“默示保密义务”路径。

5.3 金融风控

任务：信贷审批 / 欺诈检测

做法：把征信、流水、行为数据分段解读 → 计算违约概率 → 标注关键风险点。
示例：模型审批小微企业贷款时，按“现金流覆盖率<1 → 行业下行 → 抵押物贬值”链条解释拒贷原因，便于客户经理复核。

5.4 科学研究

任务：实验设计 & 机制推断

做法：输入现象 → 提出假设 → 设计验证实验 → 预测结果。
示例：化学家用 CoT 让模型推测“反应产率低”原因：
1. 检查副反应路径 → 2) 计算活化能 → 3) 建议更换催化剂并给出参考文献。

5.5 教育与培训

任务：自动讲题 & 作文批改

做法：按“审题-列式-求解-验算”模板生成逐步解析；作文按“立意-结构-论据-语言”四步点评。
示例：Khan Academy 的 Khanmigo 用 CoT 为学生提供数学题分步提示，而非直接给答案，提高学习留存率。

5.6 对话与客户服务

任务：复杂投诉处理

做法：把用户诉求 → 政策核查 → 可行方案 → 补偿计算逐条呈现。
示例：航空公司客服机器人用 CoT 处理“航班取消+转机错过”：
1. 确认天气属不可抗力 → 2) 计算转机差价 → 3) 提供改签或赔偿选项，减少人工介入。

5.7 内容创作与摘要

任务：长文摘要 / 跨语言报道

做法：先提取主题句 → 归纳要点 → 重组段落 → 生成最终摘要。
示例：SumCoT 框架在多文档摘要中，先列出每篇核心论点，再融合成一条连贯摘要，避免信息丢失。

5.8 程序合成与调试

任务：自动代码生成

做法：自然语言需求 → 伪代码 → 逐行翻译 → 单元测试。
示例：GitHub Copilot 的“CoT 模式”可展示“需求→算法思路→代码→测试用例”四步，方便开发者审查。

5.9 多模态场景

任务：图文混合推理

做法：图像特征 → 文本描述 → 逻辑推理 → 结论。
示例：MM-CoT 让模型看 X 光片后，按“影像表现→可能病灶→下一步检查”链条给出诊断建议，实现“看图说话+推理”。

6. 思维链（CoT）应用示例

在解决数学问题时，思维链（CoT）的核心作用是 把「一步算出答案」变成「多步显式推导」。下面用一个具体例子，拆解它的五步应用流程：

6.1 示例题目和步骤

小明买书花了 120 元，比买笔多花了 40 元，买笔的钱是买本子钱的 3 倍。问买本子花了多少钱？

（1）CoT 的 5 步操作**

Step 1：拆解题目 → 提取已知量

根据题目，已知：
- 买书 = 120 元
- 买书比买笔多 40 元 → 买书 = 买笔 + 40
- 买笔的钱 = 3 × 买本子的钱

Step 2：逆向推导 → 设未知数

设买本子花了 x 元，则：
- 买笔的钱 = 3x 元
- 买书的钱 = 3x + 40 元

Step 3：列方程 → 匹配已知条件

题目说买书花了 120 元，所以：
3x + 40 = 120

Step 4：解方程 → 逐步计算

3x = 120 - 40  
3x = 80  
x = 80 / 3 ≈ 26.67 元

Step 5：验证答案 → 反向代入

买本子 = 26.67 元  
买笔 = 3 × 26.67 ≈ 80 元  
买书 = 80 + 40 = 120 元（匹配题目）

（2）如何用 CoT 提示触发？**

零样本提示（Zero-shot CoT）

Prompt：
“小明买书花了 120 元，比买笔多花了 40 元，买笔的钱是买本子钱的 3 倍。问买本子花了多少钱？让我们一步步思考。”

少样本提示（Few-shot CoT）

提供 1 个类似问题的分步解答作为示例，再提问新问题（模型会模仿格式）。

类似问题示例

（3）为什么 CoT 比直接计算更可靠？

避免跳步错误：如直接写「120 - 40 = 80 元是买笔的钱」会漏掉「3 倍关系」。
可调试：若某一步错误（如误将 3x 写成 x/3），用户能直接定位问题步骤。
适应复杂题型：对「行程问题」「鸡兔同笼」等需多条件整合的题目尤其有效。

6.2 代码示例（使用 OpenAI API）

import openai

response = openai.ChatCompletion.create(
  model="gpt-4",
  messages=[
    {"role": "user", "content": 
     "解数学题：小明买书花了120元，比买笔多花了40元，买笔的钱是买本子钱的3倍。问买本子花了多少钱？请逐步思考并给出每一步的理由。"}
  ]
)
print(response.choices[0].message.content)