图像的几何矩特征

1. 矩的概念

图像识别的一个核心问题是图像的特征提取，简单描述即为用一组简单的数据（图像描述量）来描述整个图像，这组数据越简单越有代表性越好。良好的特征不受光线、噪点、几何形变的干扰。图像识别发展几十年，不断有新的特征提出，而图像不变矩就是其中一个。

矩是概率与统计中的一个概念，是随机变量的一种数字特征。设为随机变量，为常数，为正整数。则量称为关于点的阶矩。

比较重要的有两种情况：

1. 。这时称为的阶原点矩

2. 。这时称为的阶中心矩。

一阶原点矩就是期望。一阶中心矩，二阶中心矩就是的方差。在统计学上，高于4阶的矩极少使用。可以去衡量分布是否有偏。可以去衡量分布（密度）在均值附近的陡峭程度如何。

针对于一幅图像，我们把像素的坐标看成是一个二维随机变量，那么一幅灰度图像可以用二维灰度密度函数来表示，因此可以用矩来描述灰度图像的特征。

不变矩(Invariant Moments)是一处高度浓缩的图像特征，具有平移、灰度、尺度、旋转不变性。M.K.Hu在1961年首先提出了不变矩的概念。1979年M.R.Teague根据正交多项式理论提出了Zernike矩。下面主要介绍这两种矩特征的算法原理与实现。

2. Hu矩(几何矩)

一幅M×N的数字图像f(i,j)，其阶几何矩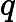mpq和中心矩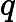为：

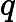
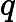
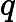
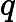
其中f(i,j)为图像在坐标点(i,j)处的灰度值。

若将看作是图像的灰度质量，则为图像的质心坐标，那么中心矩反映的是图像灰度相对于其灰度质心的分布情况。可以用几何矩来表示中心矩，0~3阶中心矩与几何矩的关系如下：

为了消除图像比例变化带来的影响，定义规格化中心矩如下：

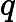
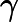
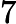
利用二阶和三阶规格中心矩可以导出下面7个不变矩组，它们在图像平移、旋转和比例变化时保持不变。

3. 利用OpenCV计算Hu矩

opencv里对Hu矩的计算有直接的API，它分为了两个函数：moments()函数用于计算中心矩，HuMoments函数用于由中心矩计算Hu矩。

Moments moments(InputArray array, bool binaryImage=false )

参数说明

• 输入参数：array是一幅单通道，8-bits的图像，或一个二维浮点数组(Point of Point2f)。binaryImage用来指示输出图像是否为一幅二值图像，如果是二值图像，则图像中所有非0像素看作为1进行计算。
• 输出参数：moments是一个类：

class Moments
{
public:
    Moments();
    Moments(double m00, double m10, double m01, double m20, double m11,
            double m02, double m30, double m21, double m12, double m03 );
    Moments( const CvMoments& moments );
    operator CvMoments() const;
}

里面保存了图像的2阶与3阶中心矩的值。

void HuMoments(const Moments& moments, double* hu)

参数说明：

• 输入参数：moments即为上面一个函数计算得到的moments类型。
• 输出参数：hu是一个含有7个数的数组。

int main(int argc, char** argv) 
{ 
    Mat image = imread(argv[1]);  
    cvtColor(image, image, CV_BGR2GRAY); 
    Moments mts = moments(image); 
    double hu[7]; 
    HuMoments(mts, hu); 
    for (int i=0; i<7; i++) 
    { 
        cout << log(abs(hu[i])) <<endl; 
    } 
   return 0; 
}