【机器学习】3.决策树

基本流程

输入：训练集 D = {(x₁,y₁),(x₂,y₂),…,(x_m ,y_m)}
   属性集A={a₁,a₂ ,…,a_d}
过程：函数TreeGenerate(D,A)
   1. 生成结点 node；
   2. if D中的样本全属于同一个类别C，then：
   3.   将node作为C类叶节点，return
   4. end if
   5. if A != [] or D中的样本在A上的取值相同，then：
   6.   将node作为也叶结点，其类别为D中样本最多的类，return；
   7. end if
   8. 从A中选择最有划分属性a_*
   9. for a_* 的每一个值 a_*^v, do
   10.   为node生成一个分支，令D_v 表示D在 a_* 上取值为a_*^v的样本子例
   11.   if D_V为空，then
   12.      将分支结点作为叶结点，其类别为D中样本最多的类别，return
   13.   else：
   14.      以TreeGenerate（D_v ，A{a_* }）为分支结点
   15.   end if
   16. end for

从基本流程中可以看出，决策树算法的关键在第8行，如何选择最优划分属性。

划分选择

信息增益

信息增益是度量样本集合纯度最常用的一种指标，假设当前样本D中第k类样本所占的比例为P_K ,则D的信息熵定义为：
$$Ent(D)=-\sum _{k=1}^{|y|}{P}_{k}lo{g}_2{P}_k$$
它的曲线如下：
                  
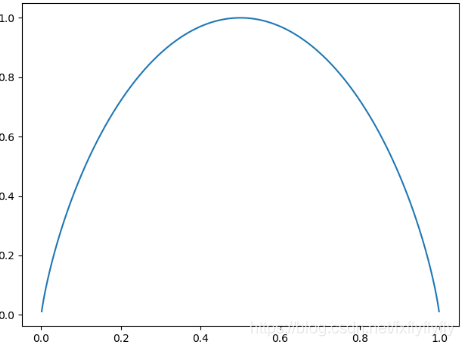
可以看出在概率p=0.5是信息增益最大，为1。我们可以把信息熵理解为“不确定性”，当概率为0.5时，比如抛硬币，出现正反两面的概率都是0.5，所以这个事件的不确定性是最大的；当一个事件发生的概率为0或1的时候，那这个事件就是必然事件了，不确定性为0，所以信息熵最低，为0

假设离散属性a有V个可能的取值{a¹ ,a¹ ,…,a^v },若使用a对样本D进行划分，则会产生V个分支结点，其中第v个分支结点包含了D中所有在属性a上取值为a^v 的样本，记为D^v ，给分支结点赋予权重$\frac{|D^v|}{|D|}$ ,则信息增益为：
$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)$$
可以看出信息增益越大，使用属性a来进行划分的纯度提高越大

编号	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	是
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	是
4	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	是
5	浅白	蜷缩	浊响	清晰	凹陷	硬滑	是
6	青绿	稍蜷	浊响	清晰	稍凹	软粘	是
7	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	是
8	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	是
9	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	否
10	青绿	硬挺	清脆	清晰	平坦	软粘	否
11	浅白	硬挺	清脆	模糊	平坦	硬滑	否
12	浅白	蜷缩	浊响	模糊	平坦	软粘	否
13	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	否
14	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	否
15	乌黑	稍蜷	浊响	清晰	稍凹	软粘	否
16	浅白	蜷缩	浊响	模糊	平坦	硬滑	否
17	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	否

在上表中，根结点包含D中所有样例，正例P₁ =8/17 ，反例P₂ =9/17
$$Ent(D)=-\sum _{k=1}^2{P}_{k}lo{g}_2{P}_k=-(\frac{8}{17}lo{g}_2\frac{8}{17}+\frac{9}{17}lo{g}_2\frac{9}{17})$$
计算当前属性集合{色泽,根蒂,敲声,纹理,脐部,触感}中每一个属性的信息增益，以色泽为例，它有三个取值：{青绿，乌黑，浅白}，若以色泽进行划分，可得到三个子集。
   D¹(青绿)={1，4，6，10，13，17} 其中正例p₁ = 3/6 反例 p₂ = 3/6
   D¹(乌黑)={2，3，7，8，9，15} 其中正例p₁ = 4/6 反例 p₂ = 2/6
   D¹(浅白)={5，11，12，14，16} 其中正例p₁ = 1/5 反例 p₂ = 4/5

$$Ent(D^1)=-\sum _{k=1}^2{P}_{k}lo{g}_2{P}_k=-(\frac{3}{6}lo{g}_2\frac{3}{6}+\frac{3}{6}lo{g}_2\frac{3}{6})=1$$
$$Ent(D^2)=-\sum _{k=1}^2{P}_{k}lo{g}_2{P}_k=-(\frac{4}{6}lo{g}_2\frac{4}{6}+\frac{2}{6}lo{g}_2\frac{2}{6})=0.918$$
$$Ent(D^3)=-\sum _{k=1}^2{P}_{k}lo{g}_2{P}_k=-(\frac{1}{5}lo{g}_2\frac{1}{5}+\frac{4}{5}lo{g}_2\frac{4}{5})=0.722$$
由此可得：
$$Gain(D,色泽)=Ent(D)-\sum _{v=1}^3\frac{|D^v|}{|D|}Ent(D^v)=0.109$$

同理：
$$Gain(D,根蒂)=0.143\text{, }Gain(D,敲声)=0.141$$
$$Gain(D,纹理)=0.381\text{, }Gain(D,脐部)=0.289$$
$$Gain(D,触感)=0.006$$

显然，属性纹理的信息增益最大，所以它被选为划分属性

然后决策树算法对每一个分支结点做进一步划分，以纹理=清晰为例，D¹ ={1,2,3,4,5,6,8,10,15}，基于D¹ 计算出各属性的信息增益
$$Gain(D^1,色泽)=0.043\text{, }Gain(D^1,根蒂)=0.458$$
$$Gain(D^1,敲声)=0.331\text{, }Gain(D^1,脐部)=0.458$$
$$Gain(D^1,触感)=0.458$$

不断重复上述步骤，可以得到决策树如下：

增益率

信息增益准则对取值数目较多的属性有所偏好，最极端的理解方式，如果将身份证号作为一个属性，那么，其实每个人的身份证号都是不相同的，也就是说，有多少个人，就有多少种取值，如果用身份证号这个属性去划分原数据集，那么，原数据集中有多少个样本，就会被划分为多少个子集，这样的话，会导致信息增益公式的第二项整体为0，虽然这种划分毫无意义，但是从信息增益准则来讲，这就是最好的划分属性。

为了消除这种影响，使用增益率来划分属性。
$$Gai{n}_{r}atio(D,a)=\frac{Gain(D,a)}{IV(a)}$$
其中$$IV(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}log2\frac{|D^v|}{|D|}$$被称为属性a的固有值，v越大，IV(a)越大

基尼指数

数据D的纯度可用基尼值来衡量，
$$Gini(D)=\sum _{k=1}^{|y|}\sum _{k^1\ne k}{P}_k{P}_{k^1}=1-\sum _{k=1}^{|y|}{P}_k^2$$
表示从D中随机抽取两个样本，他们不一致的概率

而对于属性a的基尼指数,值越小越好。
$$Gini-index(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)$$

剪枝处理

剪枝处理是决策树对付过拟合的主要手段

在决策树学习中，结点的划分过程不断重复，形成的分支过多，产生过拟合。

预剪枝：在决策树生成过程中，在每个结点划分前，先进行评估，若划分不能带来决策树模型泛化能力上的提升，则停止划分，

• 能有效的减少训练时间开销和测试时间开销
• 可能会产生欠拟合

后剪枝：先生成完整的决策树，在自底向上检查，若该结点对应的子树替换成叶结点，能带来决策树泛化能力的提升，则替换之。

连续和缺值

连续值处理

给定样本集D和连续属性a，假定a在D上出现n个不同的取值，将这些值从小到大排序，记为{a₁ ,a₂, … ,a_n}，基于划分点t可将D分为子集D_t^- 和D_t⁺,D_t^-包含那些在属性a上取值不大于t的样本，对于相邻属性取值aⁱ和aⁱ⁺¹, t在区间 [aⁱ，aⁱ⁺¹）上的任何取值划分结果相同，因此，我们选择中位点。
$$T_a=\frac{a^i+a^{i+1}}{2}|1<=i<=n-1$$
so 我们拥有了n-1个可划分取值点。
计算
$$Gain(D,a,t)=ma{x}_{t\in T_a}Ent(D)-\sum _{\lambda \in (-1,+1)}\frac{|D_{T^{\lambda }}|}{|D|}Ent(D_{t^{\lambda }})$$
选择最大取值

缺省值

对于缺省值，我们需要考虑两个问题

• 如何在属性缺失的情况下进行属性选择划分
• 对于划分属性，若样本在该属性上的值缺失，如何对样本进行划分

给定训练集D和属性a，令D_n表示D中在属性a上没有缺省值的样本子集。

对于问题一，假设属性a有v个取值{ a¹ , a², … ,a^v}, 令D_n^v表示D_n中属性a上取值为a^v的样本子集,D_nk表示D_n中属于第k类{k=1，2，…|y|}的样本子集
定义：
$$p=\frac{{\sum }_{x\in D_n}{w}_x}{{\sum }_{x\in D}{w}_x}\text{表}示a中五缺失值样本所占的比例$$
$$p_k=\frac{{\sum }_{x\in D_{n}k}{w}_x}{{\sum }_{x\in D_n}{w}_x}(1<=k<=|y|)\text{表}示无缺失样本中第k类所占的比例$$
$$r_v=\frac{{\sum }_{x\in D_k^v}{w}_x}{{\sum }_{x\in D_n}{w}_x}(1<=v<=V)\text{表}示无缺失样本中a^v所占的比例$$

信息增益可以推广为：
$$Gain(D,a)=p\ast Gain(D_n,a)$$

对于问题2，若样本x在划分属性a上的取值已知，则将x划分到其取值对应的子节点，且样本权值在子节点保持为w_x，若样本x在划分属性a上取值未知，则将x同时划分到所有子节点，且样本权值在于属性a对用的子结点中调整为r_v*w_x

多变量决策树

非叶子结点不再是仅针对某个属性，而是对属性的线性组合进行测试，换言之，每个叶子结点是一个形如${\sum }_{i=1}^d{w}_i{a}_i=t$的线性分类器。