[ABC259D] Circumferences 题解

一、解题思路

本题目细节较多

首先，发现题目要求我们判断可否从 $s$ 点走到 $t$ 点 ，容易想到dfs判连通性

观察数据范围 $1\le N\le 3000$

想到 $n^2$建图，再使用dfs判断连通性

建图是本道题的难点
观察题面，题目说明是圆上的线段相交时才可以移动，不妨将每个圆心抽象为一个点，再通过每两个点的距离与半径的关系判断是否连通

我们知道，两圆之间的关系有5种，分别为相交，外切，外离，内切，内含

其中外离和内含表示两个圆没有公共点
那么剩下三种情况则是合法也就是可以连接两点的情况
画图说明：
当两圆外切时，即两圆的圆心距离等于两圆半径之和时：

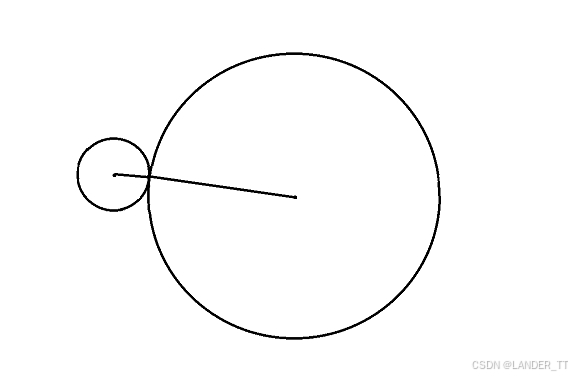
当两圆相交时，即两圆的圆心距离大于两圆半径之差且小于两圆半径之和：

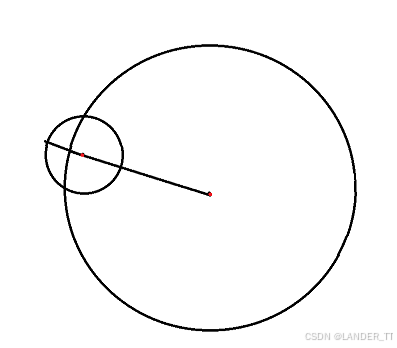
当两圆内切时，即两圆的圆心距离等于两圆半径之差：

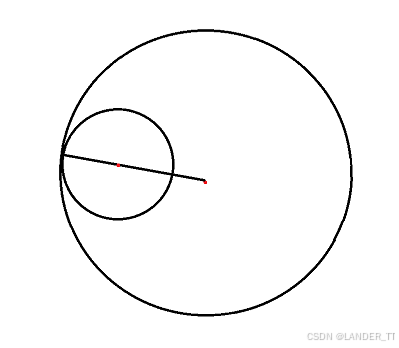
总结规律，发现当圆心距离小于等于半径之和，大于等于半径之差时，两圆上有公共点

令圆心距离为$d$两圆半径分别为$r1,r2$ ，可得出 $|r1-r2|\le d\le |r1+r2|$

接下来就可以建图，使用dfs判连通性跑出结果了

dfs可以直接写简单暴搜，无需剪枝

二、代码展示

#include<bits/stdc++.h>
#define int long long
using namespace std;
struct circle{
	int x,y,r;
}c[200005];
int n,v[200005],sx,sy,tx,ty;
vector<int> e[200005];
int ds(int a,int b){//圆心距离 因为怕掉精度所以整体开了平方
	int x=c[a].x, _x=c[b].x,y=c[a].y,_y=c[b].y;
	return (x-_x)*(x-_x)+(y-_y)*(y-_y);
}
bool ck(int a,int b){//检查两圆是否有交点
	int r1=c[a].r,r2=c[b].r,d=ds(a,b),k1=(r1+r2)*(r1+r2),k2=(r1-r2)*(r1-r2);
	if(d<=k1&&d>=k2)return true;
	return false;
}
void dfs(int s){//dfs判连通性
	if(s==n+1){
		cout<<"Yes";
		exit(0);
	}
	v[s]++;
	if(v[s]>1)return;
	for(auto i:e[s])dfs(i);
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	cin>>n>>c[0].x>>c[0].y>>c[n+1].x>>c[n+1].y;//将起点与终点看作是半径为0的圆
	for(int i=1;i<=n;++i)cin>>c[i].x>>c[i].y>>c[i].r;
	for(int i=0;i<=n+1;++i)
		for(int j=0;j<=n+1;++j)
			if(ck(i,j))
				e[i].push_back(j),
				e[j].push_back(i);
	dfs(0);
	cout<<"No";
	return 0;
}