[LeetCode] 162、寻找峰值

题目描述

峰值元素是指其值大于左右相邻值的元素。

给定一个输入数组 nums，其中 nums[i] ≠ nums[i+1]，找到峰值元素并返回其索引。

数组可能包含多个峰值，在这种情况下，返回任何一个峰值所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞。

你的解法应该是 O(logN) 时间复杂度的。

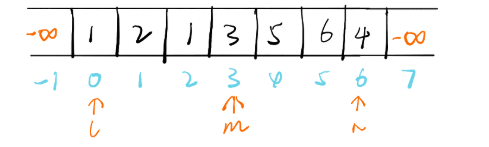
输入: nums = [1,2,1,3,5,6,4]
输出: 1 或 5 
解释: 你的函数可以返回索引 1，其峰值元素为 2；
     或者返回索引 5， 其峰值元素为 6。

解题思路

• 首先要注意题目条件，在题目描述中出现了 nums[-1] = nums[n] = -∞（关键），这就代表着 只要数组中存在一个元素比相邻元素大，那么沿着它一定可以找到一个峰值。 => 我们就可以使用二分查找找到峰值。
• 查找时，左指针 l，右指针 r，以其保持左右顺序为循环条件。
• 根据左右指针计算中间位置 m，并比较 m 与 m+1 的值，如果 m 较大，则左侧存在峰值，r = m，如果 m + 1 较大，则右侧存在峰值，l = m + 1。
  

参考代码

自己代码：（老版的二分代码，需要很多特判才行）

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int length = nums.size();
        if(length == 0)
            return -1;
        if(length == 1)
            return 0;
        
        int low = 0;
        int high = length - 1;
        while(low <= high){
            int mid = (low + high) >> 1;
            
            // 列举了可能是峰值的情况（头、尾、中间），更好理解
            if((mid == 0 && nums[mid] > nums[mid+1]) || (mid == length-1 && nums[mid] > nums[mid-1]) || 
               (mid != 0 && mid != length-1 && nums[mid] > nums[mid-1] && nums[mid] > nums[mid+1])){
                return mid;
            }
            
            if(nums[mid] < nums[mid+1])
                low = mid + 1;
            else
                high = mid;
        }
        
        return -1;
    }
};

精简版：java（推荐）

class Solution {
    public int findPeakElement(int[] nums) {
        int left = 0, right = nums.length - 1;
        while (left < right) {   // 这里是 <
            int mid = left + (right - left) / 2;  // 左中位数
            if (nums[mid] > nums[mid + 1]) {  // mid是左中位数，这保证了mid+1 不会越界（若mid和mid+1比的话，就得用左中位数）
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;  // 由题设，数组一定存在峰值，所以我们能保证最后当 left == right 时一定能返回正确答案
    }
}