排序算法
最近,呕心沥血的学习排序算法,找到了一些动画,来方便总结经典排序算法,不过后期我会继续更新,希望对初学的小伙伴们有帮助哦。
排序算法概述
排序:将一组“无序”的记录序列调整为“有序”的记录序列。
列表排序:将无序列表变为有序列表。
输入:列表
输出:有序列表
升序与降序
内置排序函数:sort()
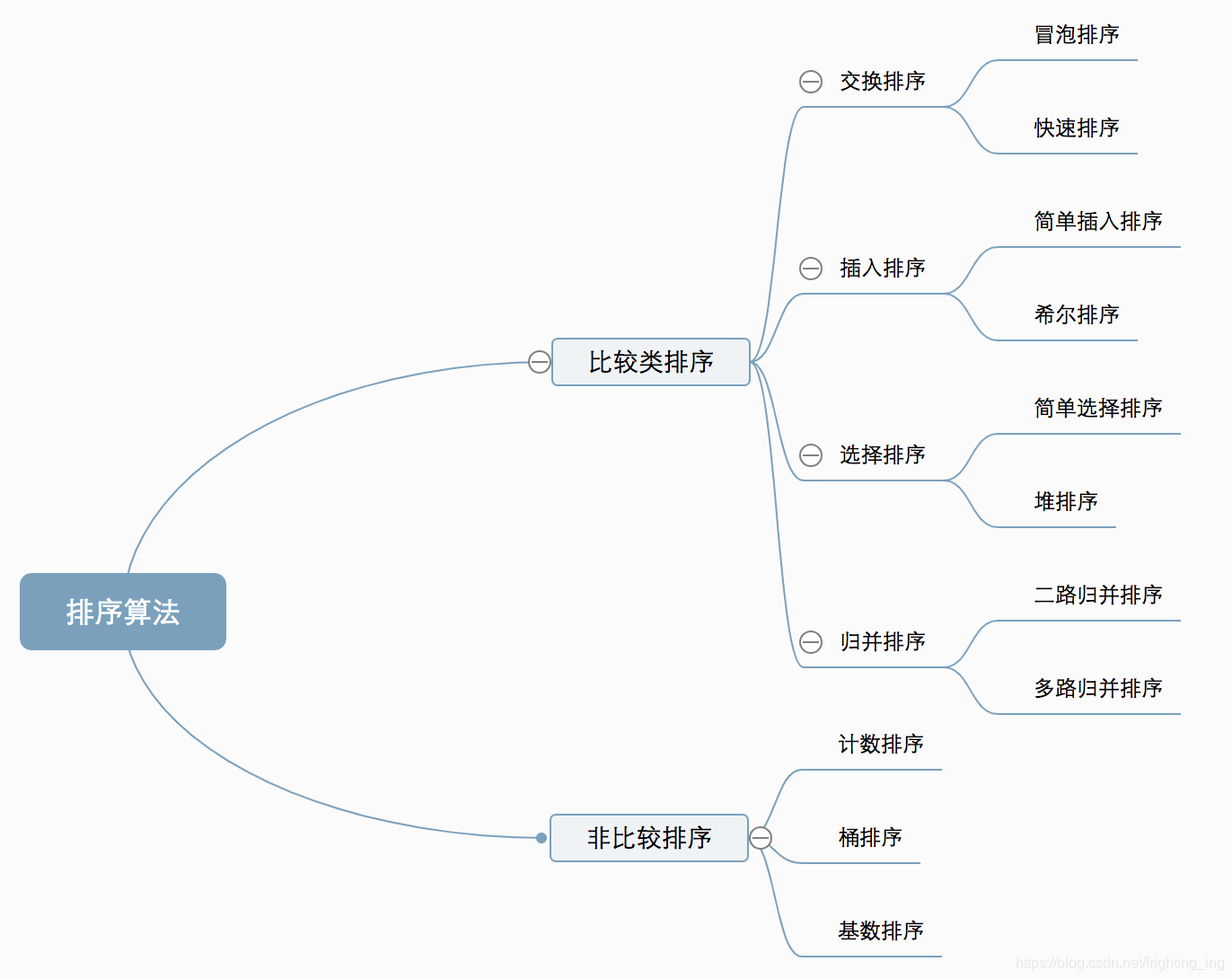
排序方法提纲:

另一种分类方式
全部排序算法的时间复杂度、空间复杂度和稳定性汇总
| 排序算法 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 插入排序 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 |
| 快速排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | O ( l o g n ) O(logn) O(logn) | 不稳定 |
| 堆排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( 1 ) O(1) O(1) | 不稳定 |
| 归并排序 | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n l o g n ) O(nlogn) O(nlogn) | O ( n ) O(n) O(n) | 稳定 |
| 希尔排序 | O ( n 1.5 ) O(n^{1.5}) O(n1.5) | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 计数排序 | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( k ) O(k) O(k) | 稳定 |
| 桶排序 | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( n 2 ) O(n^2) O(n2) | O ( n + k ) O(n+k) O(n+k) | 稳定 |
| 基数排序 | O ( n ∗ k ) O(n*k) O(n∗k) | O ( n ∗ k ) O(n*k) O(n∗k) | O ( n ∗ k ) O(n*k) O(n∗k) | O ( n + k ) O(n+k) O(n+k) | 稳定 |
说明:排序算法的稳定性,指的是排序前后相同元素的相对位置不变,则称排序算法是稳定的;否则排序算法是不稳定的。
下面开始介绍各类算法的实现,例程全部是从小到大排序。
1. 冒泡排序☆☆
原理:它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。把最小的数浮上来,或者把最大的数据沉下去。
列表每两个相邻的数,如果前面比后面大,则交换这两个数。一趟排序完成后,则无序区减少一个数,有序区增加一个数。
动画演示

Python代码实现
def bubble_sort(lis):
for i in range(len(lis)-1):
exchange = False
for j in range(len(lis)-i-1):
if lis[j] > lis[j+1]:
lis[j], lis[j+1] = lis[j+1], lis[j]
exchange = True
if not exchange: # 如果排好了序,也就是一次都不需要继续排序的情况,直接返回
return
return
lis = [3,2,1,4,5]
bubble_sort(lis)
print(lis)
C语言代码实现
#include <stdio.h>
void bubble_sort(int* arr, int len) //升序
{
int i, j;
int temp;
for (i = 0; i < len - 1; i++ )
{
for (j = 0; j < len - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main(void)
{
int arr[5] = { 2,5,1,3,4 };
int num = sizeof(arr) / sizeof(arr[0]);
bubble_sort(arr, num);
for (int i = 0; i < num; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
C++语言代码实现
#include <iostream>
using namespace std;
void bubble_sort(int pArr[], int length)
{
for (int i = 0; i < length - 1; i++)
{
bool exchange = false;
for (int j = 0; j < length - 1 - i; j++)
{
if (pArr[j] > pArr[j + 1])
{
int temp = pArr[j];
pArr[j] = pArr[j + 1];
pArr[j + 1] = temp;
exchange = true;
}
}
if (!exchange)
{
return;
}
}
return;
}
int main(void)
{
int arr[] = { 2, 5, 1, 3, 4 };
int length = sizeof(arr) / sizeof(arr[0]);
bubble_sort(arr, length);
for (int i = 0; i < length; i++)
{
cout << arr[i] << ' ';
}
cout << endl;
system("pause");
return 0;
}
2. 选择排序☆☆
原理:选择排序和冒泡很像,它也是比较两个元素,不过它先不交换,等到选取最大或者最小的数据之后再进行交换。
一趟排序记录最小的数,放到第一个位置,在一趟排序记录记录列表无序区最小的数,放到第二个位置。
动画演示

Python代码实现
def select_sort(lis):
for i in range(len(lis)-1):
min_num = i
for j in range(i+1, len(lis)):
if lis[min_num] > lis[j]:
min_num = j
if min_num != i:
lis[i], lis[min_num] = lis[min_num], lis[i]
return
lis = [3,2,5,4,6,8]
print(lis)
select_sort(lis)
print(lis)
C语言代码实现
#include <stdio.h>
void select_sort(int* arr, int len)
{
int i, j, min;
int temp;
for (i = 0; i < len - 1; i++)
{
for (min = i, j = i + 1; j < len; j++)
{
if (arr[min] > arr[j])
{
min = j;
}
}
if (min != i)
{
temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}
}
int main(void)
{
int arr[5] = { 2,5,1,3,4 };
int num = sizeof(arr) / sizeof(arr[0]);
select_sort(arr, num);
for (int i = 0; i < num; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
C++语言代码实现
#include <iostream>
using namespace std;
void select_sort(int pArr[], int length)
{
int i, j;
int ind_min;
for (i = 0; i < length - 1; i++)
{
ind_min = i;
for (j = i + 1; j < length; j++)
{
if (pArr[ind_min] > pArr[j])
ind_min = j;
}
if (ind_min != i)
{
int temp = pArr[ind_min];
pArr[ind_min] = pArr[i];
pArr[i] = temp;
}
}
for (int i = 0; i < length; i++)
{
cout << pArr[i] << ' ';
}
cout << endl;
}
int main(void)
{
int arr[] = { 2, 5, 6, 3, 4 };
int length = sizeof(arr) / sizeof(arr[0]);
select_sort(arr, length, 0, 4);
for (int i = 0; i < length; i++)
{
cout << arr[i] << ' ';
}
cout << endl;
system("pause");
return 0;
}
3. 插入排序☆☆☆
原理:从第二位数据开始, 当前数(第一趟是第二位数)与前面的数依次比较,如果前面的数大于当前数,则将这个数放在当前数的位置上,当前数的下标-1,直到当前数不大于前面的某一个数为止。直到遍历至最后一位元素。
通俗的讲,就是从第二位开始,更小的值往前插入。前面的数据肯定是插入排序已经排列好的,前面的值小于或等于当前值基准值的位置。
初始时手里(有序区)只有一张牌,每次(从无序区)摸一张牌,插入到手里已有牌的正确位置。

动画演示

Python代码实现
def insert_sort(lis):
for i in range(1, len(lis)):
temp = lis[i] # 摸到的牌
j = i - 1 # 指的是手里面的牌
while lis[j] > temp and j >= 0:
lis[j+1] = lis[j]
j -= 1
lis[j+1] = temp
lis = [3,2,4,1,5]
insert_sort(lis)
print(lis)
C语言代码实现
#include <stdio.h>
void insert_sort(int* arr, int len)
{
int i, j;
int temp;
for (i = 1; i < len; i++)
{
temp = arr[i]; // 把手里的牌拿出来
j = i - 1;
while (arr[j] > temp && j >= 0)
{
arr[j + 1] = arr[j];
j--;
}
arr[j+1] = temp;
}
}
int main(void)
{
int arr[5] = { 2,5,1,3,4 };
int num = sizeof(arr) / sizeof(arr[0]);
insert_sort(arr, num);
for (int i = 0; i < num; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
return 0;
}
C++语言代码实现
#include <iostream>
using namespace std;
void insert_sort(int pArr[], int length)
{
int i, j;
for (i = 1; i < length; i++)
{
int obj = pArr[i];
j = i - 1;
while (j >= 0 && pArr[j] > obj)
{
pArr[j + 1] = pArr[j];
j--;
}
pArr[j + 1] = obj;
}
return;
}
int main(void)
{
int arr[] = { 2, 5, 6, 3, 4 };
int length = sizeof(arr) / sizeof(arr[0]);
insert_sort(arr, length);
for (int i = 0; i < length; i++)
{
cout << arr[i] << ' ';
}
cout << endl;
system("pause");
return 0;
}
4. 快速排序☆☆☆☆☆
原理:通过一趟排序将序列分成左右两部分,其中左半部分的的值均比右半部分的值小,然后再分别对左右部分的记录进行排序,直到整个序列有序。
快速排序思路:
- 取一个元素p(第一个元素),使元素p归为;
- 列表被p分成两部分,左边都比p小,右边都比p大;
- 递归完成排序。
动画演示



Python代码实现
def quick_sort(lis, left, right):
if left < right:
mid = partition(lis, left, right)
quick_sort(lis, left, mid-1)
quick_sort(lis, mid+1, right)
def partition(lis, left, right):
temp = lis[left]
while left < right:
while left < right and lis[right] >= temp:
right -= 1
lis[left] = lis[right]
while left < right and lis[left] <= temp:
left += 1
lis[right] = lis[left]
lis[left] = temp
return left
lis = [3,5,2,5,6,7,1]
quick_sort(lis, 0, len(lis)-1)
print(lis)
C语言代码实现
#include <stdio.h>
int FindPos(int* a, int low, int high)
{
int val = a[low];
while (low < high)
{
while (low < high && a[high] >= val)
{
--high;
}
a[low] = a[high];
while (low < high && a[low] <= val)
{
++low;
}
a[high] = a[low];
}
a[low] = val;
return low;
}
void Quick_sort(int* a, int low, int high)
{
int pos;
if (low < high)
{
pos = FindPos(a, low, high);
Quick_sort(a, low, pos-1);
Quick_sort(a, pos + 1, high);
}
}
int main(void)
{
int a[6] = { 2,3,1,7,6,5 };
int i;
Quick_sort(a, 0, 5);
for (int i = 0; i < 6; i++)
{
printf("%d ", a[i]);
}
printf("\n");
return 0;
}
C++语言代码实现
#include <iostream>
using namespace std;
int quick(int pArr[], int len, int left, int right)
{
int obj = pArr[left];
while (left < right)
{
while (left < right && pArr[right] >= obj)
right--;
pArr[left] = pArr[right];
while (left < right && pArr[left] <= obj)
left++;
pArr[right] = pArr[left];
}
pArr[left] = obj;
return left;
}
void quick_sort(int pArr[], int len, int left, int right)
{
if (left < right)
{
int mid = quick(pArr, len, left, right);
quick_sort(pArr, len, left, mid-1);
quick_sort(pArr, len, mid + 1, right);
}
}
int main(void)
{
int arr[] = { 2, 5, 6, 3, 4 };
int length = sizeof(arr) / sizeof(arr[0]);
quick_sort(arr, length);
for (int i = 0; i < length; i++)
{
cout << arr[i] << ' ';
}
cout << endl;
system("pause");
return 0;
}
topK:
def quickK(nums, left, right, k):
i, j = left, right
num = nums[left]
while i < j:
while i < j and nums[j] <= num:
j -= 1
nums[i] = nums[j]
while i < j and nums[i] >= num:
i += 1
nums[j] = nums[i]
nums[i] = num
if i == k-1:
return
else:
if j >= k:
quickK(nums, left, i-1, k)
else:
quickK(nums, i+1, right, k)
return
5. 堆排序☆☆☆☆
堆排序是指利用堆这种数据结构所设计的一种排序算法。利用了堆的一个总要性质,即子结点的键值或索引总是小于(或者大于)它的父节点。
内容补充:
树是一种数据结构,比如:目录结构
树是一种可以递归定义的数据结构
数是由n个节点组成的集合:
- 如果n=0,那这是一棵空树;
- 如果n>0,那存在1个节点作为数的根节点,其他节点可以分为m个结合,每个集合本身又是一棵树。
一些概念:
- 根节点;叶子节点(不能再分)
- 树的深度(高度)树的高度和深度以及结点的高度和深度_LolitaSian-优快云博客_树的深度
- 树的度(最多向下分的叉)
- 孩子节点/父节点
- 子树
二叉树
- 度不超过2的数
- 每个节点最多有两个孩子节点
- 两个孩子节点被区分为左孩子节点和右孩子节点
满二叉树
- 一个二叉树,如果每一个层的节点数都达到最大值,则这个二叉树就是满二叉树
完全二叉树:
- 叶节点只能出现在最下层和词下层,并且最下面一层的节点都集中在该层最左边的若干位置的二叉树

二叉树的存储方法(表示方法)
- 链式存储方法
- 顺序存储方法
顺序存储方法
- 列表

父节点和左孩子节点编号下标关系:
i==>2i+1 从父节点==>左子节点
父节点和右孩子节点编号下标关系:
i==>2i+2 从父节点==>右子节点
孩子节点和父亲节点编号下标关系:
i==>(i-1)//2 从子节点==>父节点
堆:一种特殊的完全二叉树结构
- 大根堆:一颗完全二叉树,满足任一节点都比其孩子节点大
- 小根堆:一颗完全二叉树,满足任一节点都比其孩子节点小

堆的向下调整
- 假设根节点的左右子树都是堆,但根节点不满足堆的性质
- 当根节点的左右子树都是堆时,可以通过一次向下的调整来将其变换成一个堆
堆排序的过程
- 建立一个堆(从最后一个非叶子节点向下调整,直至最后一个非叶子节点)
- 得到堆顶元素,为最大元素
- 去掉堆顶,为堆最后一个元素放到堆顶
- 堆顶元素为第二大元素
- 重复步骤3,直到堆变空
堆排序原理:从小到大排序,则使用大顶堆,每次取堆顶元素和后面的元素交换,然后对剩下的元素进行大顶堆排序。
堆排序:topk问题
- 现在有n个数,设计算法得到前k大的数。(k<n)
- 解决思路:
- 排序后切片( O ( n l o g n ) O(nlogn) O(nlogn)+k) 可舍去k
- 冒泡,插入,选择排序( O ( k n ) O(kn) O(kn))
- 堆排序思路,
O
(
n
l
o
g
k
)
O(nlogk)
O(nlogk)
- 取列表前k个元素建立一个小根堆。堆顶就是目前第k大的数
- 依次向后遍历原列表,对于列表中的元素,如果小于堆顶,则 忽略该元素;如果大于堆顶,则将堆顶更换为该元素,并且堆堆继进行依次调整;
- 遍历列表所有元素后,倒序弹出堆顶
动画演示


Python代码实现
# 堆排序 --- 最难
def sift(lis, low, high):
'''
:param lis: 列表
:param low: 堆的根节点位置
:param high: 堆的最后一个元素位置
:return:
'''
i = low # i最开始指向根节点,整个过程是指父类
j = 2*i + 1 # 左孩子
tmp = lis[i] # 把堆顶存起来
while j <= high:
if j+1 <= high and lis[j+1] > lis[j]: # 如果右孩子有并且比较大
j = j + 1 # j指向右孩子
if lis[j] > tmp:
lis[i], lis[j] = lis[j], lis[i]
i = j # 往下看一层
j = 2*i + 1
else: # tmp更大,把tmp放到某一领导位置
break
def heap_sort(lis):
n = len(lis)
for i in range((n-2)//2, -1, -1):
# i表示建堆的时候调整的部分的根的下标:
sift(lis, i, n-1)
# 建堆完成了
for i in range(n-1, -1, -1):
# i 指向当前堆的最后一个元素
lis[0] ,lis[i] = lis[i], lis[0]
sift(lis, 0, i - 1) # i-1是新的high
lis = list(range(100))
import random
random.shuffle(lis)
heap_sort(lis)
print(lis)
heap_sort(lis)
内置模块
# ---------------------------------系统内置堆排序-----------------------------------
import heapq # queue 优先队列
import random
li = list(range(100))
random.shuffle(li)
print(li)
heapq.heapify(li) # 建堆
print(li)
n = len(li)
for i in range(n):
print(heapq.heappop(li), end=',')
C++代码实现
#include <iostream>
using namespace std;
//堆排序
void sift(int arr[], int len, int low, int high)
{
int i = low;
int j = 2 * i + 1;
while (j <= high)
{
if (j + 1 <= high && arr[j + 1] > arr[j])
j = j + 1;
if (arr[j] > arr[i])
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
cout << i << j << endl;
i = j;
j = 2 * i + 1;
cout << i << j << endl;
}
else
break;
}
}
void heap_sort(int arr[], int len)
{
for (int i = ((len - 2) / 2); i >= 0; i--)
{
sift(arr, len, i, len - 1);
}
for (int j = len - 1; j >= 0; j--)
{
int temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
sift(arr, len, 0, j - 1);
}
}
int main(void)
{
int arr[] = { 1, 2, 5, 4, 3 };
int len = sizeof(arr) / sizeof(arr[0]);
heap_sort(arr, len);
display(arr, len);
system("pause");
return 0;
}
STLvector版本
#include<iostream>
using namespace std;
#include<vector>
//建立小根堆
void sift(vector<int>& vec, int low, int high) {
int i = low; // ge
int j = 2 * i + 1;
while (j <= high) {
if (j + 1 <= high && vec[j + 1] > vec[j]) j++;
if (vec[j] > vec[i]) {
swap(vec[j], vec[i]);
i = j;
j = 2 * i + 1;
}
else {
break;
}
}
}
void heapSort(vector<int>& vec) {
int len = vec.size();
for (int i = (len - 2) / 2; i >= 0; i--) {
sift(vec, i, len - 1);
}
for (int j = len - 1; j >= 0; j--) {
swap(vec[0], vec[j]);
sift(vec, 0, j - 1);
}
}
void test01() {
vector<int> vec{ 2,5,4,3,1 };
heapSort(vec);
for (int i : vec) {
cout << i << " ";
}
cout << endl;
}
int main() {
test01();
system("pause");
return 0;
}
priority_queue优先级队列的原理就是堆排序
Problem:现在有n个数,设计算法得到前k大的数。(k<n)
解决思路:
- 排序后切片( O ( n l o g n ) O(nlogn) O(nlogn)+k) 可舍去k
- 冒泡,插入,选择排序( O ( k n ) O(kn) O(kn))
- 堆排序思路,
O
(
n
l
o
g
k
)
O(nlogk)
O(nlogk)
- 取列表前k个元素建立一个小根堆。堆顶就是目前第k大的数
- 依次向后遍历原列表,对于列表中的元素,如果小于堆顶,则 忽略该元素;如果大于堆顶,则将堆顶更换为该元素,并且堆堆继进行依次调整;
- 遍历列表所有元素后,倒序弹出堆顶
Python代码实现
# 小根堆
def sift(lis, low, high):
'''
:param lis: 列表
:param low: 堆的根节点位置
:param high: 堆的最后一个元素位置
:return:
'''
i = low # i最开始指向根节点,整个过程是指父类
j = 2*i + 1 # 左孩子
tmp = lis[i] # 把堆顶存起来
while j <= high:
if j+1 <= high and lis[j+1] < lis[j]: # 如果右孩子有并且比较大
j = j + 1 # j指向右孩子
if lis[j] < tmp:
lis[i] = lis[j]
i = j # 往下看一层
j = 2*i + 1
else: # tmp更大,把tmp放到某一领导位置
break
lis[i] = tmp # 把tmp放到叶子节点上
def topk(li, k):
# 1. 建堆K小堆
for i in range((k-2)//2, -1, -1):
sift(li, i, k-1)
# 2. 更新K小堆,0对应元素为堆中最小值
for i in range(k, len(li)-1):
if li[i] > heap[0]:
heap[0] = li[i]
sift(li, 0, k-1)
return li[0]
import random
li = list(range(1000))
random.shuffle(li)
print(topk(li,10))
6. 归并排序(额外开辟空间)☆☆☆☆☆
归并排序是把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。



Python代码实现
def merge(lis, low, mid, high):
i = low
j = mid + 1
temp = []
while i <= mid and j <= high:
if lis[i] < lis[j]:
temp.append(lis[i])
i += 1
else:
temp.append(lis[j])
j += 1
while i <= mid:
temp.append(lis[i])
i += 1
while j <= high:
temp.append(lis[j])
j += 1
lis[low: high+1] = temp
def merge_sort(lis, low, high):
if low < high:
mid = (low + high) // 2
merge_sort(lis, low, mid)
merge_sort(lis, mid+1, high)
merge(lis, low, mid, high)
lis = [2,4,6,7,1,3,5,8]
merge_sort(lis, 0, 7)
print(lis)
C++语言代码实现
#include <iostream>
using namespace std;
void merge(int pArr[], int len, int left, int mid, int right)
{
int i = left;
int j = mid + 1;
int ind = 0;
int *temp = new int[right - left + 1];
while (i <= mid && j <= right)
{
if (pArr[i] < pArr[j])
{
temp[ind++] = pArr[i++];
}
else
{
temp[ind++] = pArr[j++];
}
}
while (i <= mid)
{
temp[ind++] = pArr[i++];
}
while (j <= right)
{
temp[ind++] = pArr[j++];
}
for (int k = 0; k <= ind; k++)
{
pArr[left + k] = temp[k];
}
delete[] temp;
}
void merge_sort(int pArr[], int len, int left, int right)
{
if (left < right)
{
int mid = (left + right) / 2;
merge_sort(pArr, len, left, mid);
merge_sort(pArr, len, mid + 1, right);
merge(pArr, len, left, mid, right);
}
}
int main(void)
{
int arr[] = { 2, 5, 6, 3, 4 };
int length = sizeof(arr) / sizeof(arr[0]);
merge_sort(arr, length);
for (int i = 0; i < length; i++)
{
cout << arr[i] << ' ';
}
cout << endl;
system("pause");
return 0;
}
小总结:快速排序、堆排序和归并排序
三种排序算法的时间复杂度都是 O ( n l o g n ) O(nlogn) O(nlogn)
一般情况下,就运行时间而言:
- 快速排序<归并排序<堆排序
三种排序算法的缺点:
- 快速排序:极端情况下排序效率低
- 归并排序:需要额外的内存开销
- 堆排序:在快的排序算法中相对较慢
7. 希尔排序☆
原理:希尔排序是插入排序改良的算法,是插入排序的一种高效率的实现,也叫缩小增量排序。希尔排序步长从大到小调整,所以步长是关键,最终步长为1,做最后的排序。
步长为1的时候肯定能排出符合的序列。
希尔排序是插入排序的变形,希尔排序是一种分组插入排序算法
实现步骤如下:
- 首先取一个整数 d 1 = n / 2 d_1=n/2 d1=n/2,将元素分为 d 1 d_1 d1个组,每组相邻量元素之间距离为 d 1 d_1 d1,在各组内进行直接插入排序
- 取第二个整数 d 2 = d 1 / 2 d_2=d_1/2 d2=d1/2,重复上述分组排序过程,直到 d i = 1 d_i=1 di=1,即所有元素在同一组内进行直接插入排序
- 希尔排序每趟并不使某些元素有序,而是使整体数据越来越接近有序;最后一趟排序使得所有数据有序
希尔排序速度低于堆排序(NB三人组)
gap的选择不同,时间复杂度不同(目前仍有大佬在研究)
动画演示


Python代码实现
def insert_sort_gap(lis, gap): # 将插入排序中的1改为gap即可
for i in range(len(lis)):
temp = lis[i]
j = i - gap
while j >= 0 and lis[j] > temp:
lis[j+gap] = lis[j]
j -= gap
lis[j+gap] = temp
def shell_sort(lis):
d = len(lis) // 2
while d >= 1:
insert_sort_gap(lis, d)
d //= 2
lis = [3,1,2,4,5,7,6]
shell_sort(lis)
print(lis)
C++代码实现
#inlcude <iostream>
using namespace std;
void insert_sort_gap(int arr[], int len, int gap)
{
for (int i = 1; i < len; i += gap)
{
int val = arr[i];
int j = i - gap;
while (j >= 0 && arr[j] > val)
{
lis[j+gap] = lis[j];
j -= gap;
}
lis[j+gap] = val;
}
}
void shell_sort(int arr[], int len)
{
int d = len / 2;
while (d >= 1)
{
insert_sort_gap(arr, len, d);
d /= 2;
}
}
int main(void)
{
int arr[] = { 2, 5, 4, 3, 1 };
int len = sizeof(arr) / sizeof(arr[0]);
shell_sort(arr, len);
for (int i = 0; i < len; i++)
{
cout << arr[i] << endl;
}
}
希尔排序比较于插入排序
希尔排序的时间性能优于直接插入排序的原因:
①当文件初态基本有序时直接插入排序所需的比较和移动次数均较少。
②当n值较小时,n和
n
2
n^2
n2的差别也较小,即直接插入排序的最好时间复杂度O(n)和最坏时间复杂度O(
n
2
n^2
n2)差别不大。
③在希尔排序开始时增量较大,分组较多,每组的记录数目少,故各组内直接插入较快,后来增量di逐渐缩小,分组数逐渐减少,而各组的记录数目逐渐增多,但由于已经按di-1作为距离排过序,使文件较接近于有序状态,所以新的一趟排序过程也较快。
因此,希尔排序在效率上较直接插入排序有较大的改进。
8. 计数排序(额外开辟空间)☆☆
原理:当待排序的数的值都是在一定的范围内的整数时,可以用待排序的数作为计数数组的下标,统计每个数的个数,然后依次输出即可。
算法步骤:
- 花O(n)的时间扫描一下整个序列 A,找出序列的最大值:max
- 开辟一块新的空间创建新的数组 B,长度为 ( max + 1)
- 数组 B 中 index 的元素记录的值是 A 中某元素出现的次数
- 最后输出目标整数序列,具体的逻辑是遍历数组 B,输出相应元素以及对应的个数
对列表进行排序,已知列表中的数范围都在0到100之间。设计时间复杂度为 O ( n ) O(n) O(n)的算法
速度很快,快于系统的排序,但局限性较多,如,需要使用额外空间内存,最大数字不一定清楚,存在小数无法解决等问题
动画演示
Python代码实现
def count_sort(lis, max_count = 100):
count = [0 for _ in range(max_count + 1)]
for val in lis:
count[val] += 1
lis.clear()
# 方法1
for ind, val in enumerate(count):
for _ in range(val):
lis.append(ind)
# 方法 2
# for j in range(max_count+1):
# while count[j] > 0:
# lis.append(j)
# count[j] -= 1
import random
lis = [random.randint(0, 100) for _ in range(1000)]
count_sort(lis)
print(lis)
C++代码实现
#include <iostream>
using namespace std;
void count_sort(int arr[], int len, int max)
{
int *parr = new int[max + 1]();
for (int i = 0; i < len; i++)
{
parr[arr[i]]++;
}
int index = 0;
for (int j = 0; j < max+1; j++)
{
while (parr[j] != 0)
{
arr[index++] = j;
parr[j]--;
}
}
}
int main(void)
{
int arr[] = { 3, 2, 5, 2, 1, 4, 5, 2, 3 };
int len = sizeof(arr) / sizeof(arr[0]);
count_sort(arr, len1, 5);
for (int i = 0; i < len; i++)
{
cout << arr[i] << " ";
}
cout << endl;
}
def count_sort(nums):
min_num, max_num = min(nums), max(nums)
temp = [0] * (max_num-min_num+1)
for num in nums:
temp[num-min_num] += 1
index = 0
for i, n in enumerate(temp):
for _ in range(n):
nums[index] = i+min_num
index += 1
return
9. 桶排序(额外开辟空间)☆
桶排序改造计数排序
桶排序:首先将元素分在不同的桶中,在对每个桶中的元素排序。
桶排序的表现取决于数据的分布,也就是需要对不同数据排序时采取不同的分桶策略
图片演示



Python代码实现
提前提供桶
def bucket_sort(lis, n=100, max_num=10000):
buckets = [[] for _ in range(n)] # 创建桶
for var in lis:
i = min(var // (max_num // n), n-1) # i表示var放到几号桶里
buckets[i].append(var) # 把var加到桶里面
# 保持桶内的顺序,进行排序
for j in range(len(buckets[i])-1, 0, -1):
if buckets[i][j-1] > buckets[i][j]:
buckets[i][j-1], buckets[i][j] = buckets[i][j], buckets[i][j-1]
else:
break
sorted_lis = []
for buc in buckets:
sorted_lis.extend(buc)
return sorted_lis
import random
lis = [random.randint(0,10000) for _ in range(1000)]
print(bucket_sort(lis))
C++代码实现
注:在我看了很多关于桶排序的C++代码时,发现大家写的要么时计数排序要么就是难以看的代码,为了方便大家看,我注释了一下,如果看不懂的地方直接评论哦
#include <iostream>
using namespace std;
#include <algorithm>
#include <vector>
void bucket(int arr[], int len, int n = 10, int max_count = 100)
{
vector<vector<int>> buckets(n); // 创建桶
for (int i = 0; i < len; i++)
{
int val = min(arr[i] / (max_count / n), n - 1); //确定元素属于那个桶
buckets[val].push_back(arr[i]); // 放入桶
for (int j = buckets[val].size() - 1; j > 0; j--) // 对放入新元素的桶进行排序
{
if (buckets[val][j - 1] > buckets[val][j])
{
int temp = buckets[val][j - 1];
buckets[val][j - 1] = buckets[val][j];
buckets[val][j] = temp;
}
}
}
int index = 0;
for (int k = 0; k < n; k++) // 将桶内元素返回到arr中
{
for (int l = 0; l < buckets[k].size(); l++)
{
arr[index++] = buckets[k][l];
}
}
return;
}
int main(void)
{
int arr[] = { 1, 9, 3 , 2, 15, 20, 30, 50, 41, 31 };
int len = sizeof(arr) / sizeof(arr[0]);
bucket(arr, len, 5, 50);
for (int i = 0; i < len; i++)
cout << arr[i] << " ";
cout << endl;
system("pause");
return 0;
}
自动计算桶(仅差别两处)
def bucket_sort(nums):
maxNum = max(nums)
minNum = min(nums)
n = max((maxNum - minNum) // len(nums), 1) # 注意差别1
buckets = [[] for _ in range(n)]
for num in nums:
i = min((num - minNum) // n, n-1) # 注意差别2
buckets[i].append(num)
for j in range(len(buckets[i])-1, 0, -1):
if buckets[i][j-1] > buckets[i][j]:
buckets[i][j-1], buckets[i][j] = buckets[i][j], buckets[i][j-1]
else:
break
index = 0
for bucket in buckets:
for n in bucket:
nums[index] = n
index += 1
return
#include <iostream>
using namespace std;
#include <algorithm>
#include <vector>
void bucket(vector<int>& nums)
{
int maxNum = *max_element(nums.begin(), nums.end());
int minNum = *min_element(nums.begin(), nums.end());
int n = (maxNum - minNum) / nums.size();
vector<vector<int>> buckets(n); // 创建桶
for (int num : nums)
{
int val = min((num - minNum) / n, n - 1); //确定元素属于那个桶
buckets[val].push_back(num); // 放入桶
for (int j = buckets[val].size() - 1; j > 0; j--) // 对放入新元素的桶进行排序
{
if (buckets[val][j - 1] > buckets[val][j])
{
int temp = buckets[val][j - 1];
buckets[val][j - 1] = buckets[val][j];
buckets[val][j] = temp;
}
}
}
int index = 0;
for (vector<int>& bucket : buckets) {
for (int n : bucket) {
nums[index++] = n;
}
}
return;
}
int main(void)
{
vector<int> nums = { 1, 9, 3 , 2, 15, 20, 30, 50, 41, 31 };
bucket(nums);
for (int n : nums)
cout << arr[i] << " ";
cout << endl;
system("pause");
return 0;
}
10. 基数排序(额外开辟空间)☆
多关键字排序:加入现在有一个员工表,要求按照薪资排序,年龄相同的员工按照年龄排序。
- 先按照年龄进行排序,再按照薪资进行稳定的排序
对32,13,94,52,17,54,91排序,是否可以看作多关键字排序
对下列数字进行排序,按照多关键字进行排序:
- 以个位数数字大小进行类似分桶操作
- 按照分桶的顺序排序,能保证十位数排序时直接按排序结果出数
- 按照十位进行分桶
- 把桶里的数逐一放出来
动画演示


Python代码实现
def radix_sort(li):
max_num = max(li) # 最大值
it = 0
while 10 ** it <= max_num:
buckets = [[] for _ in range(10)] # 创建10个桶
for val in li:
digit = (val // 10 ** it) % 10 # 看现在区分的位数
buckets[digit].append(val)
# 分桶完成
li.clear()
for buc in buckets:
li.extend(buc)
# 把数重新写回li
it += 1
import random
li = list(range(1000))
random.shuffle(li)
radix_sort(li)
print(li)
C++
#include <iostream>
using namespace std;
#include <algorithm>
#include <vector>
int max_arr(int arr[], int len)
{
int max_num = 0;
for (int i = 1; i < len; i++)
{
if (arr[max_num] < arr[i])
max_num = i;
}
return arr[max_num];
}
void radix_sort(int arr[], int len)
{
int it = 0;
int max_num = max_arr(arr, len);
while (pow(10, it) <= max_num)
{
vector<vector<int>> buckets(10);
for (int i = 0; i < len; i++)
{
int val = (arr[i] / pow(10, it));
val %= 10;
buckets[val].push_back(arr[i]);
for (int j = buckets[val].size() - 1; j > 0; j--)
{
if (buckets[val][j - 1] > buckets[val][j])
{
int temp = buckets[val][j - 1];
buckets[val][j - 1] = buckets[val][j];
buckets[val][j] = temp;
}
}
}
int index = 0;
for (int k = 0; k < 10; k++)
{
for (int l = 0; l < buckets[k].size(); l++)
{
arr[index++] = buckets[k][l];
}
}
it++;
}
return;
}
int main(void)
{
int arr[] = { 1, 9, 3, 2, 15, 20, 30, 50, 41, 31 };
int len = sizeof(arr) / sizeof(arr[0]);
radix_sort(arr, len);
for (int i = 0; i < len; i++)
cout << arr[i] << " ";
cout << endl;
system("pause");
return 0;
}
总结
十大经典算法的各难易程度不同,在学习过程中,不但应该掌握基本的原理,同时也应该自己手敲代码,如果有能力可以将上述的代码进行一定程度的改进,相信你会有很大的收获。
各种排序方法的综合比较
一、时间性能
- 按平均的时间性能来分,有三类排序方法:
- 时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)的方法有:快速排序、归并排序、堆排序
- 时间复杂度为 O ( n 2 ) O(n^2) O(n2)的有:冒泡排序、选择排序、插入排序
- 时间复杂度为 O ( n ) O(n) O(n)的有:计数排序、桶排序、基数排序
-
当待排记录序列按关键字顺序有序时,冒泡排序和插入排序能达到 O ( n ) O(n) O(n)的时间复杂度;而对于快速排序而言,这事最不好的情况,此时的时间性能退化为 O ( n 2 ) O(n^2) O(n2),因此是应该尽量避免的情况。
-
选择排序、堆排序和归并排序的时间性能不随记录序列中关键字的分布而改变
二、空间性能
指的是排序过程中所需的辅助空间大小
- 所有的简单排序方法(包括:插入排序、冒泡排序和选择排序)和堆排序的空间复杂度为 O ( 1 ) O(1) O(1)
- 快速排序为 O ( l o g n ) O(logn) O(logn),为栈所需的辅助空间
- 归并排序所需辅助空间最多,其空间复杂度为 O ( n ) O(n) O(n)
- 链式基数排序需附设队列首尾指针,则空间复杂度为 O ( r d ) O(rd) O(rd)
三、排序方法的稳定性能
- 稳定的排序方法指的是,对于两个关键字相等的记录,它们在序列中的相对位置,在排序之前和经过排序之后,没有改变。
- 当对多关键字的记录序列进行LSD方法排序时,必须采用稳定的排序方法。
- 对于不稳定排序的排序方法,只要能举出一个实例说明即可。
- 快速排序和堆排序是不稳定的排序方法。
四、关于”排序方法的时间复杂度的下限“
- 除基数排序外,其它方法都是基于”比较关键字“进行排序的排序方法,可以证明,这类排序方法可能到达的最快的时间复杂度为
O
(
n
l
o
n
g
)
O(nlong)
O(nlong)。
(基础排序不是基于”比较关键字“的排序方法,所以它不受这个限制。) - 可以用一棵判定树来描述这类基于”比较关键字“进行排序的排序方法。








 本文详细介绍了十大经典排序算法,包括冒泡排序、选择排序、插入排序、快速排序、堆排序、归并排序、希尔排序、计数排序、桶排序和基数排序。对每种排序算法的原理、时间复杂度、空间复杂度和稳定性进行了分析,并提供了Python、C和C++的代码实现。这些排序算法在不同的场景下有不同的优劣,理解和掌握它们对于优化算法性能至关重要。
本文详细介绍了十大经典排序算法,包括冒泡排序、选择排序、插入排序、快速排序、堆排序、归并排序、希尔排序、计数排序、桶排序和基数排序。对每种排序算法的原理、时间复杂度、空间复杂度和稳定性进行了分析,并提供了Python、C和C++的代码实现。这些排序算法在不同的场景下有不同的优劣,理解和掌握它们对于优化算法性能至关重要。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










